一、语法和语义
什么是语法?
程序本质上是一定字符集上的字符串,这些字符串描述了一定数据的处理过程,语法规则和词法规则定义了程序的形式结构。所以呢,
语法就是一组规则,用它可以形成和产生一个合式(well-formed)的程序。
词法规则:单词符号的形成规则
- 单词符号是语言中具有独立意义的最基本结构,一般包括:常数、标识符、基本字、算符、界符等。
- 描述工具:有限自动机
语法规则:语法单位的形成规则
- 语法单位通常包括:表达式、语句、分程序、过程、函数、程序等。
- 描述工具:上下文无关文法
什么是语义?
语义同样也是是一组规则,用它可以定义一个程序的意义。描述语义的方法有自然语言描述和形式描述,但自然语言描述具有二义性、隐藏错误和不完整性。
二、文法
文法用来描述语言的语法结构的形式规则。
举一个文法处理自然语言的例子,
He gave me a book.
这是一个句子,而一个句子的文法的规则如下:

所以经过下面的推导过程,就可以得到句子
He gave me a book。

三、语法描述的几个基本概念



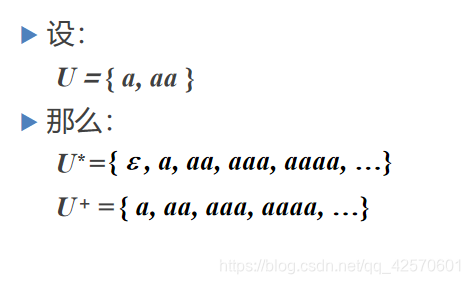
四、上下文无关文法
上下文无关文法G是一个四元组
G = (VT,VN,S,P)
,其中

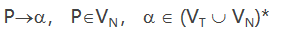
上面是上下文无关文法的产生式形式,上下文无关文法取名为“上下文无关”的原因就是因为字符P 总可以被字串 a(阿尔法) 自由替换,而无需考虑字符 P 出现的上下文。比如根据下面上下文文法规则,
<句子>
只要出现,就能被
<主语><谓语><间接宾语><直接宾语>
替换;
<主语>
只要出现,就可以被
<代词>
替换;而这些替换不需要考虑
句子
出现在什么地方,
主语
出现在什么地方,也就是不考虑文法的上下文。

举一个例子,定义只含
+
,
*
的算术表达式的文法
G=< {i,+,*,(,)},{E},E, P >
, 其中,P由下列产生式组成:
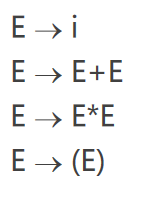
五、文法推导
推导过程
:对每一个句型(句型的接受在后面),该句型一定有一个推导过程(可能不唯一),推导过程一定对应一颗语法树(语法树也可能不唯一,语法树不唯一就说明文法具有二义性)。下面是推导的定义:

下面有
+
的读作
按非平方方式派生
,表示至少经过一步推导;有
*
读作
派生
,表示至少经过0步推导。

句型和句子
:只要是一个推导的右部,都可以称为句型;句子是一个特殊的句型,只含有终结符。

最左推导和最右推导
:
- 最左推导:每步推导中只改写最左边的那个非终结符
-
最右推导:每步推导中只改写最右边的那个非终结符,又称
规范推导

从一个句型到另一个句型的推导往往不唯一,如下面第一个是最左推导,第二个是最右推导:
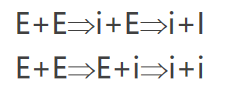
下面是一个文法的推导过程:
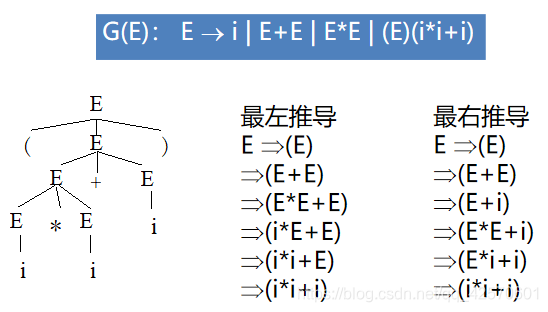
六、语法树与二义性(ambiguity)
文法二义性也就是,根据一个文法推导推导文法的某个句子时,会产生两个或以上个不同的语法树,就说这个文法具有二义性。

下面是根据文法G(E)推到出来的两个不同的语法树:
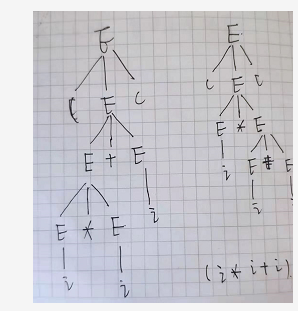
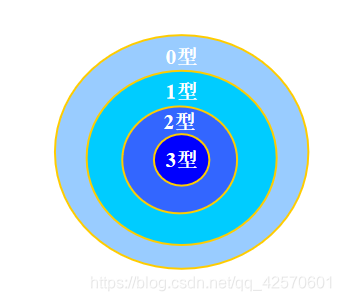
七、乔姆斯基形式语言体系
乔姆斯基于1956年建立形式语言体系,他把文法分成四种类型:0,1,2,3型
与上下文无关文法一样,它们都由四部分组成,但对产生式的限制有所不同。



四种文法能力强弱的比较: