104. 二叉树的最大深度
难度简单1442
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明:
叶子节点是指没有子节点的节点。
示例:
给定二叉树
[3,9,20,null,null,15,7]
,
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
思路:不断的往每个点的左右去找,并且分别记录左右的深度,返回大的那个就可以。
这个题目,对于每个点进行的都是
重复的操作
,并且,题目量也不大,所以递归是首选。
我本来是从二叉树的最小深度做的,都是看到这个题目,并且和下面的题目有难度的递进,所以就加进来了。
这个题目我AC
重点:
明白递归的结束条件:
1、空节点我们记录深度为0,所以return 0.
2、左右孩子都为空的节点就是结束的点,这里,我们记录深度为1 return 1.
3、分别用n,m记录左右节点的深度,并且返回较大的即可。
所以,代码如下:
int maxDepth(struct TreeNode* root){
if(!root) return 0;
else if(root->left==NULL&&root->right==NULL) return 1;
else{
int n=maxDepth(root->left);
int m=maxDepth(root->right);
if(n<m) return m+1;
return n+1;
}
}难度简单890
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:
叶子节点是指没有子节点的节点。
示例 1:
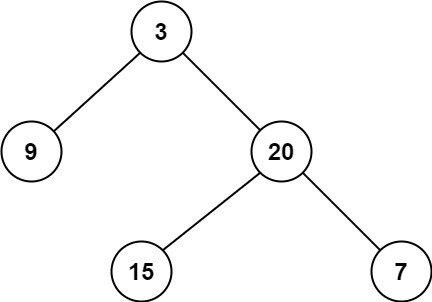
输入:root = [3,9,20,null,null,15,7] 输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6] 输出:5
提示:
-
树中节点数的范围在
[0, 105]
内 -
-1000 <= Node.val <= 1000
思路:不断向下寻找,并且每次向下都深度加1,直到找到一个左右孩子都是NULL的,结束查找,返回结果。
但是在这里有几个需要注意的点:
1、叶子节点是指没有子节点的节点。(我首先就在这里栽跟头了)
我首先的代码是:
int minDepth(struct TreeNode* root){
if(!root) return 0;
else if(root->left==NULL&&root->right==NULL) return 1;
else
{
int n=minDepth(root->left);
int m=minDepth(root->right);
if(n<m) return n+1;
else return m+1;
}
}
在这里,的通过率只有一半多一点,出错的地方就是在
叶子节点
这个地方,我在这里简单的把
距离根节点
最近的地方作为返回了。
2、明白递归结束的条件:
1.叶子节点的定义是左孩子和右孩子都为 null 时叫做叶子节点
2.当 root 节点左右孩子都为空时,返回 1
3.当 root 节点左右孩子有一个为空时,返回不为空的孩子节点的深度
4.当 root 节点左右孩子都不为空时,返回左右孩子较小深度的节点值
这里用图解的形式

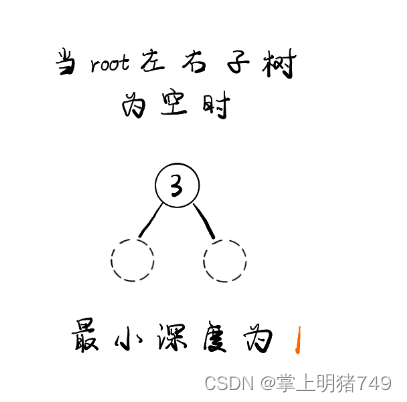
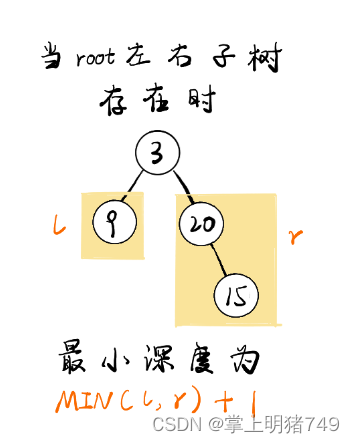
在这个图其实用2中情况:
如果左节点==NULL or 右节点==NULL 但是不管哪一个为NULL,对应的深度都是0,所以可以返回(左深度+右深度+1)
这样就很明确了怎么来确定结束条件
在最后返回的时候,我们只需要返回最小的那个深度+1就可以
一下代码就出来了
int minDepth(struct TreeNode* root){
if(!root) return 0;
if(root->left==NULL&&root->right==NULL) return 1;
int n=minDepth(root->left);
int m=minDepth(root->right);
if(root->left==NULL||root->right==NULL) return m+n+1;
return fmin(m,n)+1;
}——————————————————————————————————————————
难度简单1632
给定一个二叉树的根节点
root
,返回
它的
中序
遍历
。
示例 1:
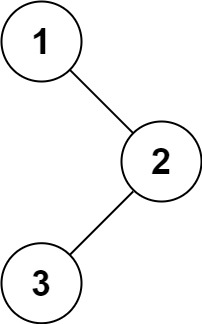
输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
思路:这个题目,我们对于每一个点都是一样的操作,都是先往左孩子,然后打印当前节点的值,然后往右孩子去。并且数据量不大,所以递归是首选。
在这里,我们的难点在什么呢:
还是什么时候结束递归,或者返回上一层。这里我们是对每一个不为空的节点操作的,所以,我们只需要在一开始限制在不为空的地方操作就可以。
这个不用多说,直接上代码:
void kk(struct TreeNode* root,int* res,int *returned)
{
if(root)
{
kk(root->left,res,returned);
res[(*returned)++]=root->val;
kk(root->right,res,returned);
}
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int *res=(int*)malloc(sizeof(int)*501);
*returnSize=0;
kk(root,res,returnSize);
return res;
}在力扣答题,对于简答题,唯一需要注意返回的方式。
在这里为什么写这个简单题目呢,其实是为了下面作铺垫的。
难度中等1528
给你二叉树的根节点
root
,返回其节点值的
层序遍历
。 (即逐层地,从左到右访问所有节点)。
示例 1:
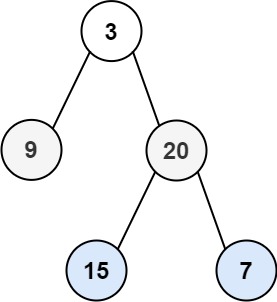
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
-
树中节点数目在范围
[0, 2000]
内 -
-1000 <= Node.val <= 1000
思路:这个题就是一层一层的往下找,那么怎么去做呢。其实在这里我个人推荐用队列的方式。我们先入队根节点,再保存根节点到返回的结果中去,再将根节点的左右子节点入队,并且出队队头。如此循环。
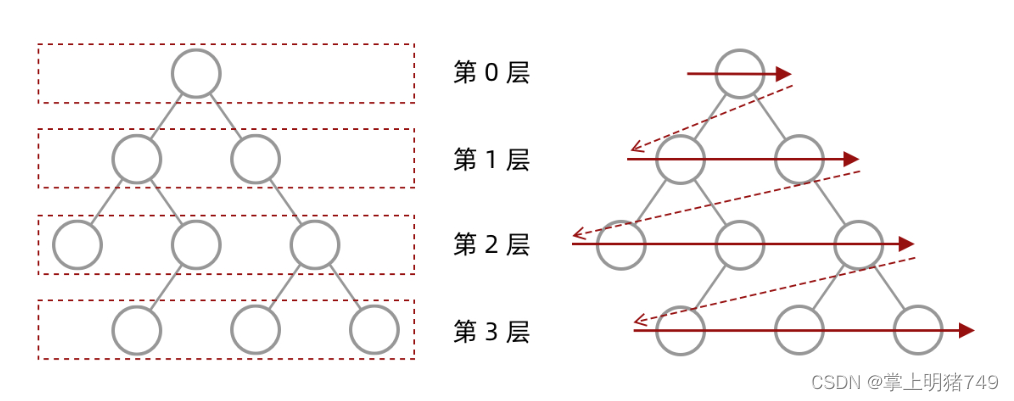
按这样的方式一层一层的输出。
我们举一个例子:
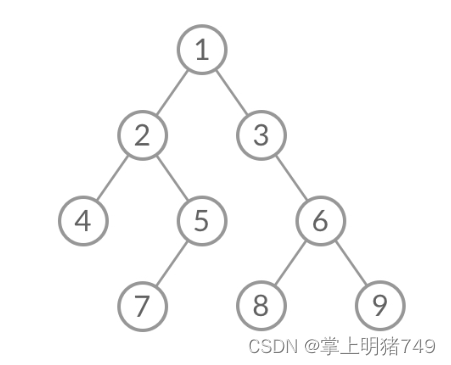
如图所示:我们先入队根节点(1),[1].
这个时候队列里面就只有1,然后我们将1的左右子节点入队,就是[1,2,3],再将队头出队[2,3].
我们再将队头的左右子节点入队[2,3,4,5],再出队队头[3,4,5],再入队队头的左右子节点[3,4,5,null,6].
如此循环。
结果就是
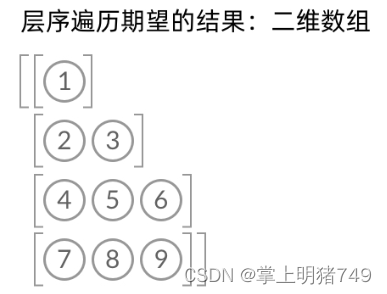
但是这样真的没有问题吗?
其实还是有一点小瑕疵的:
此处的瑕疵在2个点。
其中一个是某个点的左节点或者右节点为空,这个时候到底入不入队?
其次是,用c语言没有提供直接的队列,我们如何实现队列?
针对第一个问题,我个人建议是不入队。因为这样既方便操作,也节省空间。
第二个问题,这个队列,我不建议复写函数,其实没必要,这里,我个人建议用数组的方式去实现队列。
使用2个指针,头指针和尾指针。出队,队头指针++,入队,队尾指针++。
并且结束的条件,显而易见,那就是队头指针!=队尾指针
知道这些之后,我们附上代码:
#define MAX_SIZE 10000
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
*returnSize = 0;
if (root == NULL) {
return NULL;
}
struct TreeNode* queue[MAX_SIZE];
int ** res = (int**)malloc(sizeof(int*) * MAX_SIZE);
*returnColumnSizes = (int*)malloc(sizeof(int) * MAX_SIZE);
int head = 0, rear = 0;
queue[rear++] = root;
while (head != rear) {
int preRear = rear;
int k = 0;
res[*returnSize] = (int*)malloc(sizeof(int) * (preRear - head));
while (head < preRear) {
struct TreeNode* p = queue[head];
res[*returnSize][k++] = p->val;
if (p->left) {
queue[rear++] = p->left;
}
if (p->right) {
queue[rear++] = p->right;
}
head++;
}
(*returnColumnSizes)[*returnSize] = k;
(*returnSize)++;
}
return res;
}