数据分析学习记录(三)–主成分分析及在origin中的实现
注:本文仅作为自己的学习记录以备以后复习查阅
一 概念
主成分分析是一种数据分析的方法,尤其应用在
光谱降维领域
,降维是一种对高纬度特征数据的处理方法,对于存在相当大信息量的光谱数据来说,除了使用更直观的方式观察数据特征之外,降维是提升其数据处理速度和效率的一个十分有效的手段 。降维将高维数据保留下一些重要特征,去除噪声和不重要的特征,在一定的信息损失范围内,可以节约大量的时间和成本,因此
降维
也成为应用非常广泛的数据预处理方法。
数据降维有几大特点,
1)降维使得数据更易使用;2)降低算法开销;3)存在一定的信息损失
。用于光谱降维的算法最常用的包括主成分分析(PCA)、平行因子分析(PARAFAC)以及自动编码器(AE)。
二 PCA降维原理
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推,可以得到n个这样的坐标轴,也就是说我们通过只保留包含绝大部分方差的维度特征,将包含方差几乎为零的特征维度忽略以实现对特征数据的降维。
PCA的实现步骤如下:
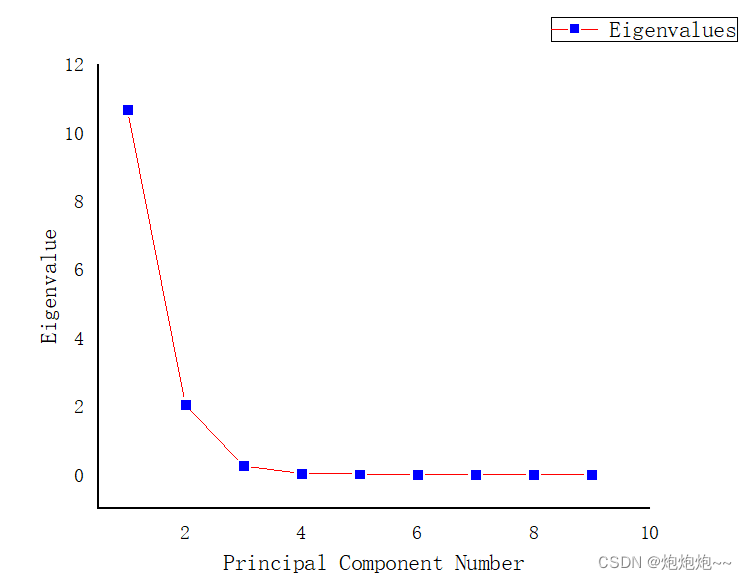
1)去除平均值,计算协方差矩阵;2)计算协方差矩阵的特征值和特征向量;3)将计算出来的特征值排序后保留前N个最大的特征值对应的特征向量;4)将原始特征转换到计算后得到的N个特征向量构建的新空间中
。
但PCA的
局限性
在于方法本质上来说是一个线性变换,但实际数据中大部分数据的形态都是非线性的,尤其是光谱数据,所以对于PCA这样的线性降维方法能操作的空间就非常小了。
三 使用origin实现PCA
这是一组由荧光区域积分法得出的五个区域的积分值,用这个数据给大家演示一下如何在origin中使用PCA。
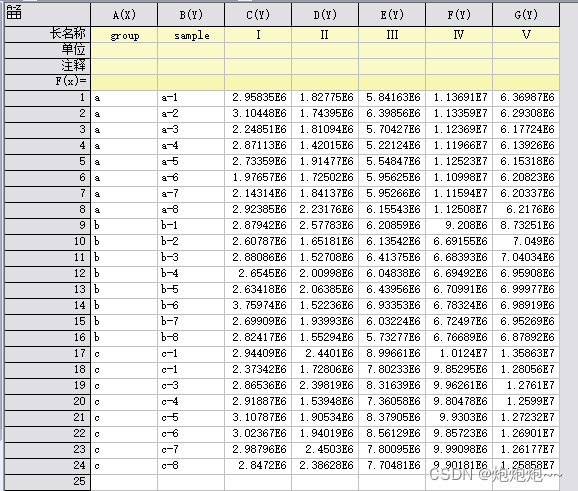
首先要确保你的origin中有pca这个插件,如果没有的可以去origin官网下载一个,然后将下载好的插件直接拖入app的区域origin就会自动添加。

把数据输入进origin中之后我们点击pca插件,会弹出一个提示窗,在提示窗中我们需要对应选择数据区域,inputdata这一个框中,我们需要填入所有数据,observation中选择样本列,group中我们就选择group列。
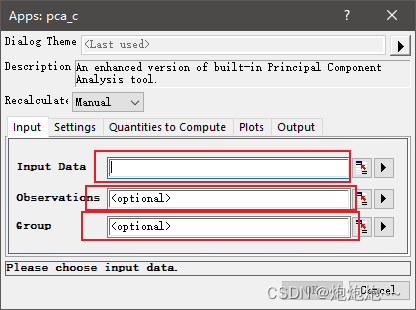
在plots这一选项卡中我们可以选择数据以2d还是3d的形式绘画以及选择是否生成置信度椭圆。
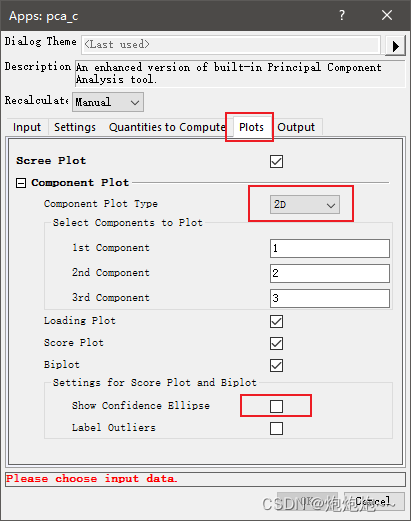
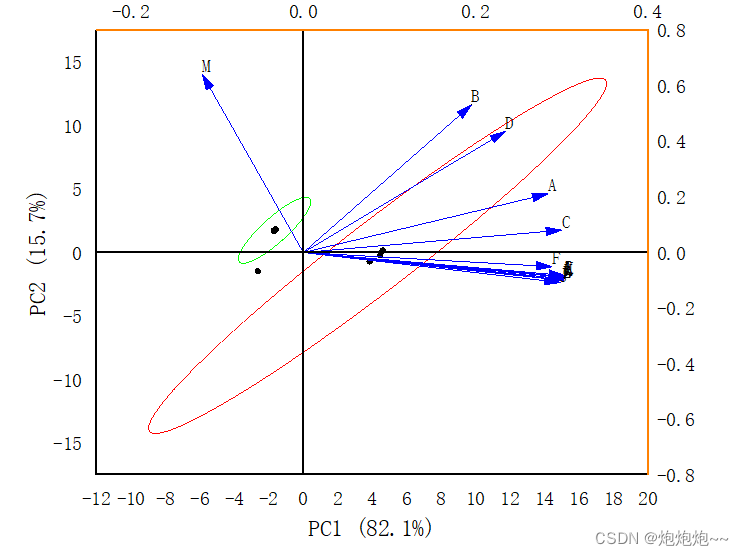
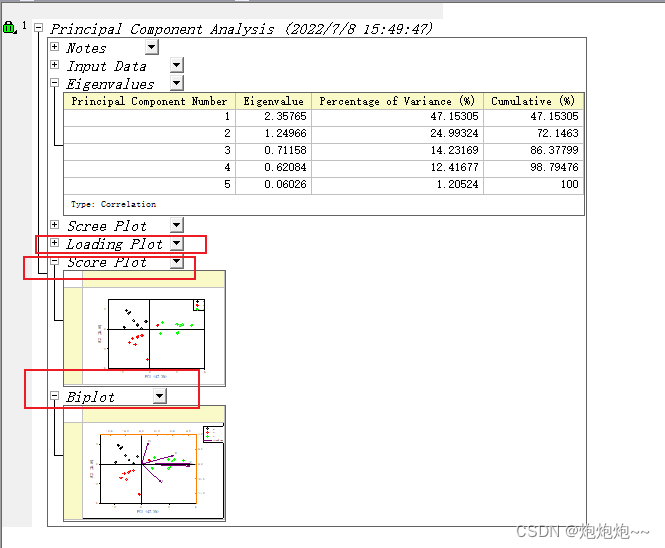
都选择好后我们就点击ok,随后origin会生成一系列的分析结果,包括载荷图、得分图和两者一起的 图,通过双击我们可以打开对应的图,然后对它进行一定的调整。
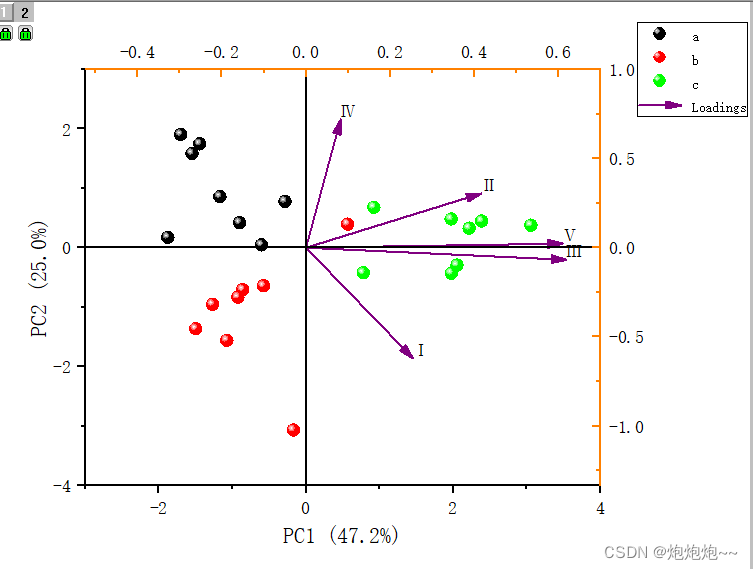
参考文献:
【1】林海明, 张文霖. 主成分分析与因子分析的异同和SPSS软件——兼与刘玉玫、卢纹岱等同志商榷[J]. 统计研究, 2005(03):65-69.
【2】Jian Y , David Z , Frangi A F , et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2004, 2004年26卷1期(1):131-7页.
【3】Ke Y . PCA-SIFT : A more distinctive representation for local image descriptors[J]. Proc. CVPR Int. Conf. on Computer Vision and Pattern Recognition, 2004, 2004.