博客

根据前文所述的模板方法，通过几道十分典型的例题来深入理解二分（单调

（sort）

的）模板：

1. 如何check();
2. 两个模板何时用；
3. stl的普及

本博客例题均出自洛谷与部分博主整理

目录

例一：查找编号

例二：A-B数对

例三：高考报名

例一：

查找编号

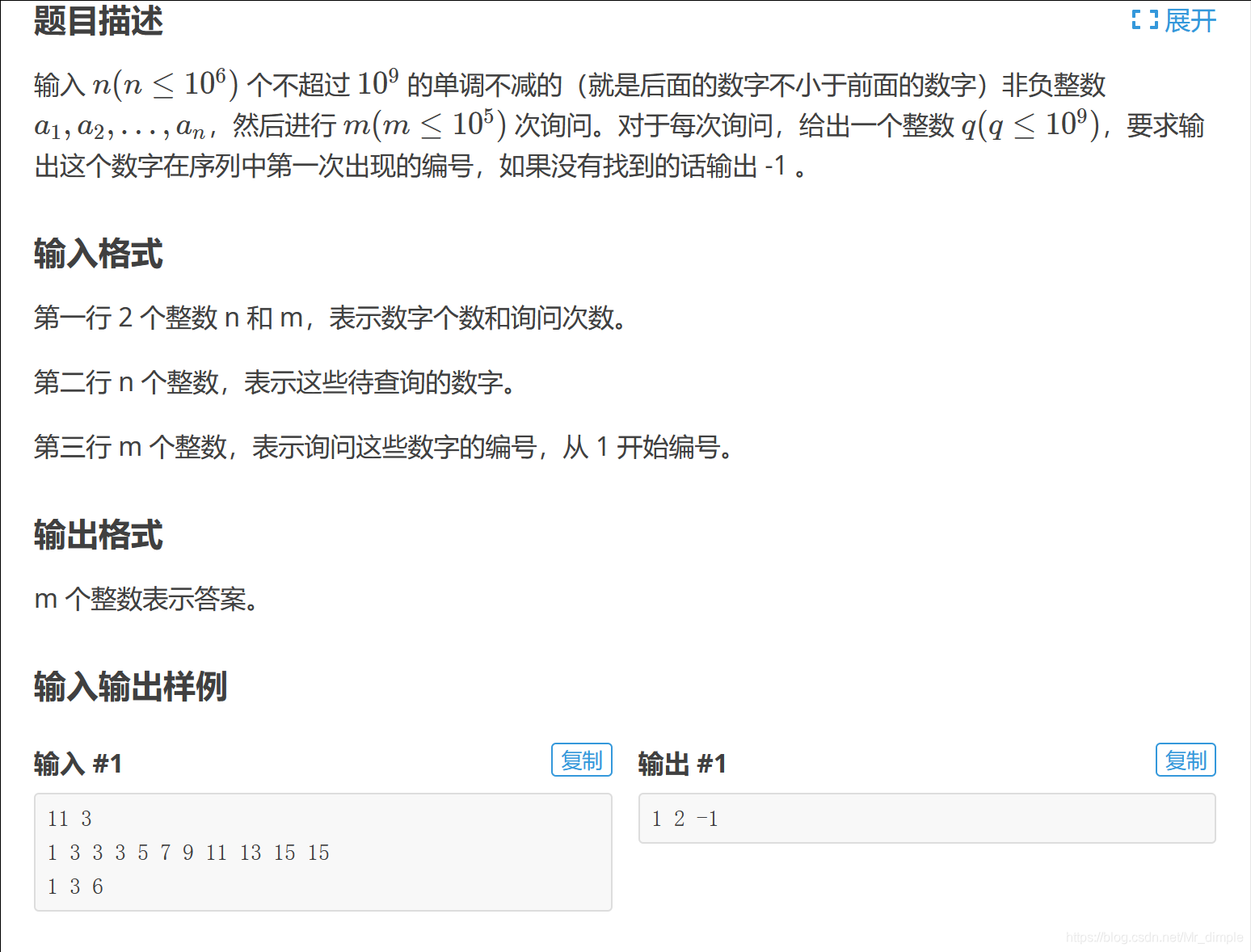
此题十分典型，要求查找最先出现的数字（也就是最左），那么运用模板一来解决

code：

#include<iostream>
using namespace std;

const int N=1000010;
int a[N],x,q,n;

int main(){
	cin>>n>>q;
	for(int i=1;i<=n;i++) cin>>a[i];
	
	while(q--)
	{
		cin>>x;
		int l=1,r=n; //左右边界 
		while(l<r) //因为是找第一次出现的位置，那就是尽量往左来，就用模板1 
		{
			int mid=l+r>>1;
			if(a[mid]>=x) r=mid; //判断条件，如果值大于等于目标值，说明在目标值右边，尽量往左来
			else l=mid+1;
		}
		if(a[l]!=x){ //如果找不到这个值 
			cout<<-1<<" ";
			continue;
		}
		cout<<l<<" ";
	}
	return 0;
} 

例二：

A-B数对

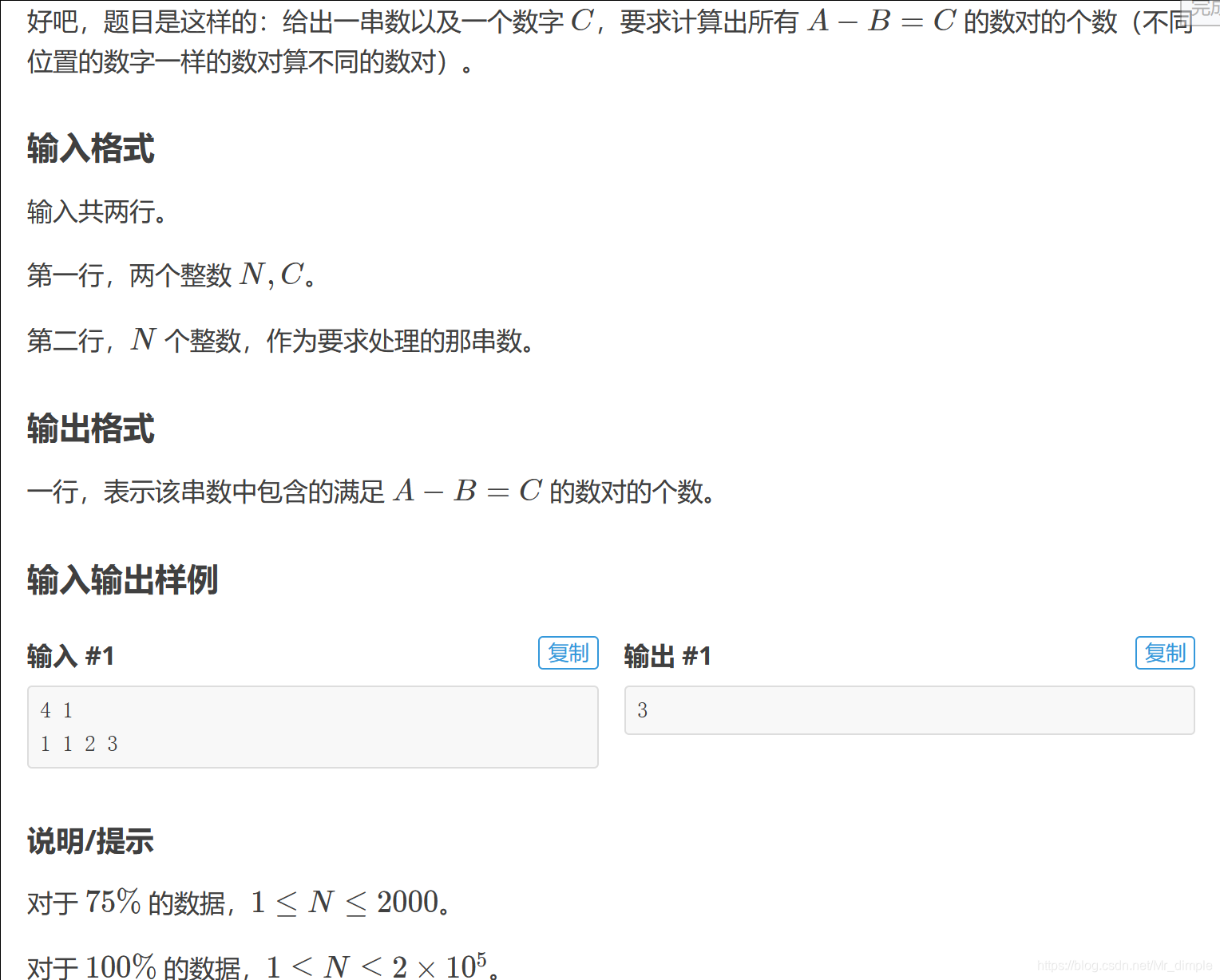
这道题就比较妙了，可以二分（利用二分，一遍循环枚举找B，中间二分找C，时间复杂度O(nlogn)）可以map（stl中自带的红黑树map，map映射）还有hash

code：

#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
int a[N];
int n, c;
long long cnt;
 
void bs(int x, int l, int r) {
	
	if (l >= r)return;
 
	while (l < r) {
		int mid = l + r >> 1;
		if (a[mid] >= x-c)r = mid;
		else l = mid + 1;
		
	}
	if (a[l] != x - c)return;
	else {
		int index = l;//获得最左边的下标
		cnt++;//已经确定a[l]=a[i]-C
		l = 0, r = n - 1;
		while (l < r) {
			int mid = l + r + 1 >> 1;
			if (a[mid] <= x - c)l = mid;
			else r = mid - 1;
			
		}
		if (a[l] != x - c) return;
		else cnt += l - index;//此时的l是最右边的下标
 
	}
 
}
int main(){
	
	cin >> n >> c;
 
	for (int i = 0; i < n; i++)scanf("%d", &a[i]);
 
 
	sort(a, a + n);	//排序
	//为每一个a[i]，查数组中所有的a[i]-C=B。
	for (int i = 0; i < n; i++) {
 
		bs(a[i],0,n-1);
	}
	cout << cnt;
	return 0;
}

1） upper_bound() ：在有序的

数组

连续地址 [begin,end) 中 找到第一个出现的位置，返回其地址。（>的位置）

2）lower_bound()：在有序的数组连续地址 [begin,end) 中 找到最后一个出现的位置，返回其地址。(>=的位置)

例如：upper_bound(a,a+n,a[i]+c) – a 的值就是第一个出现的下标。

#include<stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
long long a[200010],n,c,ans;
int main(){
	cin>>n>>c;
	for(int i=0;i<n;i++)
	    cin>>a[i];
	sort(a,a+n);
	for(int i = 0;i<n;i++)
	    ans += upper_bound(a,a+n,a[i]-c) - lower_bound(a,a+n,a[i]-c);

//视为A-C=B，当然也可以B+C=A,将for循环视为A，那么ans += upper_bound(a,a+n,a[i]+c) - lower_bound(a,a+n,a[i]+c);完全可以的！！！！！

	cout<<ans;
	return 0;
}

例三：

高考报名

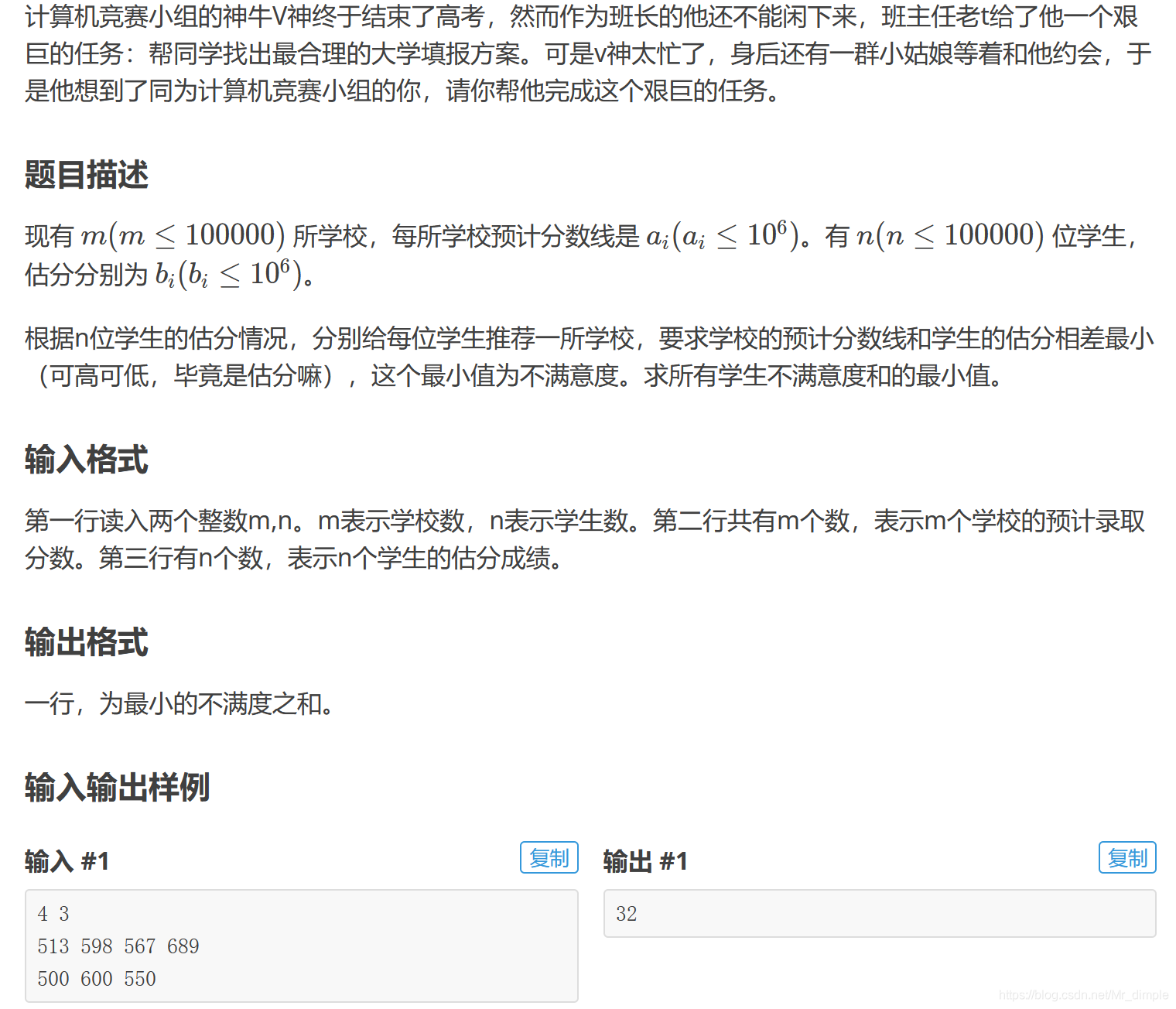
code：

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;
long long a[N],x,sum,n,m;

int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	sort(a+1,a+n+1); //排序勿忘 
	a[0]=-1e12;a[n+1]=1e12;	 //最后再解释
	
	while(m--)
	{
		cin>>x;
		int l=1,r=n+1;	//r设为n+1 
		while(l<r) //寻找第一个超过估分的学校，那它或它前面的一个学校就是目标学校 
		{
			int mid=l+r>>1;
			if(a[mid]>=x) r=mid;
			else l=mid+1;
		}
		if(a[l]-x<=x-a[l-1]) sum+=a[l]-x;
		else sum+=x-a[l-1];
	}
	
	cout<<sum;
	return 0;
	//a[0]=-1e12: 所有分数先可能都比估分大，那么l就为1，n-1就为0，故设a[0]为无穷小，则第一个值就为解 
	//a[n+1]=1e12: 所有分数线可能都比估分小，那么l就为n,a[l]-x可能为负，则设a[n+1]为无穷大，
				//并将r设为n+1，如此，l最大为n+1，则最后一个就为解 
}

stl方法：

while(m--)
	{
		cin>>x;
		int t=lower_bound(a+1,a+n+1,x)-a; //如果分数线都比估分低，那返回的位置是n+1，否则返回第一个大于等于估分的位置。
		if(a[t]-x<=x-a[t-1]) sum+=a[t]-x;
		else sum+=x-a[t-1];
	}