在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax),采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的2.56~4倍;
采样周期的整数倍不能检测到相位(状态)变化。每个信号可以展开成若干个正弦信号(甚至无穷多个),所以只需考虑一个正弦信号如何采样能完美重现。所以我的频率要大于他的二倍才行。频率带限的意义就是信号在时域的变化周期是有界限的,也就是说,信号在时域的波动存在一个最小周期。
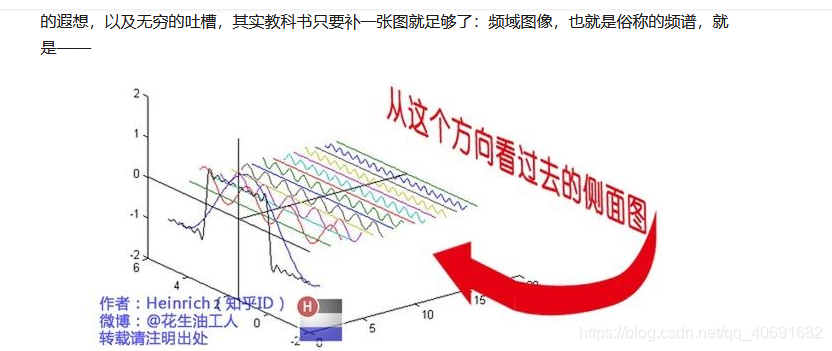
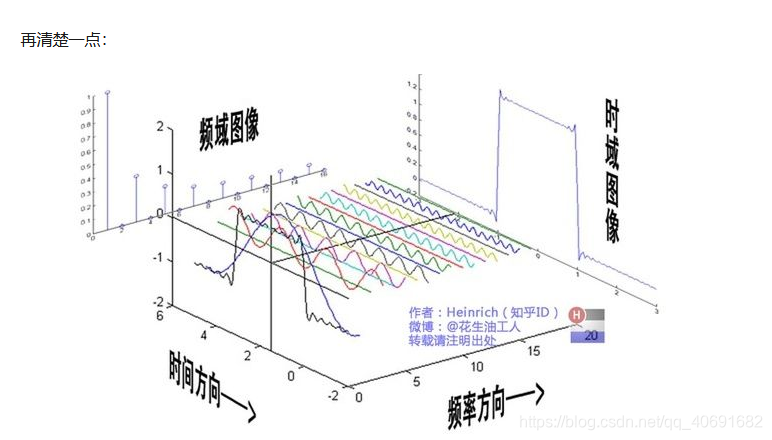
知道w与A就可以确定这个波形。


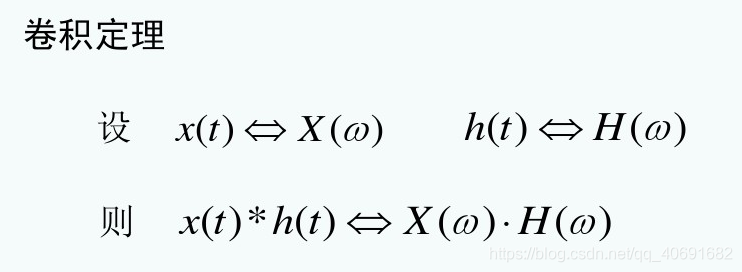
矩形函数的傅里叶变换是sa函数
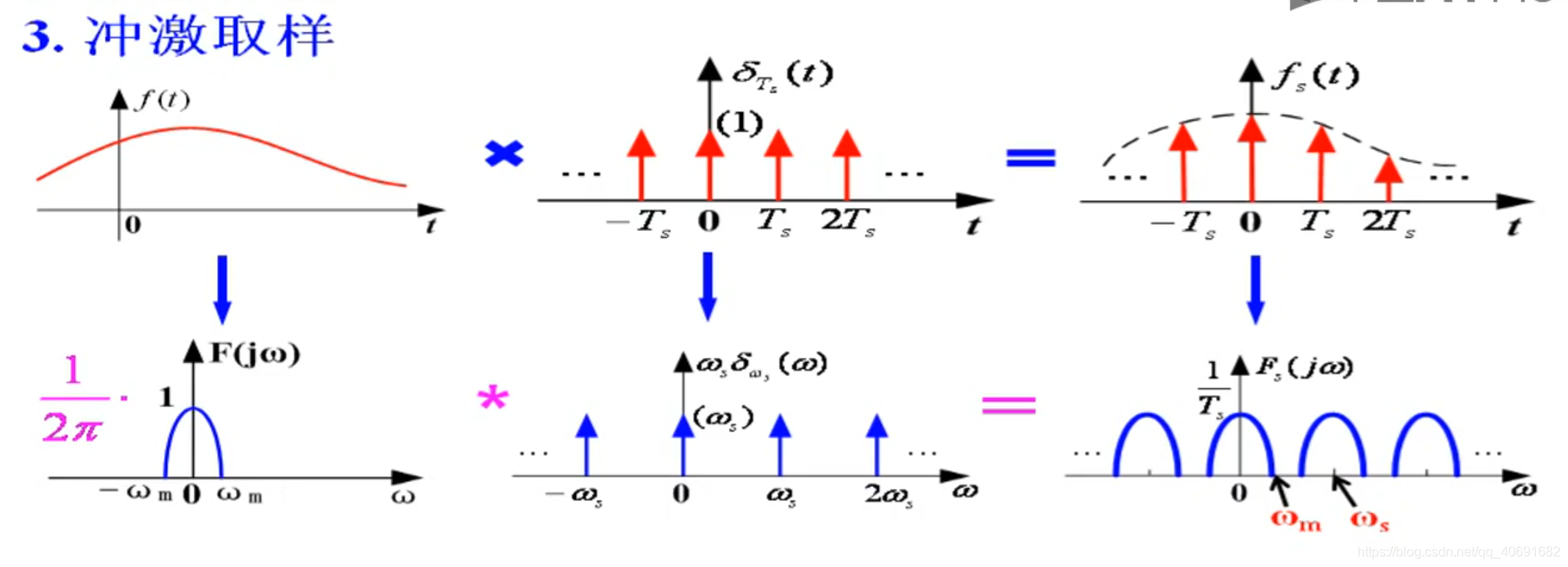
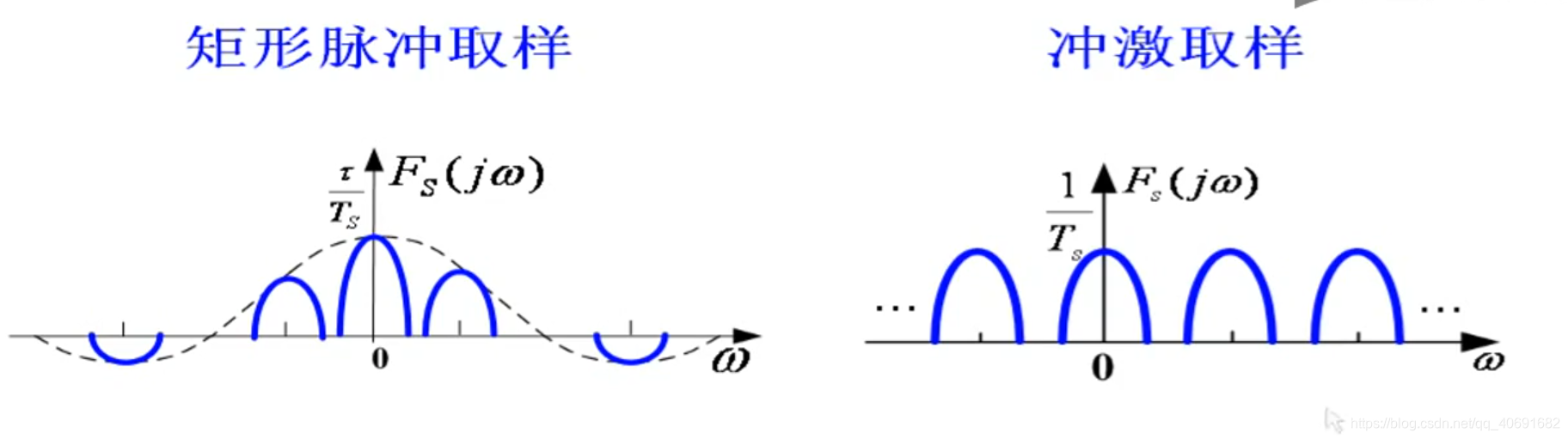
冲击取样是理想状态

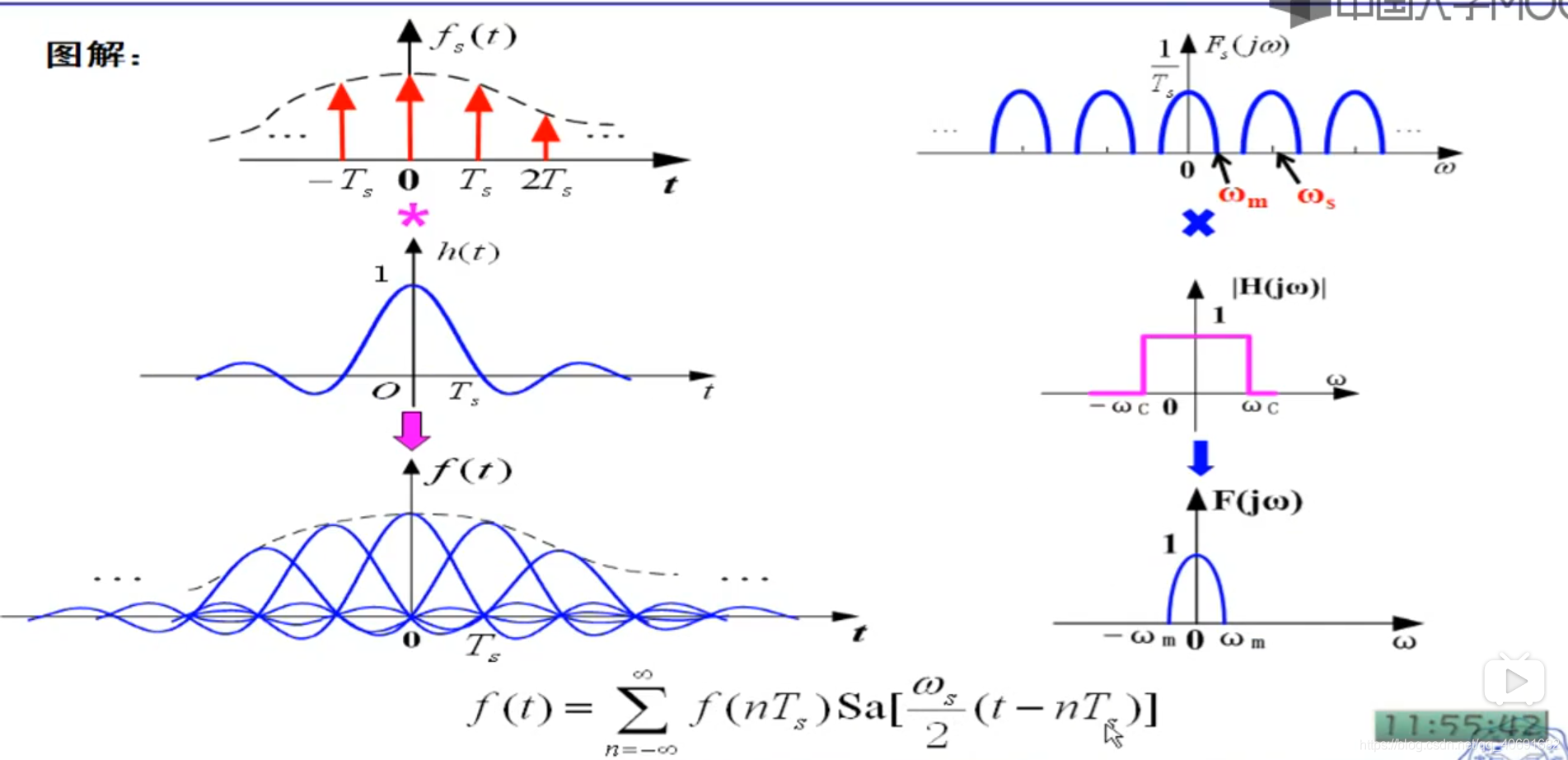
卷积sa是门函数目的是滤波出一个频谱。每次取一个叠加起来。时域抽样 相当于频域卷积
采样的实质是频谱的搬移于零中频低通信号而言,任何的信号都是有正负频谱的
时域和频域都是对信号的刻画
总结:时域f与冲击相乘 -》 频域卷积 -》频谱重复-》滤波出频谱(门函数)-》门函数的傅里叶变换为sa函数-》时域上sa相卷积-》累加
卷积的实质是信号的分解
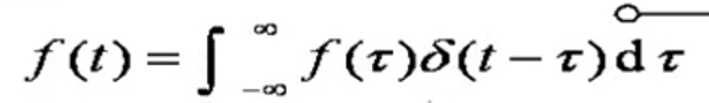

短时傅里叶变化:窗口大小固定,时间和频率是相矛盾的。本质是分时间段对信号做傅里叶变换,每个时间段内是这一段的频率信息,理论上波动快需要小窗。宽越小时间分辨率越高。本质是增加了时间参数。
连续小波变换:解决短时傅里叶变换窗口大小固定的问题,自适应窗口大小。有几种有代表性的小波函数。
信道带宽:所占用的频率宽度
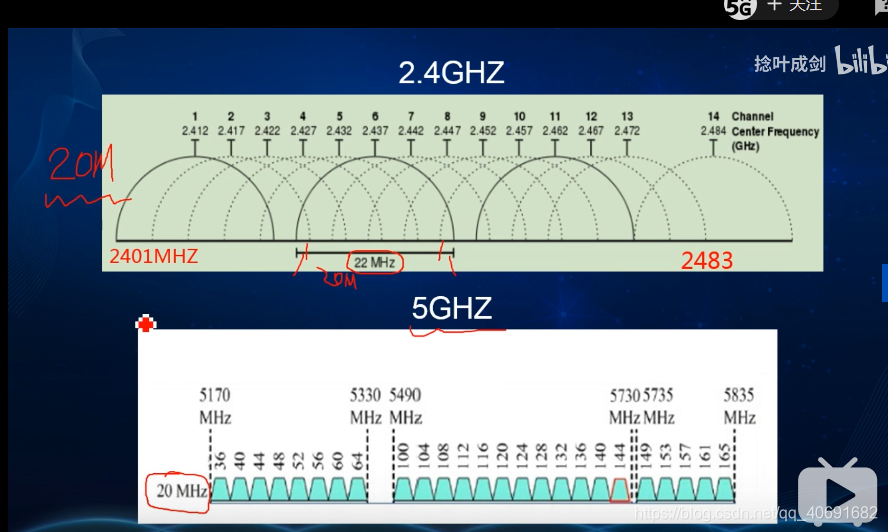
每次只能选其中一个使用也就是20M,2M剩余作为保护