1. 定义线加速度

和之前一样，速度是位置的微分



把得到的速度表达在另一个坐标系下面

这里，加速度是速度的微分



把得到的加速度表达在另一个坐标系下面



{c} frame 的原点对地的加速度就简化表达成 ac

2. 定义角加速度

线速度线加速度有这样的关系之外，角速度角加速度也有这样的对应关系，角速度的微分就是角加速度



简化表达，针对某个 frame {C}，它的旋转状态如果是对地的，就可以简化写为

3. 推导线加速度

由前面所学，知道A点对地的速度 = B点对地的速度 + 由B点看到A点的速度 + B所在坐标系在旋转过程中造成的向量 r(a对b) 的变化



对上边式子作微分



合并项之后，整理得

A点的加速度 = B点的加速度 + B相对于A看不到的部分，切向加速度（角加速度与r的叉积） + 法向加速度 + 人站在B坐标上看到的相对加速度 + 科式力

对应到机器人学中

4. 推导角加速度

{C} 对 {A} 的角速度 = {B} 对 {A} 的角速度 + {C} 对 {B} 的角速度（又因为在相加计算的过程中要转到同一个 frame 下，所以 {C} 对 {B} 的角速度前还要乘上一个旋转矩阵）

对这个式子作微分，这里 {C} 对 {B} 的部分有两个项，遵循前导乘后 + 前乘后导的原则，那对旋转矩阵求导是什么呢？

依照之前的想法，我们知道旋转矩阵是由三个单位向量所组成的，这三个单位向量互相正交，对旋转矩阵求导，相当于对三个单位向量求导，之前学过，对单位向量求导，它的长度不会变化，变化的只是它的方向。由于这里是旋转矩阵，所以单位向量的变化基本取决于整个坐标系旋转的状态，因此，

{B} 对 {A} 的旋转矩阵的倒数 = {B} 对 {A} 的角速度与旋转矩阵本身的叉积。（如红框部分所示）

5. 质量分布(Mass Distribution)

相对于 frame {A} 的惯性张量



惯性张量本身的特性：

• 是常实对称矩阵，在数学上是可正交对角化的
  
  

• 对角线元素之和为定值
  
  

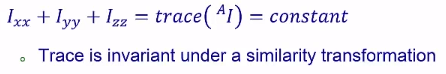
• 如果刚体的本身存在某个对称面，这个对阵面上下的值就会是零
  
  
  
  在算惯性矩阵的时候，必须要有转轴
  
  平行轴定理：
  
  
  
  

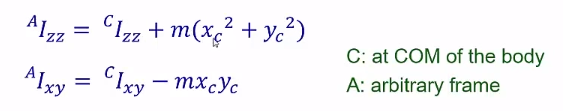
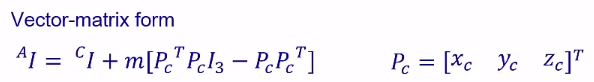
6. 牛顿-欧拉递推动力学方程

【大学物理知识回顾】


转动惯量 J

由刚体的各个质元相对于固定转轴的分布决定，与物体的运动以及所受的外力无关，是用于描述刚体相对于确定转轴特征的物理量。


动量 P=mv

，动量的变化量是合外力；


角动量L=Jw

，角动量的变化量是定轴转动刚体所受的力矩

下图所示是机械手臂中杆件的一节

杆件有加速度，必须受到惯性力F，杆件要转动，必须要受到扭矩N；

• 针对移动的部分，牛顿运动方程；
  
  线动量的变化量等于外力，牛顿第二运动定律；
• 针对转动的部分，欧拉方程；
  
  角动量的变化量等于力矩；
  
  

这里要特别小心

I

定义的 frame，因为在不同的 frame 下面，

I

的定义会不一样；和之前相反，我们不希望

I

定义在地坐标系下面，杆件在空间中是运动的，地坐标系不动，就等于说这个杆件以地坐标系来看的话，它和地坐标系之间的相对距离一直变动，所以它的

I

以地坐标来看的话就一直变动，这样取倒数的时候就需要考虑

I

的倒数，会使欧拉方程的求解变的复杂。

通常情况下我们会在质心的位置定义坐标系，由于这个坐标系与这个杆件固连，所以

I

不变



推导后的力矩由两项组成，第一项就是杆件的角加速度造成的，注意这里的

I

是对于建立在质心处的坐标系而言的，还有一部分就是由于系统的角速度造成的。

在 frame {i} 中表达连杆 i 的线加速度和角加速度，并且找到相邻连杆之间的线加速度以及角加速度关系。

6.1 外推法——计算速度和加速度

6.1.1 角加速度传递（旋转关节）

我们知道相邻两连杆间角速度关系如下，求导得：



坐标系转化

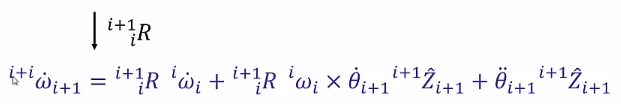
6.1.2 线加速度传递（旋转关节）

i+1 杆件的线加速度 = i 杆件的线加速度 + 切向加速度 + 法向加速度（还应该有两项科式力和相对的加速度，要是仔细看的话会发现，该式子是为了找到 {i+1}杆件 frame 的原点相对于 {i}杆件 frame 原点的加速度，而{i+1} 旋转时并不改变原点的位置，所以后边两项就没有了）



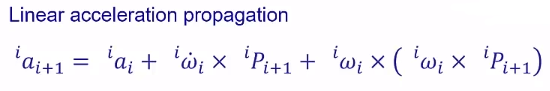
坐标系转化

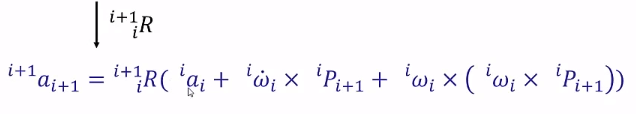
6.1.3 角加速度、线加速度传递（移动关节）

6.1.4 连杆质心的线加速度

除了上述的坐标原点的状态，连杆质心（COM）的状态也会用到，因为算惯性力的时候，就必须要算这个link 的COM的加速度是多少，我们才有办法借由这个加速度乘上质量m得到这个杆件受到的外力是多少（COM点在连杆的中部）

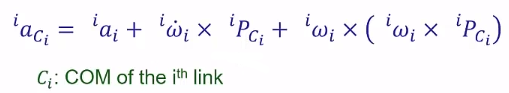
6.2 牛顿-欧拉方程

在找到了杆件和杆件之间加速度的关系后，现在要怎么跟力矩做一个连接？前面通过外推法计算出每个连杆质心的线加速度和角加速度后，运用牛顿-欧拉公式便可计算出作用在连杆质心上的惯性力和力矩：



假设 link(i) 有一个运动，那么基本上杆件所受的合力就等于运动的加速度乘上它的质量；

假设这个杆件有一个角加速度和角速度，假设也知道这个惯性张量对COM来看是已知的话，所受的外力矩就等于上述式子。

6.3 内推法——计算力和力矩

上面计算出每个连杆上的力和力矩后，我们就要计算出产生这些力和力矩的需要施加在关节上的关节力矩。

有了这个想法之后就可以分别来看力和力矩的状态。

以力的状态来说，力是由末端点往回算的（手臂末端点受到力，后面有力就代表前面关节都要承受住这个力，这个是和速度相反，速度是地的 link 不动，随着 link 往前增加，后面的 link 都要承载前面 link 的运动，然后再产生一个新的相对继续往后算）

将作用在连杆i ii上所有的力相加，得到力平衡方程：


frame {i} 所需要的力 = {i+1} 这个 frame 的力 + 让 {i} 本身产生运动所需要的惯性力

将所有作用在质心上的力矩相加，得到力矩平衡方程：

力矩是建立在相似的概念上的，力矩这里会有点复杂，在于杆件原本受到的力也会产生力矩，所以力矩所包含的项就会比较多。


i 杆件所要承受的力矩 = i+1 所要承受的力矩（i+1之后的杆件传到 i+1 的力矩） + 让 i 产生转动所需的惯性力矩 + 惯性力 Fi 所产生的力矩 + i+1 杆件的外力所产生的力矩

那么怎么求得关节力矩呢？

在静力学中，可以通过计算一个连杆施加于相邻连杆的力矩在Z方向上分量求得：

关节类型不同，计算马达负载的方式也会不同。针对旋转关节，会用力矩对 Z 轴做投影；针对移动关节，用力对 Z 轴做投影。让我们真正算出来在真正在动力学考量下面，我们的系统在完成运动时所需要的各个 joint 的力矩是什么。

7. 补充说明

针对这个，有几个其他的想法要补：

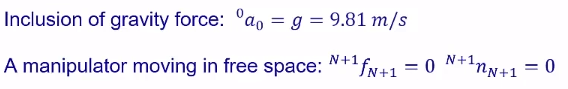
• 包含重力场（在考虑的时候加上与重力场加速度g等大反向的加速度就可以抵消重力那部分的作用了，就不会不小心忽略掉重力场的作用）
• 假设手臂在空中晃来晃去，手臂末端没有夹持东西或者做一些操作，那最后一个 joint 本身的力和力矩就可以设定为零，再借由这个为零的条件往回算。
  
  

我们现在有了运动的状态，有了速度和加速度的公式，也有了力和力矩的公式，那也就是真正面对一个问题的时候，先把运动状态算完，运动状态是由地杆往上算，算到末端执行器之后，就可以获取整个手臂的速度和加速度状态。

有了这个之后再导入所谓的力，假设末端点会有某个力，再往回算，获取力和力矩。

上行是计算速度和加速度，下行是计算力和力矩，都计算完之后，我们才能由力和力矩去投影计算 每一个joint 所需要的出的力是多少。

注意：

• 旋转关节和移动关节用的公式是不一样的，所以在推导的过程中要选对公式；
• 这是一个通用的架构，可以应用于任意的手臂；
• 适用于计算机迭代计算。

【资料分享】


中正平和的机器人学笔记——5. 机械臂动力学