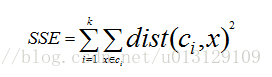K-Means聚类算法的研究与改进
*
摘 要:K-Means算法是基于划分的聚类算法中的一个典型算法,该算法有操作简单、采用误差平方和准则函数、对大数据集的处理上有较高的伸缩性和可压缩性的优点.但是该算法还存在着一些随机初始聚类中心导致算法不稳定的缺陷,本文研究了传统K-Means的算法的思想、原理及优缺点,并针对其对初始值依赖的缺陷,提出并研究了一种改进算法K-Means++,该算法对选取初始聚类中心的方法进行了改进.经过实验证明,K-Means++算法有效的提高了算法效率和稳定性,减少了算法开销.
关键词:聚类算法,K-Means算法,数据挖掘
Research and Improvement of K-Means Clustering Algorithm
Abstract:
K-Means algorithm is a typical algorithm based on partitioned clustering algorithm. It has the advantages of simple operation, error squared sum criteria function, high scalability and compressibility for processing large data sets advantage. However, there are still some shortcomings in this algorithm, such as stochastic initial clustering center, which results in instability of the algorithm. This paper studies the concept, principle, advantages and disadvantages of the traditional K-Means algorithm and proposes and studies the defects of the original K- An improved algorithm K-Means ++, which improves the method of selecting initial cluster centers. Experimental results show that the K-Means ++ algorithm effectively improves the efficiency and stability of the algorithm and reduces the cost of the algorithm.
Key words:
clustering algorithm, K-Means algorithm, data mining
K-Means聚类算法是最为经典,同时也是使用最为广泛的一种基于划分的聚类算法,它属于基于距离的聚类算法.所谓基于距离的聚类算法是指采用距离作为相似性度量的评价指标,也就是说两个对象之间距离越近,则它们的相似性越大.这类算法的目标通常是将距离比较相近的对象组成簇,从而得到紧凑而独立的不同簇,因此将这种算法称为基于距离的聚类算法.K-Means聚类算法就是其中比较经典的一种算法,作为数据挖掘的重要分支,K-Means聚类算法具有算法简单、易于实现、易于扩展,并且能够处理大数据集的优点,但K-Means也有一些不可避免的缺点,比如对初值的比较敏感,不同的初始聚类中心会导致不同的聚类结果,使得算法不稳定,容易陷入局部最优的情况.本文针对K-Means算法的这个缺点提出一种改进算法,实验证明改进算法能够有效提高算法效率和稳定性,并且减少损失.
本文第一节介绍了传统K-Means算法的原理、算法步骤及优缺点;第二节针对传统K-Means算法随机选取初始聚类中心的做法会导致算法的不稳定性的缺点提出了改进算法K-Means++,其主要思想是在选取初始中心聚类的时候遵循初始的聚类中心之间的距离应尽可能远的原则;第三节实现了K-Means和K-Means++算法,并将两个算法做了比较,实验证明K-Means++算法有效提高了算法的效率和稳定性,最后对本文进行了总结.
1 传统K-Means算法
1.1 K-Means算法原理
K-means算法采用迭代更新的思想,该算法的目标是根据输入的参数k(k表示需要将数据对象聚成几簇),其基本思想为:首先指定需要划分的簇的个数k值,随机地选择k个初始数据对象作为初始聚类或簇的中心;然后计算其余的各个数据对象到这k个初始聚类中心的距离,并把数据对象划分到距离它最近的那个中心所在的簇类中;然后重新计算每个簇的中心作为下一次迭代的聚类中心.不断重复这个过程,直到各聚类中心不再变化时或者迭代达到规定的最大迭代次数时终止.迭代使得选取的聚类中心越来越接近真实的簇中心,所以聚类效果越来越好,最后把所有对象划分为k个簇.
1.2 K-Means算法步骤
K-Means算法步骤如下:
1.3 K-Means算法优缺点
K-means算法是解决聚类问题的经典算法,这种算法简单快速.当结构集是密集的,簇与簇之间区别明显时,聚类的结果比较好.在处理大量数据时,该算法具有较高的可伸缩性和高效性,它的时间复杂度为O (nkt),n是样本对象的个数,k是分类数目,t是算法的迭代次数.一般情况下,k<<n,t<<n.
但是,目前传统的K-means算法也存在着许多缺点,有待于进一步优化.
(1) K-Means聚类算法需要用户事先指定聚类的个数k值.在很多时候,在对数据集进行聚类的时候,用户起初并不清楚数据集应该分为多少类合适,对k值难以估计.
(2) 对初始聚类中心敏感,选择不同的聚类中心会产生不同的聚类结果和不同的准确率.随机选取初始聚类中心的做法会导致算法的不稳定性,有可能陷入局部最优的情况.
(3) 对噪声和孤立点数据敏感,K-Means算法将簇的质心看成聚类中心加入到下一轮计算当中,因此少量的该类数据都能够对平均值产生极大影响,导致结果的不稳定甚至错误.
(4) 无法发现任意簇,一般只能发现球状簇.因为K-Means算法主要采用欧式距离函数度量数据对象之间的相似度,并且采用误差平方和作为准则函数,通常只能发现数据对象分布较均匀的球状簇.
本文主要针对K-Means算法的第二个问题即初始值对聚类结果的影响进行分析和研究,考虑改进初始聚类中心的选择,从而减少K-Means算法对初始值的依赖性,提高算法效率.
2 改进算法K-Means++
2.1 K-Means++算法原理
传统的K-means算法对初始聚类中心敏感,聚类结果随不同的初始聚类中心而波动.针对K-means聚类算法中随机选取初始聚类中心的缺陷,提出了一种新的基于数据分布选取初始聚类中心的K-Means++算法.
K-Means++算法在整体思想上与K-Means算法相差不大,同样是采取迭代更新的思想.其主要改进在第一步选取k个初始聚类中心时,不再是在整个数据集中随机选取k个数据对象作为初始聚类中心,而是遵循初始的聚类中心之间的距离应尽可能远的原则选取k个初始聚类中心.K-Means++算法选取初始聚类中心的主要思想为
:
假设已经选取了n个初始聚类中心(0<n<
k
)
,
则在选取第n+1个聚类中心时
:
距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心
.
在选取第一个聚类中心(n=1)时同样通过随机的方法
.
2.2 K-Means++算法步骤
K-Means++算法步骤如下:
综上所述即为K-Means++算法的完整步骤.
3 改进算法K-Means++与K-Means算法的比较
3.1 数据集
我们使用了一个简单的包含300个样本,每个样本具有两个属性的二维数据集,将其可视化如下图1所示,可以看到数据集大概分为3簇,因此我们将k值确定为3,在此基础上实现K-Means算法和该改进后的K-Means++算法.
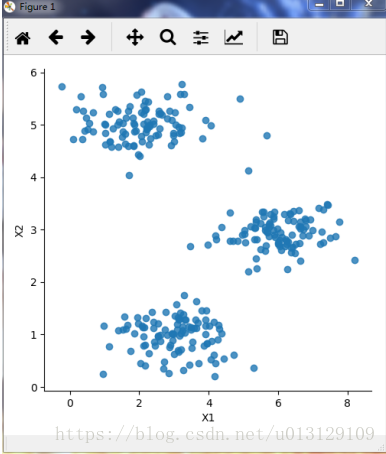
图1 数据集
3.2 评估标准
上文提到K-Means算法采用误差平方和准则函数,算法目标则是最优化该误差平方和准则函数,并且本文中实现算法时使用的停止条件为达到最大迭代次数.因此,我们使用误差平方和(SSE)作为算法的评估标准.
(1)
其中dist表示每个点到它所属的簇的中心点的距离,SSE值即为所有样本点到它所属的簇的中心点的距离的平方和.在相同迭代次数的条件下,SSE值越小,则说明算法越好,损失越小.
3.3 算法比较
在数据集上分别使用K-Means算法和K-Means++算法,迭代次数与算法的SSE值的关系如下表1所示(保留小数点后两位).
Table 1
.Comparison of two algorithms SSE value
表1 两种算法SSE值比较
|
迭代次数 |
K-Means算法SSE值 |
K-Means++算法SSE值 |
|
2 |
872.47 |
266.82 |
|
3 |
851.15 |
266.66 |
|
4 |
690.14 |
266.66 |
|
6 |
276.68 |
266.66 |
|
8 |
266.66 |
266.66 |
|
10 |
266.66 |
266.66 |
根据上表可以看出,传统K-Means算法在第8次迭代时收敛至全局最小值,此时的SSE值为266.66,而K-Means++算法在第3次迭代时就已经收敛至全局最小值,此时的SSE值也为266.66.因此可以证明改进后的K-Means++算法效率大大提升,能够在开销更小的情况下,快速而稳定的收敛至全局最小值,达到较好的聚类效果.
迭代次数为4时,将两种算法的聚类结果可视化如下图2、图3所示.由两张结果图对比可以看出,K-Means++算法的聚类效果比K-Means算法更好,能够更清楚的将原始数据点按照距离相似性的远近分成了3簇,其中红色X标记为最后一次分类的样本中心点.
另外,经过实验证明,迭代次数足够大并且实验次数足够多时,K-Means算法和K-Means++算法都能够收敛至全局最小值,最终也都能达到较好的聚类效果.但是K-Means算法选取初始聚类中心的随机导致了K-Means算法的不稳定性,在改进了选取初始聚类中心的方法以后,K-Means++算法能够更快的收敛,算法效果更好.
综上,可以得到结论,改进后的K-Means++算法在一定程度上降低了传统K-Means算法对初始值的依赖,降低了算法的不稳定性,有效提高了算法效率,减少了算法开销.
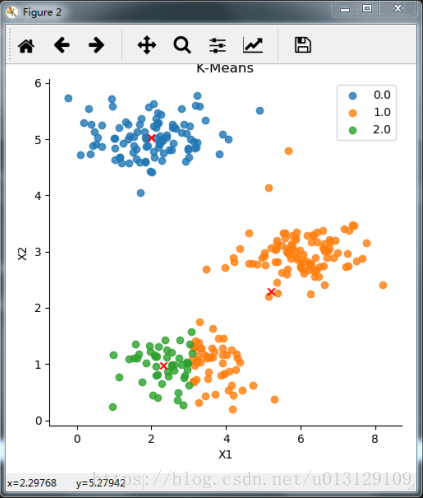
图2 K-Means聚类效果(迭代次数4)
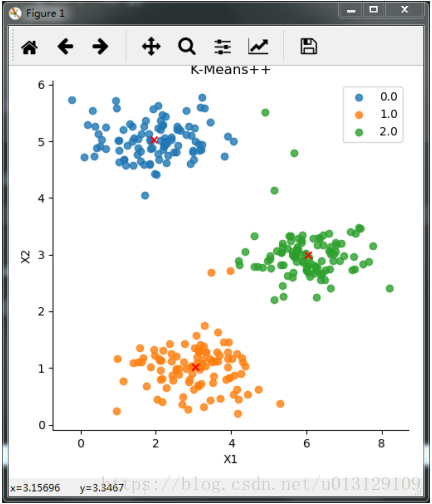
图3 K-Means++ 聚类效果(迭代次数4)
4 小结
K-Means聚类算法作为基于划分聚类算法的一个典型算法,在数据挖掘中被广泛应用,经常被用来作为预处理步骤.本文重点研究了K-Means算法的思想、原理及其优缺点,并针对传统K-Means算法随机选取初始聚类中心导致算法不稳定的缺点提出了改进算法K-Means++,K-Means++算法是基于数据分布选取初始聚类中心的改进算法,其主要思想是初始的聚类中心之间的距离应尽可能远的思想.本文也重点研究了K-Means++算法的思想与原理,其改进可以有效避免随机选取初始聚类中心的盲目性,实验证明改进后的K-Means++算法在稳定性和速度上都比传统K-Means算法有了较大的提升.
References
:
[1]
王莉. 数据挖掘中聚类方法的研究[D].天津大学,2004.
[2]
常彤.K-means算法及其改进研究现状[J].通讯世界,2017(19):289-290.
[3]
陈伟,李红,王维.一种基于Python的K-means聚类算法分析[J].数字技术与应用,2017(10):118-119.
[4]
张琳,陈燕,汲业,张金松.一种基于密度的K-means算法研究[J].计算机应用研究,2011,28(11):4071-4073+4085.
[5]
李卫平.对k-means聚类算法的改进研究[J].中国西部科技,2010,9(24):49-50.
[6]
夏长辉.一种改进的K-means聚类算法[J].信息与电脑(理论版),2017(14):40-42.
[7]
孙佳,胡明,赵佳.K-means初始聚类中心选取优化算法[J].长春工业大学学报,2016,37(01):25-29.
[8] David Arthur,Sergei Vassilvitskii. k-means++: The Advantages of Careful Seeding.
symposium on discrete algorithms
.
2007.http://ilpubs.stanford.edu:8090/778/1/2006-13.pdf