博客

题目描述

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

思路：

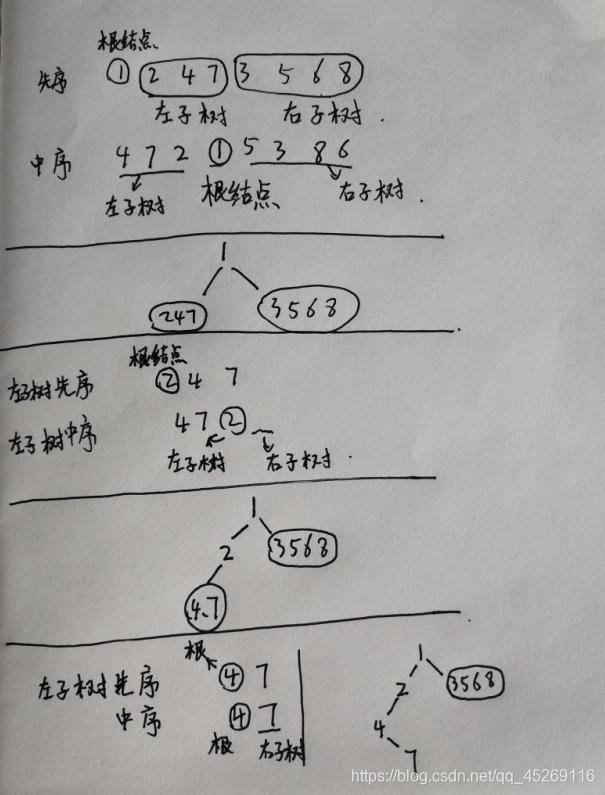
先序遍历结果： 1 2 4 7 3 5 6 8

中序遍历结果： 4 7 2 1 5 3 8 6

1、先序遍历的第一个数据就是根节点

2、中序遍历根节点左边的就是左子树，右边的就是右子树



3、根据第1、2步可得到根节点、左子树、右子树，接下来就是把左子树、右子树进行相同的操作

代码：

#include<iostream>
#include<vector>
using namespace std;

//Definition for binary tree 
struct TreeNode {
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};


TreeNode* reConstructBinaryTree(vector<int> &pre, vector<int> &vin) 
{
    //节点为空
    if (pre.empty())
        return NULL;

    int size = pre.size();
    //把根节点放到树里，注意，结构体的构造函数必须带一个值
    TreeNode* tree = new TreeNode(pre[0]);
    //只有一个节点
    if (size == 1)
    {
        return tree;
    }

    //找到中序遍历的根节点的下标：

    int inRoot = 0;
    for (; inRoot < size; ++inRoot)
        if (pre[0] == vin[inRoot])
            break;

    //把子树放到的相应数组里
    vector<int> preLeft, preRight, vinLeft, vinRight;
    for (int i = 1; i <= inRoot; ++i)
        preLeft.push_back(pre[i]);

    for (int i = inRoot + 1; i < size; ++i)
        preRight.push_back(pre[i]);

    for (int i = 0; i < inRoot; ++i)
        vinLeft.push_back(vin[i]);

    for (int i = inRoot + 1; i < size; ++i)
        vinRight.push_back(vin[i]);

    tree->left = reConstructBinaryTree(preLeft, vinLeft);
    tree->right = reConstructBinaryTree(preRight, vinRight);
    return tree;

}

//遍历顺序：根左右
void PreOrder(TreeNode* everyTreeNode)
{
	if (everyTreeNode)
	{
		cout << everyTreeNode->val << " ";
		PreOrder(everyTreeNode->left);
		PreOrder(everyTreeNode->right);
	}
}
//遍历顺序：左根右
void InOder(TreeNode* everyTreeNode)
{
	if (everyTreeNode)
	{

		InOder(everyTreeNode->left);
		cout << everyTreeNode->val << " ";
		InOder(everyTreeNode->right);
	}
}

int main()
{
	vector<int> pre = { 1, 2, 4, 7, 3, 5, 6, 8 };
	vector<int> vin = { 4,7,2,1,5,3,8,6 };

	TreeNode* tree = reConstructBinaryTree(pre, vin);
	
    cout << endl;
    cout << "先序遍历： " << endl;
	PreOrder(tree);
    cout << endl;
    cout << "中序遍历： " << endl;
    InOder(tree);

	return 0;
}

小结：

当然，我的代码可改进的地方还很多，比如不穿先序中序数组，而是传原始数组和左右子树的开始结束下标，这样就不必开辟新的空间存储子树数组的数据了。

大佬的代码：

public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        TreeNode root=reConstructBinaryTree(pre,0,pre.length-1,in,0,in.length-1);
        return root;
    }
    //前序遍历{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}
    private TreeNode reConstructBinaryTree(int [] pre,int startPre,int endPre,int [] in,int startIn,int endIn) {
         
        if(startPre>endPre||startIn>endIn)
            return null;
        TreeNode root=new TreeNode(pre[startPre]);
         
        for(int i=startIn;i<=endIn;i++)
            if(in[i]==pre[startPre]){
                root.left=reConstructBinaryTree(pre,startPre+1,startPre+i-startIn,in,startIn,i-1);
                root.right=reConstructBinaryTree(pre,i-startIn+startPre+1,endPre,in,i+1,endIn);
                      break;
            }
                 
        return root;
    }
}