8.20 N 叉树的前序遍历【589】
8.20.1 题目描述
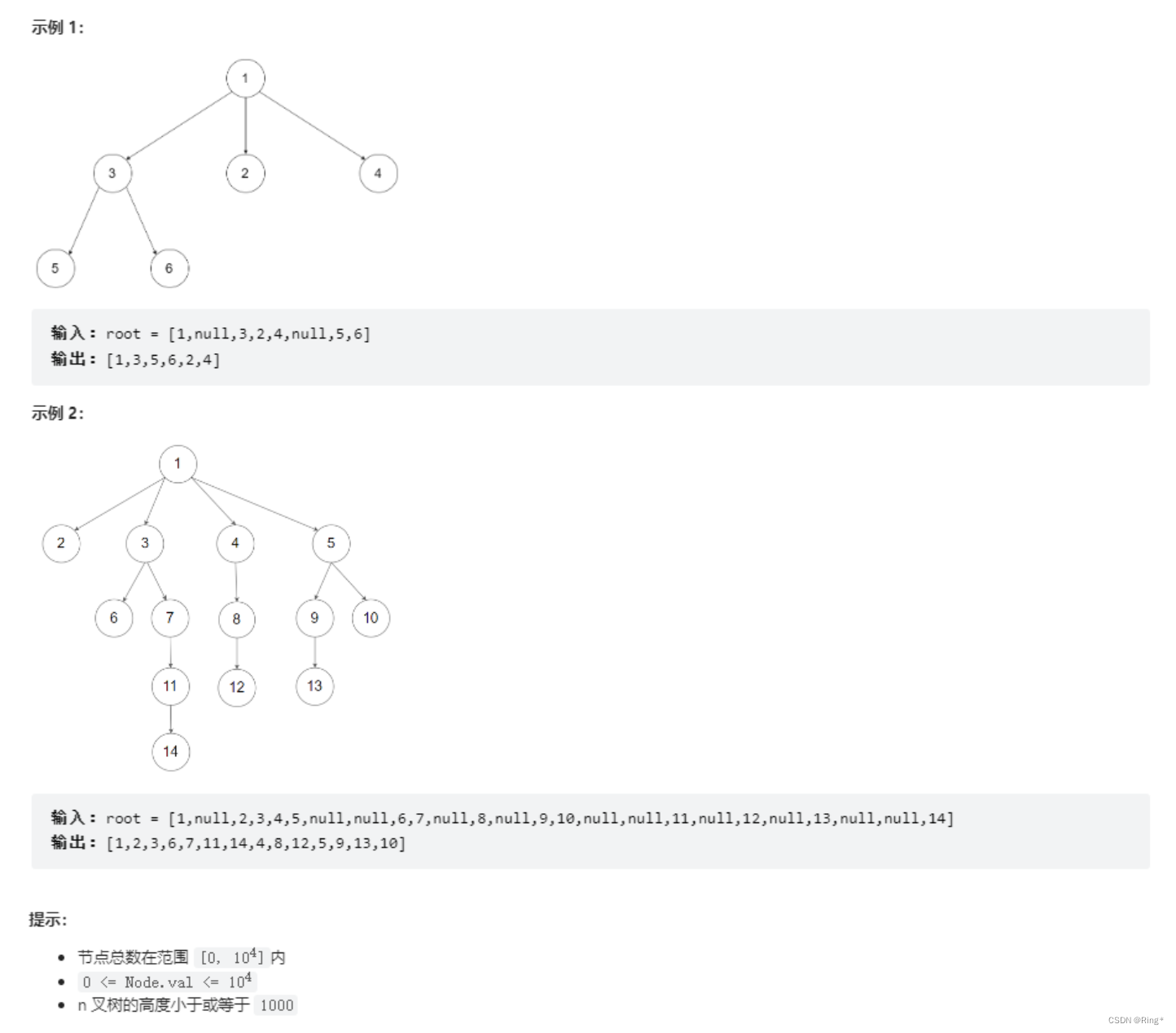
给定一个 n 叉树的根节点 root ,返回 其节点值的 前序遍历 。
n 叉树 在输入中按层序遍历进行序列化表示,每组子节点由空值 null 分隔(请参见示例)。
8.10.2 方法一:递归
思路
递归思路比较简单,N 叉树的前序遍历与二叉树的前序遍历的思路和方法基本一致,可以参考「144. 二叉树的前序遍历」的方法,每次递归时,先访问根节点,然后依次递归访问每个孩子节点即可。
代码
class Solution {
public List<Integer> preorder(Node root) {
List<Integer> res = new ArrayList<>();
helper(root, res);
return res;
}
public void helper(Node root, List<Integer> res) {
if (root == null) {
return;
}
res.add(root.val);
for (Node ch : root.children) {
helper(ch, res);
}
}
}
复杂度分析
- 时间复杂度:O(m),其中 m 为 N 叉树的节点。每个节点恰好被遍历一次。
- 空间复杂度:O(m),递归过程中需要调用栈的开销,平均情况下为 O(logm),最坏情况下树的深度为 m−1,此时需要的空间复杂度为 O(m)。
8.10.3 方法二:迭代
思路
方法一中利用递归来遍历树,实际的递归中隐式调用了栈,在此我们可以直接模拟递归中栈的调用。在前序遍历中,我们会先遍历节点本身,然后从左向右依次先序遍历该每个以子节点为根的子树。
在这里的栈模拟中比较难处理的在于从当前节点 u 的子节点
v
1
v_1
v
1
返回时,此时需要处理节点 u 的下一个节点
v
2
v_2
v
2
,此时需要记录当前已经遍历完成哪些子节点,才能找到下一个需要遍历的节点。在二叉树树中因为只有左右两个子节点,因此比较方便处理,在 N 叉树中由于有多个子节点,因此使用哈希表记录当前节点 u 已经访问过哪些子节点。
- 每次入栈时都将当前节点的 u 的第一个子节点压入栈中,直到当前节点为空节点为止。
- 每次查看栈顶元素 p,如果节点 p 的子节点已经全部访问过,则将节点 p 的从栈中弹出,并从哈希表中移除,表示该以该节点的子树已经全部遍历过;如果当前节点 p 的子节点还有未遍历的,则将当前节点的 p 的下一个未访问的节点压入到栈中,重复上述的入栈操作。
代码
class Solution {
public List<Integer> preorder(Node root) {
List<Integer> res = new ArrayList<Integer>();
if (root == null) {
return res;
}
Map<Node, Integer> map = new HashMap<Node, Integer>();
Deque<Node> stack = new ArrayDeque<Node>();
Node node = root;
while (!stack.isEmpty() || node != null) {
while (node != null) {
res.add(node.val);
stack.push(node);
List<Node> children = node.children;
if (children != null && children.size() > 0) {
map.put(node, 0);
node = children.get(0);
} else {
node = null;
}
}
node = stack.peek();
int index = map.getOrDefault(node, -1) + 1;
List<Node> children = node.children;
if (children != null && children.size() > index) {
map.put(node, index);
node = children.get(index);
} else {
stack.pop();
map.remove(node);
node = null;
}
}
return res;
}
}
复杂度分析
- 时间复杂度:O(m),其中 m 为 N 叉树的节点。每个节点恰好被访问一次。
- 空间复杂度:O(m),其中 m 为 N 叉树的节点。题目中用到哈希表来记录节点的子节点访问记录,哈希表的存储空间等于树的深度,如果 N 叉树的深度为 1 则此时栈与哈希表的空间均为 O(1),如果 N 叉树的深度为 m−1 则此时栈与哈希表的空间为 O(m−1),平均情况下栈与哈希表的空间为 O(logm),因此空间复杂度为 O(m)。
8.20.4 方法三:迭代优化
思路
在前序遍历中,我们会先遍历节点本身,然后从左向右依次先序遍历该每个以子节点为根的子树,此时利用栈先进后出的原理,依次从右向左将子节点入栈,这样出栈的时候即可保证从左向右依次遍历每个子树。参考方法二的原理,可以提前将后续需要访问的节点压入栈中,这样就可以避免记录每个节点的子节点访问数量。
首先把根节点入栈,因为根节点是前序遍历中的第一个节点。随后每次我们从栈顶取出一个节点 u,它是我们当前遍历到的节点,并把 u 的所有子节点从右向左逆序压入栈中,这样出栈的节点则是顺序从左向右的。例如 u 的子节点从左到右为 $v_1, v_2, v_3 $,那么入栈的顺序应当为
v
3
,
v
2
,
v
1
v_3, v_2, v_1
v
3
,
v
2
,
v
1
,这样就保证了下一个遍历到的节点(即 u 的左侧第一个孩子节点
v
1
v_1
v
1
)出现在栈顶的位置。此时,访问第一个子节点
v
1
v_1
v
1
时,仍然按照此方法则会先访问
v
1
v_1
v
1
的左侧第一个孩子节点。
代码
class Solution {
public List<Integer> preorder(Node root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Deque<Node> stack = new ArrayDeque<Node>();
stack.push(root);
while (!stack.isEmpty()) {
Node node = stack.pop();
res.add(node.val);
for (int i = node.children.size() - 1; i >= 0; --i) {
stack.push(node.children.get(i));
}
}
return res;
}
}
复杂度分析
- 时间复杂度:O(m),其中 m 为 N 叉树的节点。每个节点恰好被访问一次。
- 空间复杂度:O(m),其中 m 为 N 叉树的节点。如果 N 叉树的深度为 1 则此时栈的空间为 O(m−1),如果 N 叉树的深度为 m−1 则此时栈的空间为 O(1),平均情况下栈的空间为 O(logm),因此空间复杂度为 O(m)。
8.19.5 my answer—递归
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> children;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, List<Node> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public List<Integer> preorder(Node root) {
List<Integer> ans = new LinkedList<>();
traverse(root,ans);
return ans;
}
void traverse(Node node,List<Integer> ans){
if(node == null)return;
ans.add(node.val);
for(Node child : node.children){
traverse(child,ans);
}
}
}