初稿
标题
0
标题
1
标题
2
3 基于深度路由协议Depth-Based Routing Protocol
在这一章节中,我们详细介绍了DBR路由协议。
3.1 网络架构
如前所述,DBR是可以有效利用多接收器的水下传感器网络架构。图1展示了DBR的示例。在DBR网络中,水面部署多个同时配备射频(radio frequency,RF)和声学调制解调器(acoustic modems)的接收器(Sink node)。带有声学调制解调器(acoustic modems)的水下传感器节点分布在重点关注的水下三维空间中。同时,每个节点都可能是一个数据源(data source)。这些水下传感器节点可以收集数据,还可以将数据中继到接收器。因为所有的接收器(sinks)都有RF调制解调器,所以它们可以通过无线电信道高效地相互通信。因此,如果数据包到达任何接收器(sinks),我们假设它可以高效地传送到其他接收器(sinks)或远程数据中心。这一假设很容易被下事实得到验证:声速(在水中的速度为1.5×10
3
m/s)比电磁波传播速度慢五个数量级(在空气中的传播速度为3×10
8
m/s)。为了关注重点,我们在这篇论文中不考虑水面sink节点的通信。相反,我们假设一个数据包只要成功地传送到水面的某个sink节点,那么这个数据包就被认为到达目的地。
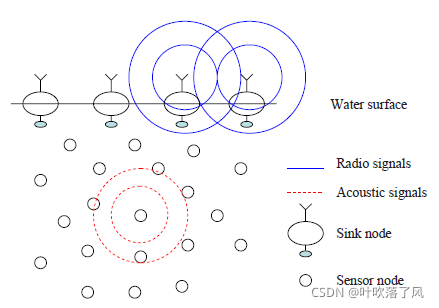
此外,我们假设每个水下节点都知道自身的水下深度信息(即从其自身到水面的垂直距离)。实际上,使用深度传感器可以很容易地获得深度信息。与深度信息相比,水下节点想要获取水下3D空间位置信息就要困难得多。
3.2 协议概述
DBR是一种试图将数据包从源节点(source node)传递到sink节点的贪婪算法。在该过程中,当数据包接近sink节点时,转发节点的深度在减小。如果我们在每个步骤中减少转发节点的深度,则可以将数据包发送到水面(假设不存在“空”区)。
在DBR中,传感器节点(sensor node)根据自己的深度和前一个发送方的深度,分布式地做出数据包转发的决策。上述内容是DBR的关键思想
。
在DBR中,当接收到数据包时,节点首先检索数据包的前一跳的深度d
p
,该跳d
p
嵌入到数据包中。然后,接收节点将其自身的深度d
c
与d
p
进行比较。如果当前节点更靠近水面,即d
c
<d
p
,当前节点将认为自己是转发分组的合格候选。否则,当前节点只会直接丢弃数据包,丢弃的原因是收到的数据包来自更靠近水面的(更好的)节点。接收节点不希望转发该分组。
转发节点的多个相邻节点很可能是在下一跳转发数据包的合格候选节点。如果所有这些合格的节点都尝试广播数据包,将导致高冲突和高能耗。因此,为了减少冲突和能量消耗,需要控制转发节点的数量。此外,由于DBR的继承多路径特性(inherited multiple-path feature)(其中,每个传感器节点以广播的方式使用当前节点所有方向的声学信道(using an omnidirectional acoustic channel)来转发分组),节点可能多次接收相同一个分组。因此,同一个分组可能多次被转发。为了提高能量效率,理想情况下,节点只需发送一次相同的数据包。我们将在下一节讨论抑制冗余数据包的技术。
3.3 路由协议设计
分组格式:
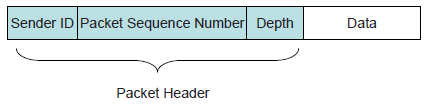
图2展示了DBR的数据包的格式。分组的头部包含三个部分:
- 发送方的ID(Sender ID):源节点的标识符,
- 数据包的序列号:源节点分配给包的唯一序列号,
-
深度:前一个转发节点的深度信息。每个节点在转发数据包时,都要更新深度信息。
抑制冗余数据包:
冗余数据包有两个主要原因:
1.多跳路径(multiple paths)很自然地被选择用于转发数据包;
2.一个节点可能转发同一个数据包多次。
为了节约水下节点的能量和减少数据冲突,需要抑制冗余数据包。虽然在DBR中多跳路径(multiple paths)无法完全消除,但我们使用
优先级队列(priority queue)
来减少转发节点的数量,从而控制转发路径的数量。为了解决第二个问题,DBR使用
数据包历史缓冲区 (packet history buffer)
来保证某个节点在一段时间内只转发同一个数据包一次。
在 DBR 中,每个节点维护一个
优先级队列(priority queue) Q1
和一个
数据包历史缓冲区 (packet history buffer) Q2
。
Q2
中的每一项都是唯一的,且被叫做数据包ID,由Sender ID和Packet Sequence Number组成。当一个节点成功发出数据包时,节点将数据包ID插入到Q2中。 当
Q2
队满时,新的数据包ID将替换最近最少访问 (Least Recently Accessed,LRA) 项目。 换个说法,
Q2
维护节点已经发送的数据包的最少访问历史。
优先级队列(priority queue) Q1
中的每一项由两个组成部分:1.数据包( a packet ),2.数据包的预定发送时间 (the scheduled sending time for the packet)。
Q1
中某项的优先级由预定的发送时间表示。 更具体地说,具有较早发送时间的项目具有较高的优先级。 当一个节点收到一个数据包时,它不是立即发送数据包,而是先将数据包保留一段时间,称为***保持时间 (holding time)*** 。 数据包的预定发送时间 (the scheduled sending time for the packet)是根据节点收到数据包的时间和数据包的保持时间计算得出的。
在一个节点,如果一个传入的数据包之前没有被该节点发送过(即
Q2
中没有这个数据包的ID)并且它是从较低的节点传来(即是从深度更大的节点传来,d
p
> d
c
)。 如果在***保持时间 (holding time)***内再次收到这个数据包,或者新的数据包副本来自更浅深度或相似深度(d
p
≤ d
c
)的节点,则该数据包将从
Q1
中删除,或者其计划发送时间将被更新,如果数据包新副本来自较低的节点(d
p
> d
c
)。 节点按计划发出数据包后,将该数据包从
Q1
中删除,并将其唯一 ID 插入
Q2
。
计算保持时间 (Holding Time Calculation)
如前所述,节点使用
保持时间
来调度数据包的转发。 在节点上,数据包的保持时间是根据d计算的,d 是数据包前一跳的深度与当前节点的深度之间的差值。即使对于相同的数据包,不同深度的节点也会有不同的
保持时间
。 为了减少数据包传到水面的转发路径的跳数,
DBR 尝试选择深度最小的相邻节点作为第一个转发数据包的节点
。 同时,节点还试图阻止其他相邻节点转发相同的数据包以减少能量消耗。
图 3 展示了一个例子。
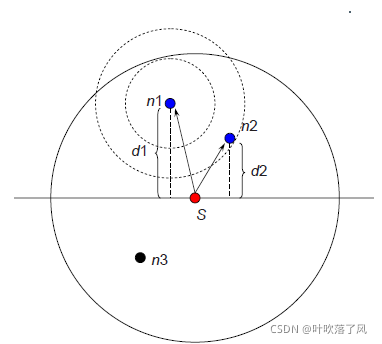
节点
S
(Node S)是数据发送方,节点
n
1
、n
2
、n
3
都是它的一跳邻居节点。 实线圆圈代表节点
S
的传输范围。当节点
S
广播一个数据包时,所有相邻的节点都会收到这个数据包。 节点 n
3
深度大于节点 S,因此n
3
丢弃数据包。 虽然节点 nn
1
和 nn
2
都是合格的转发节点,但节点 n
1
更适合转发数据包。 如果节点 n
2
在它自己计划的数据包发送时间之前收到来自 n1 的数据包,则节点 n
2
会被阻止转发数据包。
根据上述分析,保持时间必须同时满足两个条件:
1.
保持时间
应随着深度
d
的增加而减少;
2.相邻两个节点的保持时间的长短的差别要足够大,使得深度更浅的节点的转发能被对方及时听到(在更深的下层节点开始自己的数据包转发之前监听到)。
以图3为例来展示如何计算
保持时间
。 使用公式1中线性函数
d
来表达
保持时间
,公式中
d
表示当前节点与前一个节点的深度差。
|
f ( d ) = α × d + β f(d)=\alpha \times d +\beta f ( d ) = α × d + β |
(1) |
设
d
1
和
d
2
分别为节点
n
1
和
n
2
处的深度差。假设
n
1
在时间
t
1
收到来自
S
的数据包,
n
2
在时间
t
2
收到数据包,
t
12
是
n
1
和
n
2
之间的传播延迟。之后,这两个条件可以用以下不等式表示:
|
f ( d 1 ) < f ( d 2 ) f(d_{1}) < f(d_{2}) f ( d 1 ) < f ( d 2 ) |
(2) |
和
|
t 1 + f ( d 1 ) + t 12 ≤ t 2 + f ( d 2 ) t_{1}+f(d_{1}) +t_{12}\le t_{2}+f(d_{2}) t 1 + f ( d 1 ) + t 1 2 ≤ t 2 + f ( d 2 ) |
(3) |
将公式(1)带入公式(3)得:
α
≤
(
t
2
−
t
1
)
−
t
12
d
1
−
d
2
,
(
α
<
0
)
\alpha \le \frac{(t_{2}-t_{1})-t_{12}}{d_{1}-d_{2}}, (\alpha <0)
α
≤
d
1
−
d
2
(
t
2
−
t
1
)
−
t
1
2
,
(
α
<
0
)
上述不等式中的α是负数。只有当
∣
α
∣
≥
(
t
2
−
t
1
)
−
t
12
d
1
−
d
2
| \alpha | \ge \frac{(t_{2}-t_{1})-t_{12}}{d_{1}-d_{2}}
∣
α
∣
≥
d
1
−
d
2
(
t
2
−
t
1
)
−
t
1
2
时,公式(2)和公式(3)才能被满足。 考虑到n
1
和n
2
可能处于最不佳的位置,我们设定
α
=
2
τ
d
1
−
d
2
\alpha =\frac{2\tau }{d_{1}-d_{2}}
α
=
d
1
−
d
2
2
τ
τ
=
R
v
0
\tau =\frac{R}{v_{0}}
τ
=
v
0
R
上述公式中,τ是一跳的最大传播时延,R是一个声呐节点的最大传输距离,v
0
是水中的声速。
α的数值取决于两个节点n
1
和n
2
的深度差(d
1
-d
2
)。对于一个节点的下一跳邻居,α的数值在[0,R]范围内变化,R是一个节点的最大传输距离。
|
当 ( d 1 − d 2 ) ⟶ 0 时 , α ⟶ − ∞ 。 当(d_{1} – d_{2}) \longrightarrow 0 时, \alpha \longrightarrow – \infty 。 当 ( d 1 − d 2 ) ⟶ 0 时 , α ⟶ − ∞ 。 |
(a) |
公式(a)表明我们无法找到一个常数α来让公式(2)总是成立。因此,我们使用一个
全局常量δ
来替代(d
1
-d
2
)进行
保持时间
的计算。因此,
α
=
−
2
τ
δ
\alpha = – \frac{2\tau}{\delta}
α
=
−
δ
2
τ
如果(d
1
-d
2
)≥δ,那么节点n
1
将先发送一个抑制节点n
2
发送数据的控制包。
假设最小深度的节点的
保持时间
是0. β可以通过下列公式计算:
|
− 2 τ δ R + β = 0 -\frac{2\tau}{\delta}R+\beta =0 − δ 2 τ R + β = 0 |
|
{自己的理解:假设图3中S坐标(0,0),n 1 的坐标是(0,R),且n 1 位于最小深度,随后将{d=R,f(d)=0}带入公式(1)中。 β = 2 τ δ R \beta = \frac{2\tau}{\delta}R β = δ 2 τ R } |
将计算出来的α和β带入公式(1)中,得到f(d)的定义:
f
(
d
)
=
2
τ
δ
×
(
R
−
d
)
,
δ
∈
(
0
,
R
]
f(d) =\frac{2\tau}{\delta}\times(R-d),\delta \in (0,R]
f
(
d
)
=
δ
2
τ
×
(
R
−
d
)
,
δ
∈
(
0
,
R
]
使用不同的δ,网络将有不同的性能。当δ较小时,节点的
保持时间
将较长(如何它们和前一个节点的的深度差不完全等于R),这也许会导致较长的端到端时延。同时,这些节点的转发更有可能被更靠近水面的相邻节点的转发所抑制,从而导致更低的能耗。
深度阈值
为了更好地控制参与数据包转发的节点数量,我们在DBR中引入了另一个全局参数
Depth Threshold dth
。 只有当数据包的前一跳深度 d
p
与当前节点的深度 d
c
之间的差值大于阈值 d
th
时,节点才会转发数据包。 d
th
可以是正数、0 或负数。 如果 d
th
设置为 0,则所有深度小于当前节点的节点都是合格的转发候选。 如果 d
th
设置为 -R(R 是传感器节点的最大传输范围),则 DBR 成为泛洪协议。
总结
DBR算法如下所示:

算法解释:
节点接收到数据包后,首先根据深度信息和深度阈值d
th
检查自己是否是该数据包的合格转发者。
如果它不是合格的转发节点,它会在 Q
1
中搜索数据包并删除具有相同数据包 ID 的数据包,因为另一个(更好的)节点已经转发了该数据包。
如果节点是合格的转发器,它会在包历史缓冲区 Q
2
中搜索包。 如果在 Q
2
中找到该数据包,则将其丢弃,因为它最近已被转发。
否则,节点根据当前系统时间和保持时间计算数据包的发送时间,并将数据包插入优先级队列Q
1
。 注意如果数据包已经在Q
1
,发送时间会更新到最小的时间。
稍后,Q
1
中排队的数据包将根据其预定的发送时间发送出去。
4 算法评估
在这一章节,我们将评估DBR的表现,并把它与Vector Based forwarding(VBF) protocol进行比较。
4.1 模拟环境设置