-
平衡二叉树的定义(AVL)定义
平衡二叉树或者是一棵空树,或者满足以下的性质:它的左子树和右子树的高度之差的绝对值不超过1,并且左子树和右子树也是一个平衡二叉树。 -
平衡因子
左子树高度减去右子树的高度的值或者右子树高度减去左子树高度的值。显然 -1 <=bf <= 1 -
AVL树的引入
平衡二叉树在二叉排序树上引入的,在二叉树中,如果插入的节点接近有序,那么二叉树就会退化为链表大大降低了查找效率,为了使二叉树无论什么情况下最大限度的接近满二叉树,从而保证它的查找效率,因此引入平衡二叉树。 -
AVL树的实现
如何保证二叉树在任何情况下都能最大限度接近满二叉树,从而保证它的查找效率呢?那就是旋转,当平衡因子的绝对值大于1的时候,我们就需要对其进行旋转。 -
旋转步骤详解
我们只需要理清需要旋转的情况,掌握旋转的要素,找到其中的规律,就能轻松地写出AVL树的代码了,下面我详细的给出旋转的情况与步骤,大家仔细观察找出其中的规律。(
此例中的平衡因子bf采用的是右子树的高度减去左子树的高度
)
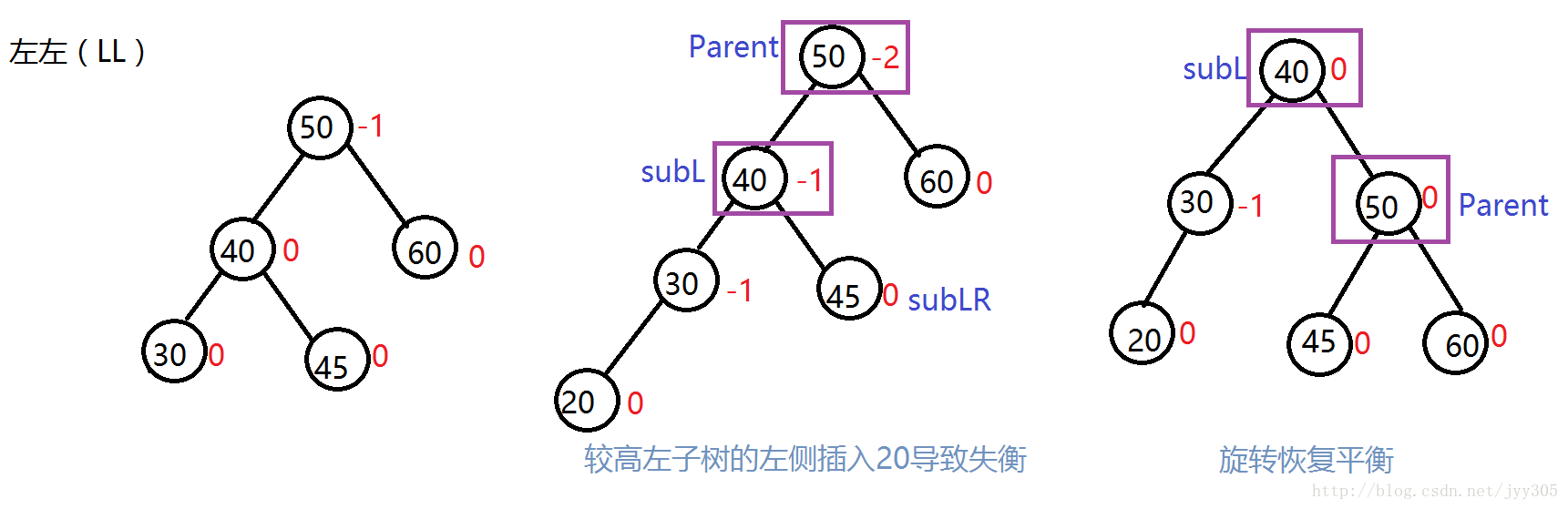
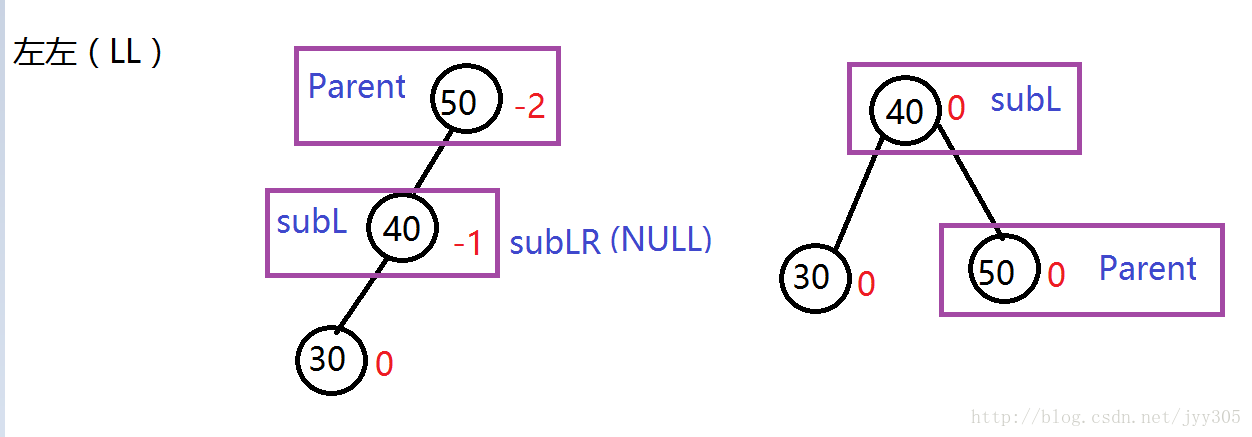
左左(LL)(右旋)
针对于在较高左子树的左侧插入节点的这种情况大家发现了什么规律呢?我们发现在插入之前Parent是离插入节点最近有可能失衡的节点,对于LL的三种情况我们发现插入节点导致失衡后图示(Parent) 节点平衡因子为-2,他的左孩子(SubL)为-1,进行右旋了之后Parent 以及 SubL节点的平衡因子都变成了0。通过这些规律我们来实现右旋的代码
右旋操作代码
void rRotate(Node *Parent)//LL
{
Node *subL = Parent->_pLeft;
Node *subLR = subL->_pRight;
Parent->_pLeft = subLR;
if (subLR)//左单支
subLR->_parent = Parent;
subL->_pRight = Parent;
Node *pParent = Parent->_parent;
Parent->_parent = subL;
subL->_parent = pParent;
if (NULL == pParent)//Parent是根节点
_pRoot = subL;
else if (Parent == pParent->_pLeft)
pParent->_pLeft = subL;
else
pParent->_pRight = subL;
//修改平衡因子
subL->_bf = 0;
Parent->_bf = 0;
}
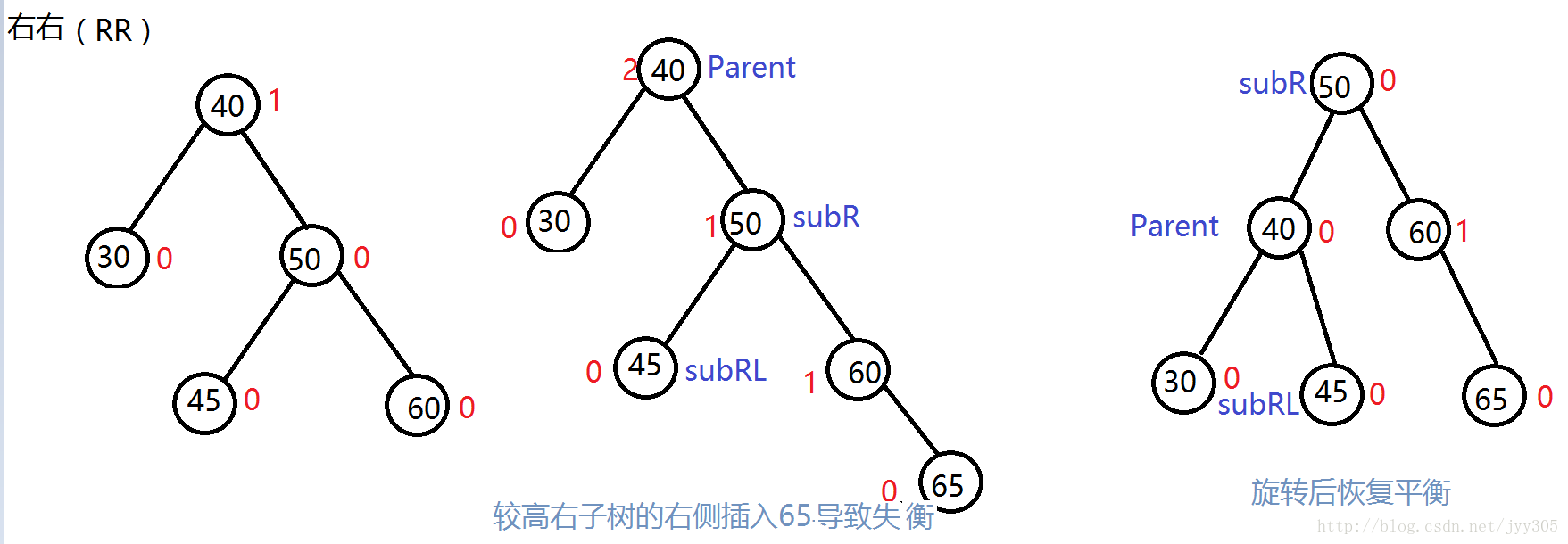
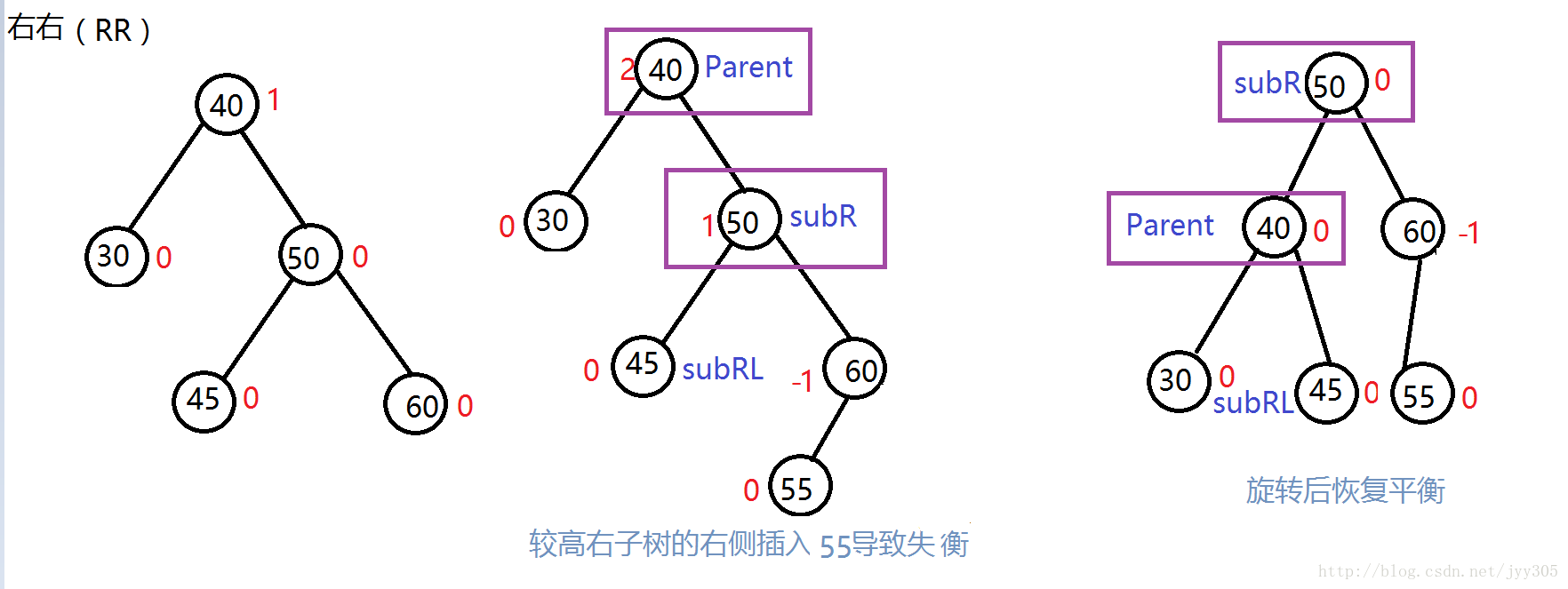
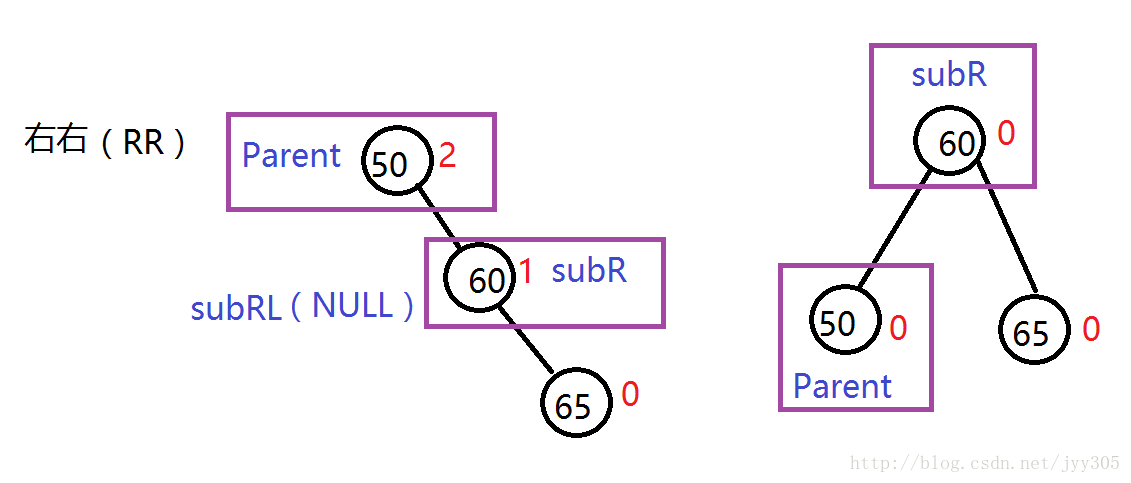
右右(RR)左旋
针对于在较高右子树的右侧插入节点的这种情况大家发现了什么规律呢?我们发现在插入之前Parent是离插入点最近有可能失衡的节点,对于RR的三种情况我们发现插入节点导致失衡后图示(Parent) 节点平衡因子为2,他的右孩子(SubR)为1,进行左旋了之后Parent 以及 SubR节点的平衡因子都变成了0。通过规律写出RR情况左旋的代码。
void lRotate(Node *Parent)//RR
{
Node *subR = Parent->_pRight;
Node *subRL = subR->_pLeft;
Parent->_pRight = subRL;
if (subRL)
subRL->_parent = Parent;
subR->_pLeft = Parent;
subR->_parent = Parent->_parent;
Parent->_parent = subR;
Node *pParent = subR->_parent;
if (NULL == pParent)
_pRoot = subR;
else if (Parent == pParent->_pLeft)
pParent->_pLeft = subR;
else
pParent->_pRight = subR;
Parent->_bf = 0;
subR->_bf = 0;
}
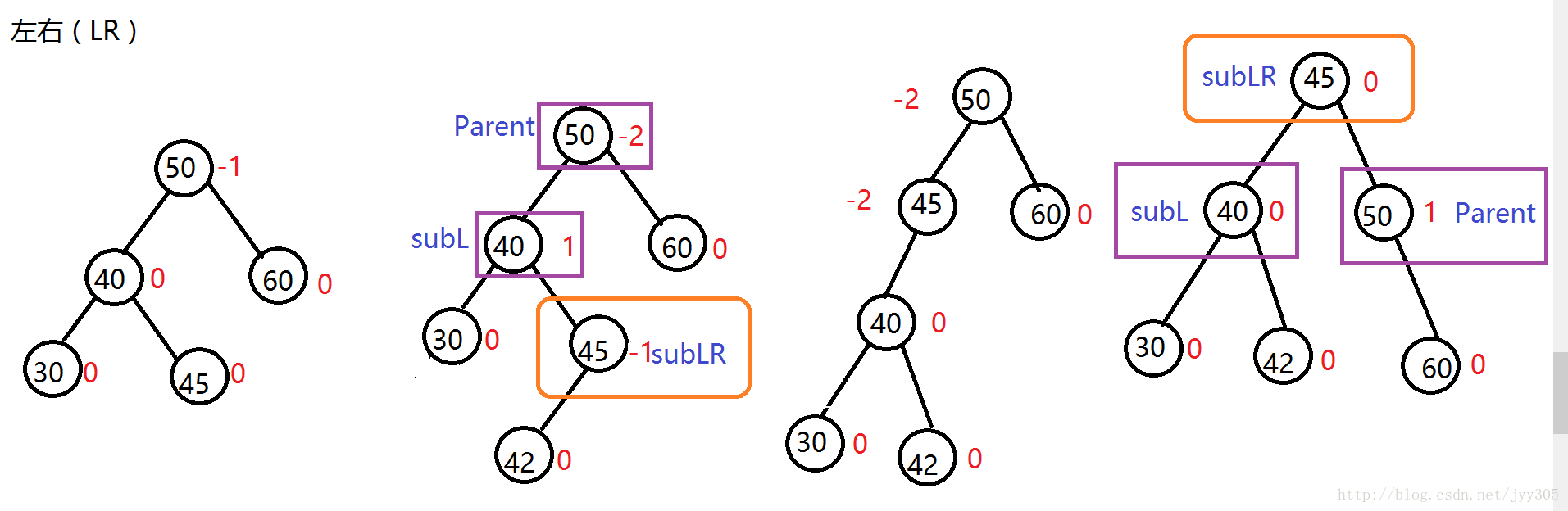
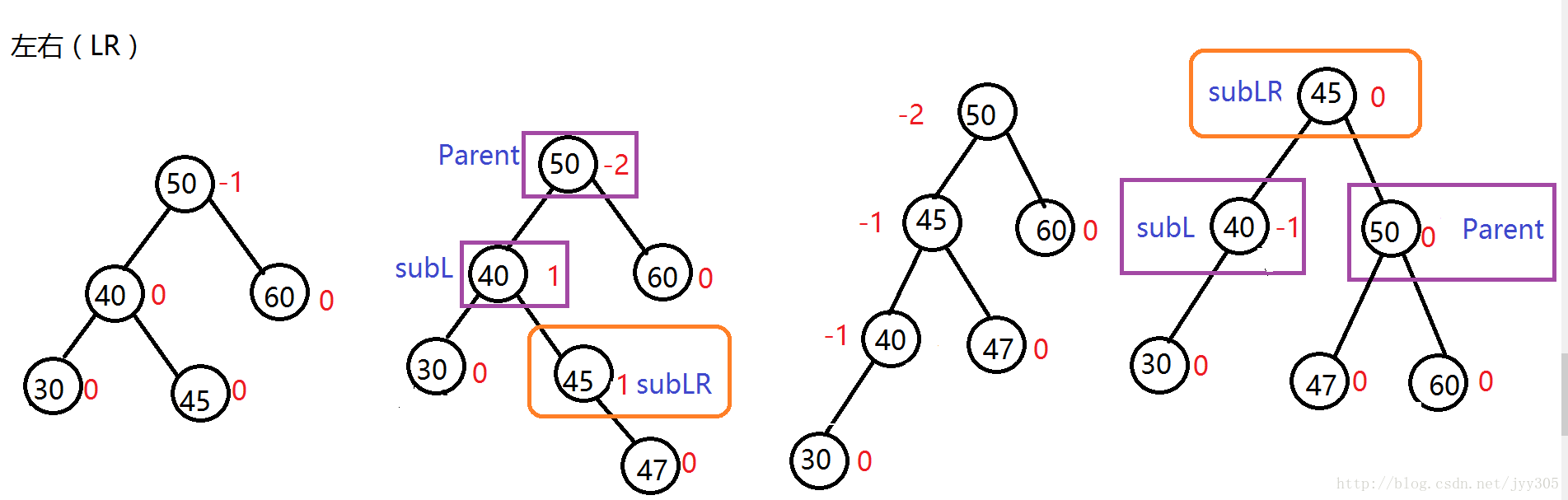
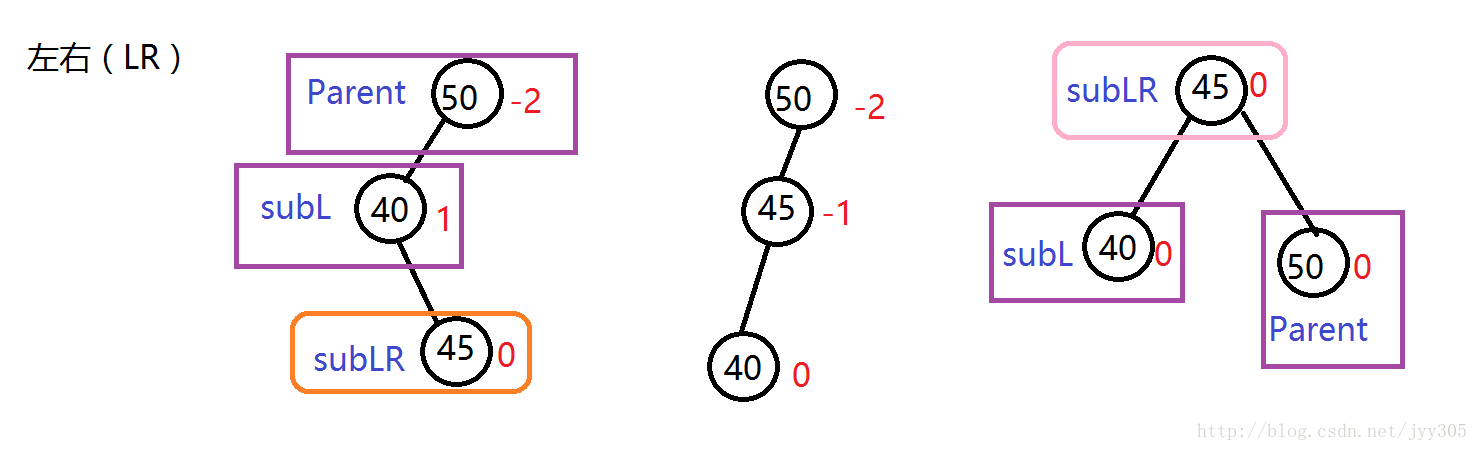
左右(LR)
针对于在较高左子树的右侧插入节点的这种情况大家发现了什么规律呢?我们发现在插入之前Parent是离插入点最近有可能失衡的节点,对于LR的三种情况我们发现插入节点导致失衡后图示(Parent) 节点平衡因子为-2,他的左孩子(SubL)为1,插入及旋转发现旋转之前SubLR为-1,旋转之后Parent为1,SubLR为0,旋转之前SubLR为1,旋转之后SubL为-1,SubLR为0,通过规律写出LR情况左旋的代码。
void lrRotate(Node *Parent)//LR
{
Node *subL = Parent->_pLeft;
Node *subLR = subL->_pRight;
int bf = subLR->_bf;
lRotate(Parent->_pLeft);
rRotate(Parent);
if (1 == bf)
subL->_bf = -1;
else if (-1 == bf)
Parent->_bf = 1;
subLR->_bf = 0;
}
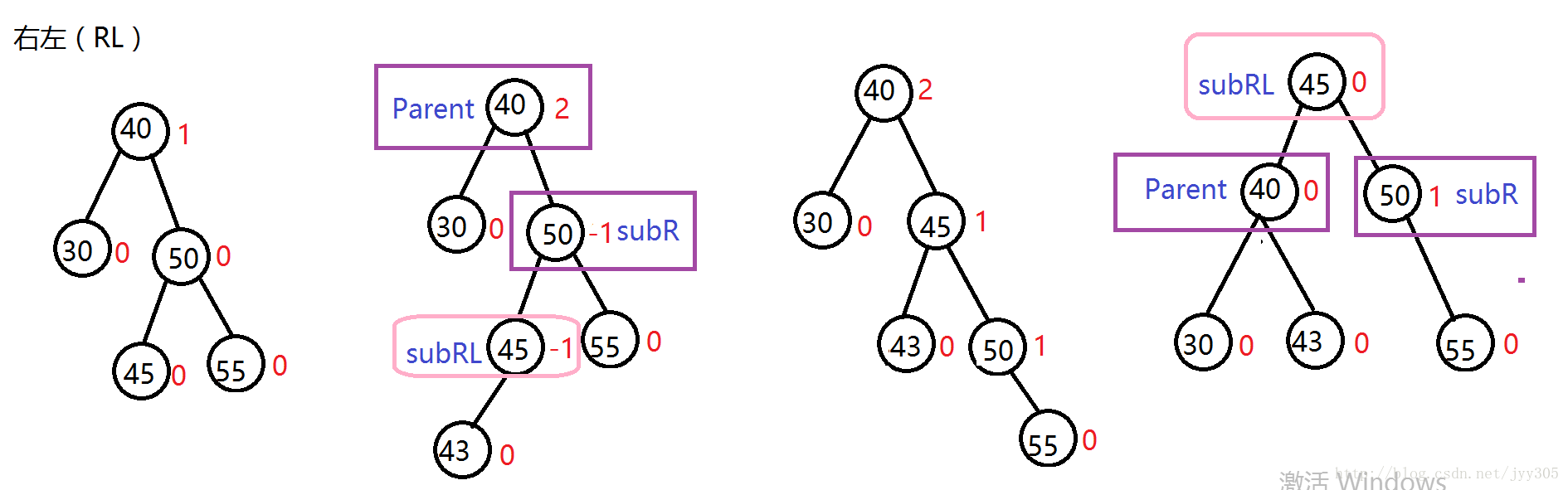
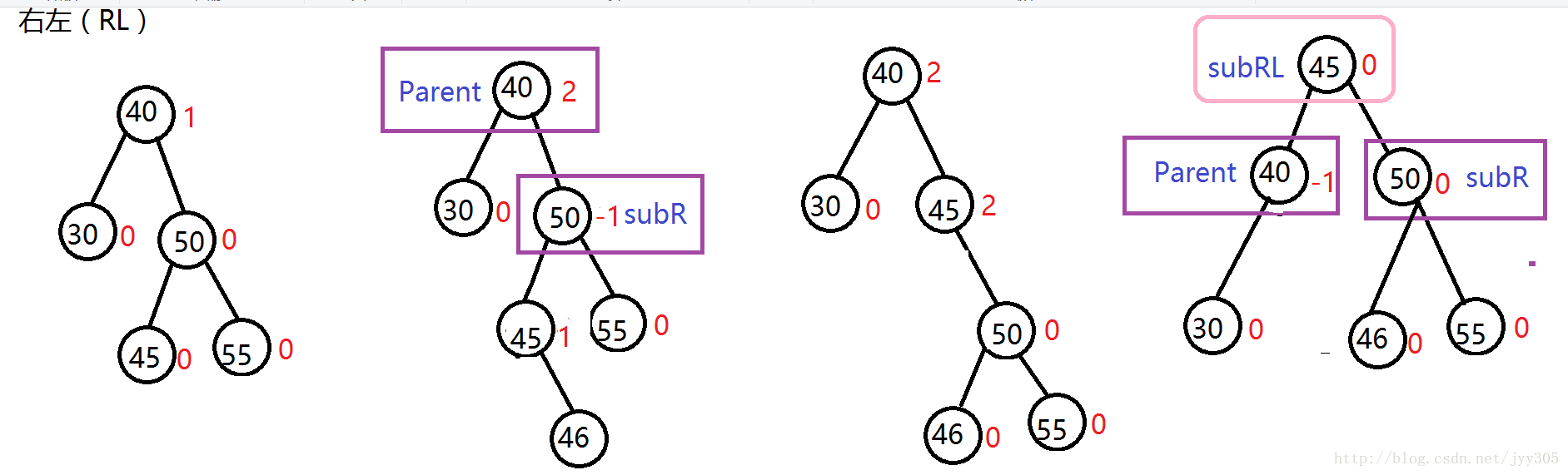
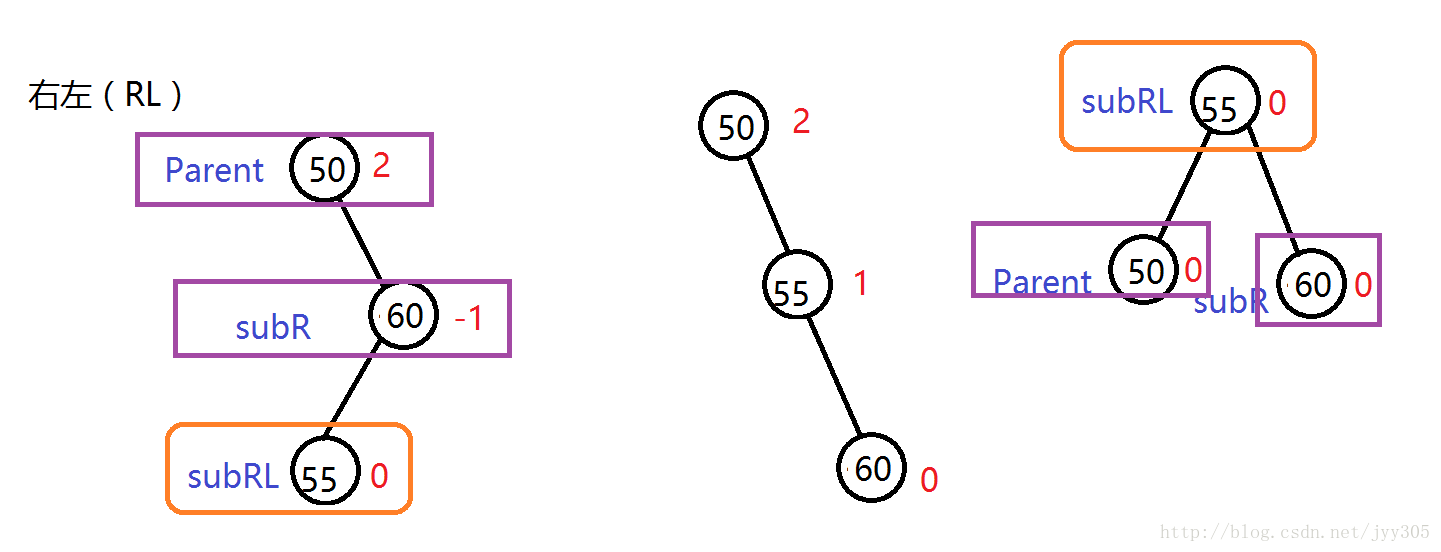
右左(RL)
针对于在较高右子树的左侧插入节点的这种情况大家发现了什么规律呢?我们发现在插入之前Parent是离插入点最近有可能失衡的节点,对于RL的三种情况我们发现插入节点导致失衡后图示(Parent) 节点平衡因子为2,他的右孩子(SubR)为-1,插入及旋转发现旋转之前SubLR为-1,旋转之后SubR为1,SubLR为0,旋转之前SubRL为1,旋转之后Parent为-1,SubLR为0,通过规律写出RL情况的代码。
void rlRotate(Node *Parent)
{
Node *subR = Parent->_pRight;
Node *subRL = subR->_pLeft;
int bf = subRL->_bf;
rRotate(Parent->_pRight);
lRotate(Parent);
if (1 == bf)
Parent->_bf = -1;
else if (-1 == bf)
subR->_bf = 1;
subRL->_bf = 0;
}
综上我们不难总结出AVL树插入的规律

- AVL树插入代码
bool Insert(const K& key, const V& value)
{
Node *pNew = new Node(key,value);
Node *pCur = _pRoot;
Node *parent = NULL;
if (NULL == _pRoot)
{
_pRoot = pNew;
return true;
}
while (pCur)//寻找插入位置
{
if (key < pCur->_key)
{
parent = pCur;
pCur = pCur->_pLeft;
}
else if (key > pCur->_key)
{
parent = pCur;
pCur = pCur->_pRight;
}
else
return false;
}
if (key < parent->_key)//插入元素
parent->_pLeft = pNew;
else
parent->_pRight = pNew;
pNew->_parent = parent;
//修改平衡因子
while (parent)
{
if (pNew == parent->_pLeft)
parent->_bf--;
else
parent->_bf++;
if (0 == parent->_bf)
return true;
else if (1 == parent->_bf || -1 == parent->_bf)
{
pNew = parent;
parent = parent->_parent;
}
else//2需要进行旋转
{
if (-2 == parent->_bf && -1 == pNew->_bf)//LL
rRotate(parent);
else if (2 == parent->_bf && 1 == pNew->_bf)//RR
lRotate(parent);
else if (-2 == parent->_bf && 1 == pNew->_bf)//LR
lrRotate(parent);
else if (2 == parent->_bf && -1 == pNew->_bf)//RL
rlRotate(parent);
return true;
}
}
return true;
}
完整代码请戳
https://coding.net/u/Hyacinth_Dy/p/MyCode/git/blob/master/AVLBinaryTree