二叉树的几种遍历方法及递归和非递归的实现

遍历二叉树是按照指定的路径方式访问树中的每一个节点且仅访问一次，

二叉树一般有4种遍历方法：前(先)序遍历、中序遍历、后序遍历和层次(分层)遍历

。

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

层次遍历：先遍历第1层，接着遍历第2层，…遍历第k层…，每层按从左到右的顺序遍历

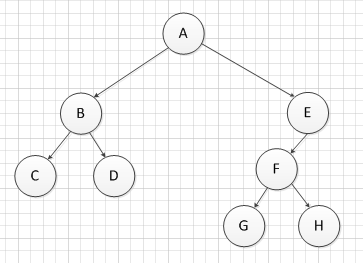
这里写图片描述

上图的树结构中的4种遍历方法的结果为

前序遍历：ABCDEFGH

中序遍历：CBDAGFHE

后序遍历：CDBGHFEA

层次遍历：ABECDFGH

接着来看看这4种遍历方法的递归实现

树的节点的定义

#include <iostream>
#include <stack>
#include <queue>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>

using std::cin;
using std::cout;
using std::endl;
using std::stack;
using std::queue;

typedef struct binary_tree_node
{
    int elem;
    binary_tree_node *left;
    binary_tree_node *right;
}binary_tree_node,*binary_tree;

1.前序遍历

//前(先)序遍历递归实现
void PreOrderTraverse_Recursive(binary_tree root)
{
    if(NULL!=root)
    {
        cout<<root->elem<<" ";
        PreOrderTraverse_Recursive(root->left);
        PreOrderTraverse_Recursive(root->right);
    }
}

2.中序遍历

//中序遍历递归实现
void InOrderTraverse_Recursive(binary_tree root)
{
    if(NULL!=root)
    {
        InOrderTraverse_Recursive(root->left);
        cout<<root->elem<<" ";
        InOrderTraverse_Recursive(root->right);
    }
}

3.后序遍历

//后序遍历递归实现
void PostOrderTraverse_Recursive(binary_tree root)
{
    if(NULL!=root)
    {
        PostOrderTraverse_Recursive(root->left);
        PostOrderTraverse_Recursive(root->right);
        cout<<root->elem<<" ";
    }
}

4.层次遍历

这里层次遍历的递归实现不知道怎么写？求帮助

接着看下这4种遍历方法的非递归遍历

1.前(先)序遍历

//前(先)序遍历非递归实现
void PreOrderTraverse(binary_tree root)
{
    if(NULL!=root)
    {
        stack<binary_tree> s;
        binary_tree pTempNode;
        s.push(root);
        while(!s.empty())
        {
            pTempNode=s.top();
            cout<<pTempNode->elem<<" ";
            s.pop();
            if(NULL!=pTempNode->right)
                s.push(pTempNode->right);
            if(NULL!=pTempNode->left)
                s.push(pTempNode->left);
        }
    }
}

2.中序遍历

//中序遍历非递归实现方法1
void InOrderTraverse_1(binary_tree root)
{
    if(NULL!=root)
    {
        stack<binary_tree> s;

        s.push(root);
//        binary_tree pTempNode=root;
//        while(!s.empty())  //单独判断s是否为空可能导致只输出遍历结果的前部分序列
        binary_tree pTempNode=root->left;
        while(NULL!=pTempNode||!s.empty()) //需要添加判断pTempNode是否为空
        {
            if(NULL!=pTempNode)
            {
                s.push(pTempNode);
                pTempNode=pTempNode->left;
            }
            else
            {
                pTempNode=s.top();
                cout<<pTempNode->elem<<" ";
                s.pop();
                pTempNode=pTempNode->right;
            }
        }
    }
}

//方法2，基本与方法1相同
void InOrderTraverse_2(binary_tree root)
{
    if(NULL!=root)
    {
        stack<binary_tree> s;
        s.push(root);
        binary_tree pTempNode=root->left;
        while(NULL!=pTempNode||!s.empty())
        {
            while(NULL!=pTempNode)
            {
                s.push(pTempNode);
                pTempNode=pTempNode->left;
            }
            if(!s.empty())
            {
                pTempNode=s.top();
                cout<<pTempNode->elem<<" ";
                s.pop();
                pTempNode=pTempNode->right;
            }
        }
    }
}

//方法3
void InOrderTraverse_3(binary_tree root)
{
    if(NULL!=root)
    {
        stack<binary_tree> s;
        binary_tree pTempNode;
        s.push(root);
        while(!s.empty())
        {
            pTempNode=s.top();
            while(NULL!=pTempNode)
            {
                s.push(pTempNode->left);
                pTempNode=s.top();
            }
            s.pop();   //空节点出栈
            if(!s.empty())
            {
                pTempNode=s.top();
                cout<<pTempNode->elem<<" ";
                s.pop();
                //右子树节点入栈
                s.push(pTempNode->right);
            }
        }
    }
}

3.后序遍历

//后序遍历非递归实现方法1
void PostOrderTraverse_1(binary_tree root,int Len) //Len为树的节点总数
{
    if(NULL!=root&&Len)
    {
        stack<binary_tree> s;
        s.push(root);
        binary_tree pTempNode=root->left;
        char *Flag=(char*)malloc(sizeof(char)*Len);  //Flag作为是否访问的标志位；0表示还没有访问，1表示访问成功
        while(!s.empty())
        {
            while(NULL!=pTempNode)
            {
                s.push(pTempNode);
                Flag[s.size()]=0;  //标记未访问
                pTempNode=pTempNode->left;
            }
            while(!s.empty()&&Flag[s.size()]==1)
            {
                pTempNode=s.top();
                s.pop();
                cout<<pTempNode->elem<<" ";
            }
            //从右子树开始遍历
            if(!s.empty())
            {
                pTempNode=s.top();
                Flag[s.size()]=1;  //登记访问了
                pTempNode=pTempNode->right;
            }
            else
                break;
        }
    }
}

//方法2
void PostOrderTraverse_2(binary_tree root) //每次压入1个节点时压入2次
{
    stack<binary_tree> s;
    s.push(root),s.push(root);
    while(!s.empty())
    {
        binary_tree curr=s.top();
        s.pop();
        if(!s.empty()&&curr->elem==s.top()->elem)
        {
            if(curr->right)
                s.push(curr->right),s.push(curr->right);
            if(curr->left)
                s.push(curr->left),s.push(curr->left);
        }
        else
        {
            cout<<curr->elem<<" ";
        }
    }
}

//方法3
void PostOrderTraverse_3(binary_tree root)
{
    stack<binary_tree> s;
    s.push(root);
    binary_tree prev;
    while(!s.empty())
    {
        binary_tree pTempNode=s.top();
        s.pop();
        if((pTempNode>left==NULL&&pTempNode>right==NULL)||prev==pTempNode->right||(prev==pTempNode->left&&pTempNode->right==NULL))
        {
            cout<<pTempNode->elem<<" ";
            prev=pTempNode;
        }
        else
        {
            s.push(pTempNode);
            if(pTempNode->right!=NULL)
                s.push(pTempNode->right);
            if(pTempNode->left!=NULL)
                s.push(pTempNode->left);
        }
    }
}

//方法4
void PostOrderTraverse_4(binary_tree root)
{
    if(NULL!=root)
    {
        stack<binary_tree> s;
        s.push(root);
        binary_tree prev=NULL;  //prev指向前(上)一次遍历的节点
        while(!s.empty())
        {
            binary_tree curr=s.top();   //curr是当前栈的栈顶元素，指向当前要遍历的节点
            if(!prev||prev->left==curr||prev->right==curr)
            {
                if(curr->left)
                    s.push(curr->left);
                else if(curr->right)
                    s.push(curr->right);
                else
                {
                    cout<<curr->elem<<" ";
                    s.pop();
                }
            }
            else if(curr->left==prev)
            {
                if(curr->right)
                    s.push(curr->right);
                else
                {
                    cout<<curr->elem<<" ";
                    s.pop();
                }
            }
            else if(curr->right==prev)
            {
                cout<<curr->elem<<" ";
                s.pop();
            }
            prev=curr;
        }
    }
}

//方法4的简化版
void PostOrderTraverse_4_Easier(binary_tree root)
{
    if(NULL!=root)
    {
        stack<binary_tree> s;
        s.push(root);
        binary_tree prev=NULL;
        while(!s.empty())
        {
            binary_tree curr=s.top();
            if(!prev||prev->left==curr||prev->right==curr)
            {
                if(curr->left)
                    s.push(curr->left);
                else if(curr->right)
                    s.push(curr->right);
            }
            else if(curr->left==prev)
            {
                if(curr->right)
                    s.push(curr->right);
            }
            else
            {
                cout<<curr->elem<<" ";
                s.pop();
            }
            prev=curr;
        }
    }
}

//方法5
void PostOrderTraverse_5(binary_tree root)  //用2个栈实现
{
    if(NULL!=root)  //对于第1个栈，先压入根节点并立即弹出压入第2个栈中
    {               //剩下的先后压入左、右孩子节点，并弹出压入第2个栈中
        stack<binary_tree> s;
        stack<binary_tree> output;
        s.push(root);
        while(!s.empty())
        {
            binary_tree curr=s.top();
            output.push(curr);
            s.pop();
            if(curr->left)
                s.push(curr->left);
            if(curr->right)
                s.push(curr->right);
        }
        while(!output.empty())
        {
            cout<<output.top()->elem<<" ";
            output.pop();
        }
    }
}

4.层次遍历

//层次遍历非递归实现
void LevelTraversal(binary_tree root)
{
    if(NULL!=root)
    {
        queue<binary_tree> s;
        s.push(root);
        binary_tree pTempNode;
        while(!s.empty())
        {
            pTempNode=s.front();
            cout<<pTempNode->elem<<" ";
            s.pop();
            if(NULL!=pTempNode->left)
                s.push(pTempNode->left);
            if(NULL!=pTempNode->right)
                s.push(pTempNode->right);
        }
    }
}

【注：】

深度遍历的运行过程是先进后出的，自然的方法是栈和递归；广度遍历的运行过程是先进先出的，自然的方法是队列

创建二叉树

//创建二叉树
void CreateBinaryTree(binary_tree root)
{
    if(NULL!=root)
    {
        int elem;
        cin>>elem;
        root->elem=elem;
        char c;
        if((c=getchar())=='#')
        {
            root->left=NULL;
            root->right=NULL;
        }
        else
        {
            root->left=(binary_tree)malloc(sizeof(binary_tree_node));
            root->right=(binary_tree)malloc(sizeof(binary_tree_node));
        }

        CreateBinaryTree(root->left);
        CreateBinaryTree(root->right);
    }
}

求二叉树的节点总数

//求二叉树的节点总数
int CountBinaryTree(binary_tree root)
{
    if(NULL!=root)
    {
        return (CountBinaryTree(root->left)+CountBinaryTree(root->right)+1);
    }
    else
        return 0;
}

最后进行测试

//主代码测试
int main()
{
    binary_tree root=(binary_tree)malloc(sizeof(binary_tree_node));
    CreateBinaryTree(root);

    PreOrderTraverse_Recursive(root);
    cout<<endl;
    PreOrderTraverse(root);
    cout<<endl<<endl;

    InOrderTraverse_Recursive(root);
    cout<<endl;
    InOrderTraverse_1(root);
    cout<<endl;
    InOrderTraverse_2(root);
    cout<<endl;
    InOrderTraverse_3(root);
    cout<<endl<<endl;

    PostOrderTraverse_Recursive(root);
    cout<<endl;
    PostOrderTraverse_1(root,CountBinaryTree(root));
    cout<<endl;
    PostOrderTraverse_2(root);
    cout<<endl;
    PostOrderTraverse_3(root);
    cout<<endl;
    PostOrderTraverse_4(root);
    cout<<endl;
    PostOrderTraverse_5(root);
    cout<<endl<<endl;

    LevelTraversal(root);

    return 0;
}

输入二叉树如下

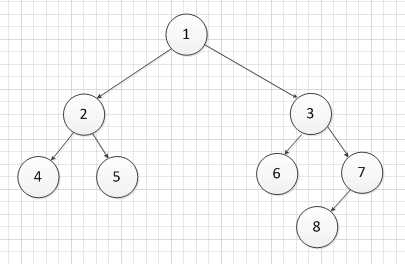
这里写图片描述

测试结果为

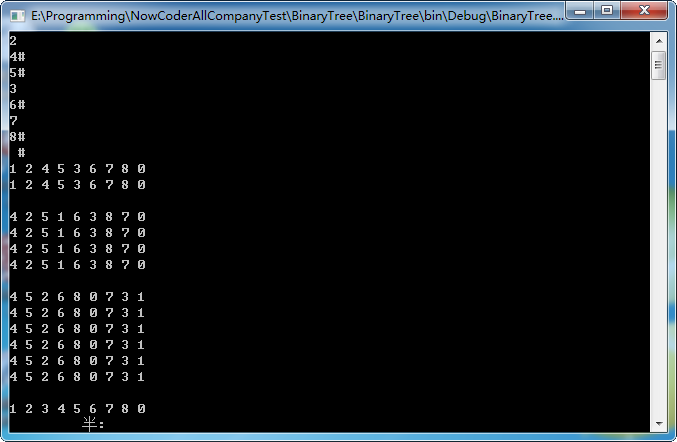
这里写图片描述

从上面的测试结果可知，前(先)、中、后序遍历的递归和非递归实现和层次遍历的非递归实现是符合预期的。创建二叉树时原本节点7的右子树是没有的，但在创建时自己以‘ ’+‘#’(空格+井号)结束输入，为什么最后节点7的右子树节点会默认为0？求各位帮忙解答

参考资料

原文链接：https://blog.csdn.net/g360z247j123/article/details/51872425

你可能也喜欢