沿着极线搜索下来,得到一个匹配得分沿着距离的分布,会有很多峰值,真实的对应点只有一个:
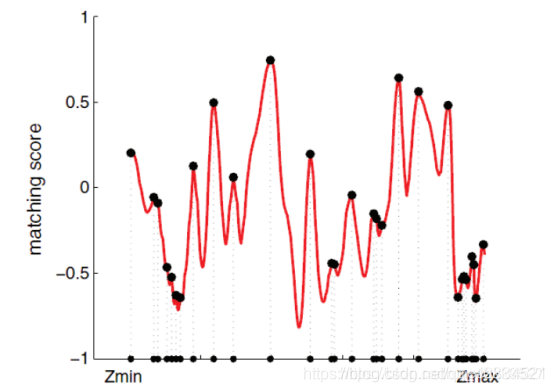
显然这个分布里面,中间有个凸起的点特别高,那直接选它在图像上的位置当投影点不就完事了?
是这样的,但是,某个像素点的深度分布随着相机的不断运动,也就是不断接收到新的数据以后,是会不断变化的。(当然上面那个图是不会变的,因为那是两张图像顺着极线比较下来得到的。注意一个理解:上面的折线图并不是深度的分布,而是左图的一个点,在右图上沿着极线匹配得分的分布。一旦确定了一个投影点,咔嚓直接连线就得到一个深度了。但是随着新的数据的到来一个点不可能只被拍摄到两次,根据之后拍摄到的点算出的深度,很有可能不符合这里的情况的。(也就是利用不同的图像算块匹配,得到不同的上面的红色折线图,选最大的地方连线,求出的点的世界坐标,换算到之前的测量结果下,可能深度是不一致的。换言之,A位置算出m点的深度是5,之后根据新的数据算,算出之前在A位置这里m点的深度不应该是5了。所以深度有很多种可能性,这些可能性是应该是满足一个分布的)。
设像素的深度满足分布:
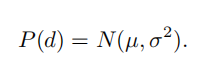
新到的数据满足分布:
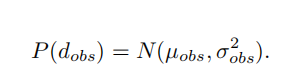
两个概率应该相乘,因为是要同时满足这些数据的测量,那么两个正态分布相乘,结果还是正态分布,均值和方差长这样:
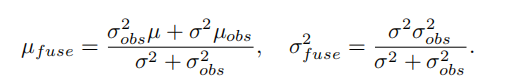
看到这里觉得十分的抽象,不知道这些代表什么含义。我在下面会进行介绍:
高斯分布的深度滤波器:
到这里之前,高博书里讲的还算靠谱的,虽然在深度分布那块可能还有些欠缺,起码是没有错误的。之后他想表示一下位置对于深度不确定性的影响。他画了一个不确定性分析图,基于这个图进行推导:
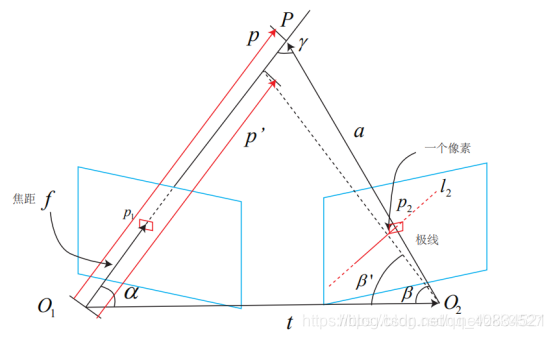
基于这个图推导的话是有问题的:首先O1p1并不是焦距。这应该只是一个近似。因为焦距的定义应该是光心距离成像平面的垂直距离,不可能光心距离成像平面上的每个点的距离都是焦距f。不过这倒不是大碍,原因有二:第一,它应该是很近似的,实际的成像平面应该是很小的而不是洗出来的照片那么大。第二,就算不是焦距,焦距是知道的,p1的位置也是知道的,根据三角形勾股定理也能算出O1p1的值,因此我倾向于把这个距离值当成是f,并没有说是焦距f的意思。
之后:β’=β+δβ,很显然这里给写反了,应该是β’=β-δβ。(当然加减都是可以的,按书上的图来说应该是减)
此外,咖马γ应该是p’与虚线的夹角。
在δβ的值的推导的时候,用到了焦距的定义,说δβ=arctan1/f,这应该强调是一个近似,换成约等号,两个角都接近90度,那个小角δβ比较小,才能这么近似去算。
因此这块不用深究,因为之后把β和β‘搞混掉了。不过关系不大,咱们自己纠正对就行了:
步骤为:
a = p – t
α = arccos<p, t>
β = arccos<a, -t>
δβ=arctan1/f
β’= β-δβ
γ=π-α -β
σobs=||p||-||p’||
总之意思是,一旦有δβ的像素误差,就会造成p和p‘之间的差异。两个深度向量的1范数之差定义为σobs,作为一个像素误差带来的深度不确定度。(显然这个不确定度σobs是可以直接通过如下方式算出来的:根据前面的红色折线图,找到分值最大的点,连线求出深度,得到一个坐标系下的点;它左右稍微有点误差的情况下连线算出的深度,又得到一个点;两个深度的1范数之差就是σobs。不过这是实际意义上的联系,实际计算方法还是按上面列的几个公式来计算)
再来回顾一下上面的高斯分布的均值和方差:
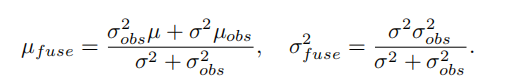
μobs实际上就是每次我们新三角化出来的深度值,而对于σobs2,就是上面提到的 不确定度σobs。
第一次三角化出来的μ,σ2就可以作为初始值,然后每次新三角化出一个三维点,就去更新深度值的分布。
深度滤波器的现实意义就是不断缩小这个不确定度。缩小不确定度是通过如下方式进行的:不断求出三维点的坐标,更新这个分布,直到这个分布的不确定性小于你希望的阈值,就认为是收敛了,收敛以后的均值,就不再改动了,当做是你确定下来的深度值。