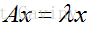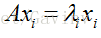最近在查看CNN相关文章的时候遇到了一个问题,就是矩阵的奇异值分解问题。虽然在本科的时候学过了矩阵的特征值求解的问题。但是对于奇异值以及奇异值分解的概念还是比较淡薄的。因此查阅了相关的文献将矩阵的特征值与奇异值以几何的形式展现出来。以便更好的理解其中的问题。文章主要参考的是Feature Column from the AMS这篇文献。虽然是英文的但是比较容易读懂。
在本科的时候我们都学习了矩阵特征值的概念,在书本上对特征值的定义是这样的:
设A是n阶方阵,如果数λ和n维非零列向量x使关系式 成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量。式 也可写成 。这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式 。
在代数上我们可以按照常规的方法来得到一个方阵的特征值,但是如何在几何直观上来正确理解特征值这样的问题呢?最主要的还是要从特征方程入手:
这里我们要求A必须为方阵。X是我们所得到的特征向量组成的矩阵, 是矩阵特征值组成的对角矩阵。更一般的表达式为:
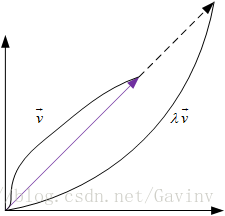
这里的 ,表示的是每一个特征值 ,所对应的特征向量。这样看起来就有了更加直观的认识,也就是说当我们对一个向量左乘一个系数变换的矩阵A,那么这个矩阵对向量产生的作用实际上就是对此向量在当前基下面沿着向量的方向进行 倍的拉伸。示意图如下:
从上图中可以很清晰的看出,对一个向量左乘一个系数方阵本质上就是沿着这个向量的方向对该向量进行拉伸,而拉伸的程度是由特征值的大小决定的。注意这里 , 的方向是一致的。只是长度不同而已。
矩阵奇异值实际上就是更加一般意义上的特征了,我们注意到对于矩阵特征值的求解中我们要求系数矩阵是一个方阵。但是在现实情况下我们求解的矩阵并非都是比较规则的方阵。而是更加一般意义的矩阵。对于奇异值的定义如下所示:
知道了矩阵奇异值的定义我们就知道了如何局算一个矩阵的奇异值,但是我们注意到奇异值是由特征值得到的,也就是说在求解奇异值的过程中仍然涉及到矩阵特征值的求解。要求特征值就必须构建一个方阵。这也就是矩阵奇异值分解的基础。
奇异值分解;
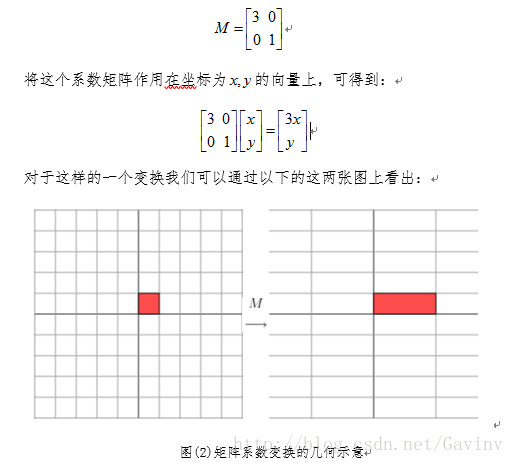
我们首先从几何意义上来理解矩阵的奇异值分解问题。如下所示我们首先给出一个对角矩阵M;
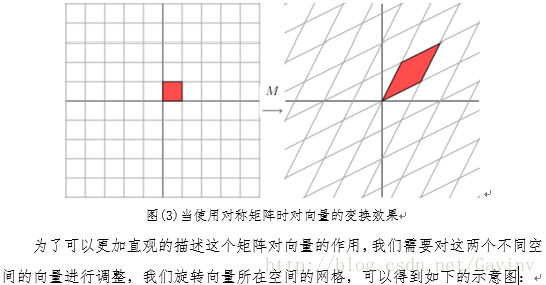
实际上上图可以看作是当系数矩阵的特征值为3,1时对向量变换之后的结果。可以看出原始的正交向量在通过对角矩阵的变换之后仍然是一个正交的向量。只是在x方向上产生了拉伸。那么对于对称矩阵是否有同样的效果呢?
当我们将系数矩阵设置为
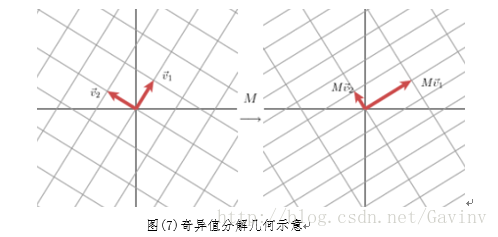
通过上述的说明实际上我们已经矩阵的奇异值分解有了一定的认识了,若果说矩阵的特征值是将向量在同一空间进行一定程度的拉伸而不改变方向的话,那么矩阵的奇异值分解实际上就是找到一组与原始的基相对应的正交基,来表示对原始向量的某一操作。这个过程我们可以通过具体表达式的形式来量化:
也就是说对于原始空间中的两个基向量,我们找到另一个空间中的一对正交基来表示,那么原始基向量表示的向量同样也可以由另一空间中的正交基表示出来。之所以要找到另一个相应的基来表示出原始的向量原因其实就在于在一个空间中需要M个数据可以表示的对象,在另一个空间只需要N个数据就可以表示出来。且N << M; 出于计算复杂度以及资源充分利用的考虑,我们更希望以更少的数据表示相同的内容。