SLAM总结(二)-数学基础之求导和线性方程求解
1.求导:高数中常见的是一个函数对一个自变量求导,属于标量对标量求导。在SLAM问题中,函数是目标函数(残差项,约束项),一般包含多个函数,用多维列向量表示;自变量是待估计的机体位姿和点的位姿,一般也是多维列向量,旋转可以用四元数或李代数表示。求导就是函数组成的矩阵/向量/标量中的每个元素对因变量组成的矩阵/向量/标量中的每个元素求导,高数中的求导知识都能用上。向量对向量、标量对矩阵和矩阵对标量求导的结果能用矩阵表示,但向量对矩阵求导就不好用矩阵表示了,发挥一下空间想象力它应该是一个三维矩阵,
a)下面列举结果能表示出来的几种矩阵求导,该方法适合位移这种没有冗余的变量求导:
1)标量a 对向量 θ 求导如下,

R为对称矩阵时,x
T
Rx对x求导的导数为2Rx;bx、x
T
b对x求导为b
2)β、θ分别是m×1和n×1向量,结果矩阵和分子方向一致,则定义
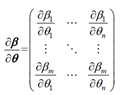
常见Aθ对θ的导数为A
3)a 是标量, M 是 m×n矩阵,则定义
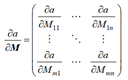
4)M 是 m×n 矩阵, a 是标量,则定义
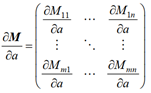
b)导数的一个用处是变量变多少能达到最优结果。旋转矩阵不仅求导比较复杂,而且旋转矩阵冗余太严重,即使求出每个变量的导数,用普通加法叠加,结果肯定不满足约束。优化和求导时,一般用四元数或李代数来表示,得到结果后再转换成矩阵形式表达。
1)用李代数表示,利用导数定义求导


2)利用扰动求导, 用李代数表示

3)利用扰动求导, 用四元数表示

4)数值方法求导,如1)利用导数定义求导,但Δx直接用接近于0数值表示,可代入导数定义直接通过计算机计算得到导数,简单直接,可用于验证上面3种方法解析结果的准确性
2.求解Ax=b,设A为mxn的矩阵,x为nx1维向量,b为mx1维向量。
求解前先介绍一个概念。对于mxn的矩阵A,A中最大的子行列式的阶数称为矩阵的秩,记为r(A)。
对于nxn的矩阵,r(A) =n <=> det(A)!=0 <=> A可逆 <=> A的行向量和列向量线性无关,其中det(A)表示A的行列式。
求解线性方程时只能对矩阵进行行变换,故这里令r(A)表示A的线性无关行向量的数量,也可以认为是有效的方程的数量,r(A)<=m,n为未知数数量。
求解思路是根据b和A矩阵的秩判断属于下列哪种情况,然后根据A矩阵形式选择合适的方法求解。在求解前可以先对A矩阵进行一些预处理,如消元(将矩阵转变成某块为0的方法,如schur、高斯消元)、plain和reording(调整变量排序,相当于调整A矩阵列的顺序),然后把A矩阵分解为上下三角或者正交矩阵后计算机才好求解,之后,上下三角可以通过“回代”求解,正交矩阵的转置即为逆,可直接求逆(先预处理,再分解,最后求解)。在计算过程中都不可以避免的用到矩阵乘法,矩阵乘法的计算复杂度是O(n
3
)。故计算复杂度一般是O(n
3
)或以上。一般在SLAM中无解和多解的情况是不存在的,且求解时矩阵的秩和矩阵的形式都是是已知的。之后SLAM分析中再具体分析。
a)b=0时为齐次方程
1)r(A)<n:方程有无穷多解,有n-r个线性无关解,求解时使用高斯消元法将A矩阵化为最简阶梯形矩阵,然后可求得通解
2)r(A)=n:方程有唯一0解
3)m>=r(A)>n:超定方程,可以求最小二乘解。SLAM常见的情况
对于齐次方程的情况,在SLAM一般使用SVD方法求解,多解和0解的情况一般不存在,下面主要讨论m>=r(A)>=n的情况。下面简单介绍一下SVD方法。
设 A 是秩为 r(r>0)的mxn实(复)矩阵,则存在m阶正交(酉)矩阵U 与 n 阶正交(酉)矩阵V ,使得A=UDV
T
,D为mxn对角矩阵,对角为A的奇异值(A
T
A、AA
T
的特征值开根号,为非负),习惯将D奇异值按降序排列,U、V的列也要跟着排序;U为AA
T
特征向量组成矩阵,V为A
T
A特征向量组成矩阵。
对于m>n的情况,D矩阵n+1到m行肯定都为0,那么U的n+1到m列与之相乘结果为0,故D矩阵取前n行,m取前n列即可。因而U变成mxn矩阵,D变成nxn矩阵。
求得U、D、V矩阵的计算复杂度是4m
2
n+8mn
2
+9n
3
次浮点运算,求V、D的计算复杂度是4mn
2
+8n
3
次浮点运算。在SLAM中一些问题只需求V、D且m>n,可以减少计算量。如解齐次方程的最小二乘解时只需求得V、D,故其计算复杂度大大降低,与较大的m成线性关系。
一般假设在m>=r(A)>=n和||x||=1条件下求||Ax||的最小二乘解,证明如下图所示,
参考链接

b)b!=0时为非齐次方程,设增广矩阵B=[A|b],可得r(B)>=r(A);当r(n)<=n时,r(B)=r(A)
先介绍一种在m>=n(m<n可以加全0行补齐)、秩未知的情况下使用SVD求解的方法,首先Ax=b可转换为min||Ax-b||求最小二乘解,求解方法如下图

1)r(A)=r(B)=r<n,方程有无穷多解,解为齐次方程解+特解
[1]SVD方法:与上图秩未知情况相似,相当于已知秩为r
2)r(A)!=r(B),则r(A)>n,方程无解,超定
[1]SVD方法:与上图相似,奇异值都为非0,则:x=DV
+
U
T
b,D
+
为伪逆,矩阵维度转置,非0对角取倒数,0保持不变
[2]两边同乘A
T
,r(A
T
A)=n(可逆),最小二乘解:x=(A
T
A)
-1
A
T
b
3)r(A)=r(B)=n,方程有唯一解。在SLAM中,非线性优化中最后求增量会变成这种形式,直接得到满秩的nxn矩阵。对于满秩的m>n的情况,两边同时乘AT便能得到nxn的形式
[1]直接求逆:x=A
-1
b。矩阵求逆的方法有如下, 除了公式法(伴随矩阵法)和特殊矩阵,其他矩阵求逆方法与求线性方程方法类似。公式法计算复杂度高,故除了特殊矩阵,没必要将线性求解问题转换成直接求逆。矩阵求逆也可以转换成求线程方程解的问题:b分别取单位阵的各个列向量,所得到的解向量x就是逆矩阵的各个列向量,拼成逆矩阵即可(
参考链接
)。
1、一般有公式法(伴随矩阵法):A-1=A*/det(A)。时间复杂度O(n^4)
2、初等矩阵变换法:与Guass消元相似。时间复杂度O(n^3)
3、LU方法:以下会详细介绍。时间复杂度O(n^3)
4、QR方法:数值稳定的,可以求解大型矩阵的逆。目前通用且最好的方法是QR分解,这个方法的复杂度是O(n^3)。
5、特殊矩阵可以采取特殊的方法,如上下三角矩阵、对角为矩阵块的矩阵求逆计算量较少。
[2]克拉默法则:计算复杂度需要(n+1)!(n-1)次乘法
x
i
=det(A
i
)/det(A),其中A
i
是A的第i列被b替换
[3]Guass消元法:一般地当维数很高时,公式法求逆和克拉默法则计算量很大,Guass消元法可以减少计算量,计算复杂度是n
3
/3+n
2
-n/3次乘除法,n
3
/3+n
2
-5n/6次加减法,时间复杂度O(n
3
)。该方法先根据矩阵行列变换将A矩阵化成最简阶梯形矩阵(上三角矩阵),然后再求解。为了避免绝对值小的数或0值主元带来得舍入误差或无法计算。第k步消元时通过行交换选取k-1步结果中绝对值最大得作为主元。这种方法称为叫Gauss列主元消去法。此方法中b跟着A一起边,相当于方程两边同时乘以同一个矩阵。
[4]矩阵三角(LU)分解方法:将A阵分解为两个三角阵相乘,即A=LU,然后再求解。分解的意思是只分解A矩阵,b不变。其实Guass消去法的变形,若Guass消元法的最简阶梯矩阵与U相等,则两边同乘L方程又变回原样。时间复杂度O(n
3
),总体来说和高斯消元法差不多,但是避免了高斯消元法的主元素为0的过程。
n 阶非奇异矩阵 A 可作三角分解的充要条件是A的各阶顺序主子式不为0。当L为单位下三角阵(对角线为1,上三角都为0)时为Doolittle分解,当U为单位上三角阵时为Crout分解。再将A=LDR,其中R=D
-1
U,L、R分别为单位上下三角矩阵,为LDR分解。三角分解不唯一,Doolittle分解、Crout分解、LDR分解唯一。对角线为1的好处是求解时不用除未知数的系数。
1、直接分解法:使用guass消元法直接求得LU,此时求出的就是Doolittle分解
2、Doolittle分解法:直接计算比较麻烦,使用A=LU来分解,假设条件就是L是单位下三角矩阵。A各元、素已知,逐行求U的元素,逐列求L的元素。
3、按列选主元的Doolittle分解:每步取列最大值,减小舍入误差
4、平方根法(Cholesky):A矩阵为实对称正定矩阵的情况(正定等价于A特征值都大于0),其三角化还可以简化。实对称矩阵正定的充要条件是各阶顺序主子式大于0。另外,实对称矩阵正定的充要条件是存在n阶非奇异下三角阵L使得A=LL
T
。L主对角元素为正数时,分解唯一。为了避免求L时的开方运算可使用改进的平方根法,A=LDLT,其中D为对角阵,L为单位下三角。G2O中的CHOLMOD和CSparse都是基于这一方法。
5、追赶法:用于A为三对角阵情况。
[5]QR分解方法:任何n阶实矩阵 A 可分解为正交(酉)矩阵Q和上三角矩阵 R (Right)的乘积,即A=QR,时间复杂度O(n
3
)。与之相似的方法有QL、LQ和RQ。分解完后解方程:Ax=QRx=b -> Rx=Q
-1
b=Q
T
b,R为上三角矩阵方程好求。Q为正交阵,逆等于转置。该方法具有收敛快、算法稳定等特点。QR分解方法,
参考链接
1、Gram-schmidt正交化方法:从A矩阵的n个列中构建互相正交的基,先选定第一列为第一个基,再利用A矩阵的列向量线性无关的性质使用正交化方法逐个构建完n个基。图片截自《线性系统理论数学基础》


2、Givens变换法:适合低维稀疏矩阵。Givens Rotations定义如下图所示,截自《数值分析与实验》,它是一个正交矩阵。可以使用它的转置构建Q,用它与A相乘构建R。

它与A矩阵相乘的一个用处就是将其中一个元素变为0,如下所示,但可能影响其他元素变成非零,这个范围比较小,只会影响A与Q非1行对应的两行元素。所以在使用时需要巧妙地使A的下三角为0,上三角非零不影响结果。该方法适合稀疏矩阵(0的元素可以忽略),对于稠密矩阵速度与其他两种方法相当。另外,Givens Rotations更容易并行化,因为每次只对两行元素进行操作,处理不同列是完全独立的。
3、Householder变换方法:该方法适合一般矩阵,如高维、稠密的。我在数值分析和《多视图几何》书中看到了两种不同的方法如下:
i:《数值分析与实验》中方法(如下图):将对称矩阵相似(特征值相同)约化为对称三对角矩阵,以及将-般的非对称矩阵相似约化为上Hessenberg(次对角线以下为0),然后使用Givens变换法更容易得到Q、R。该方法时一种迭代的方法。该方法还可以用来计算上Hessenberg矩阵以及对称三对角矩阵的全部特征值。

ii:《多视图几何》中方法(如下图):与i中表达方式有所不同,这里v为任意向量,但H
v
与i中H是一样的。

[6]PCG(预处理共轭梯度法,Preconditioned Conjugate Gradient):若A为对称正定矩阵。可以得到最优解x*
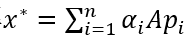
当n很大时,用直接法求解计算量大,可以使用迭代法。迭代法如下图所示,
参考链接
。该方法的收敛速度依赖初值x
0
的选取。

[7]schur消元:也称边缘化(Marginalization),即先边缘化一部分变量,求出剩下的变量,然后再求被边缘化中的变量。如《视觉SLAM十四讲》中列举的视觉的例子。后端优化时需要求解下式所示的线性方程。
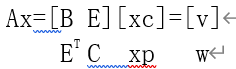
其中,xc维度为关键帧数量x6(pose自由度),xp维度为路标点数量x3(位移自由度),一般地,路标点数量远远大于关键帧数量,故xc维度远远大于xp维度。A矩阵的B、C块为对角块,E为稀疏矩阵。利用对角块求逆难度远小于一般矩阵求逆。可以按如下步骤求解:
i:方程两边同时乘矩阵边缘化xp(如下),可用之前解法解(B-EC
-1
E
T
)xc=v-EC
-1
w求得xc
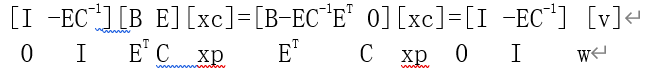
ii:xc已得到,C的逆已经求得,可以通过1)直接求逆的方法求得xp=C
-1
(w-E
T
xc)
以上主要计算量在求取C
-1
和解i中方程。当维度相同时,求解对角块矩阵的逆矩阵的计算量少于求解i中方程,若求C的逆的复杂度为O(n
3
),则分块求逆的复杂度为O(k
3
),k为对角块中维度最高的块的维度,故这里选择边缘化维度较高的xp求取维度较高的C矩阵的逆,而不是边缘化xc求取B矩阵的逆
[8]SVD方法:奇异值都为非0,则:x=DV
+
U
T
b,D
+
为伪逆,矩阵维度转置,非0对角取倒数,0保持不变