学习归并排序的一个重要原因是它是证明计算复杂度领域的一个重要结论的基础,而计算复杂度能够帮助我们理解排序自身固有的难易程度。计算复杂度在算法设计中扮演着非常重要的角色,而这个结论正是和排序算法的设计直接相关的。
研究复杂度的第一步是建立一个计算模型。一般来说,研究者会尽量寻找一个和问题相关的最简单的模型。对排序来说,我们的研究对象是基于比较的算法,它们对数组元素的操作方式是由主键的比较决定的。一个基于比较的算法在两次比较之间可能会进行任意规模的计算,但它只能通过主键之间的比较得到关于某个主键的信息。因此我们局限于实现了Comparable接口的对象,本章中的所有算法都属于这一类(注意,我们忽略了访问数组的开销)。
命题I。没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。
证明。首先,假设没有重复的主键,因为任何排序算法都必须能够处理这种情况。我们使用二叉树来表示所有的比较。树中结点要么是一片叶子
i0
i
1
i
2
.
.
.
i
N
−
1
i_0 i_1 i_2 … i_{N-1}
i
0
i
1
i
2
.
.
.
i
N
−
1
,表示排序完成且原输入的排序顺序是
a[
i
0
]
,
a
[
i
1
]
,
.
.
.
,
a
[
i
N
−
1
]
a[i_0],a[i_1],…,a[i_{N-1}]
a
[
i
0
]
,
a
[
i
1
]
,
.
.
.
,
a
[
i
N
−
1
]
,要么是一个内部结点i:j,表示a[i]和a[j]之间的一次比较操作,它是左子树表示a[i]小于a[j]时进行的其他比较,右子树表示a[i]大于a[j]时进行的其他比较。从根结点到叶子节点每一条路径对应着算法在建立叶子结点所示的顺序时进行的所有比较。例如,这是一棵N=3时的比较树。
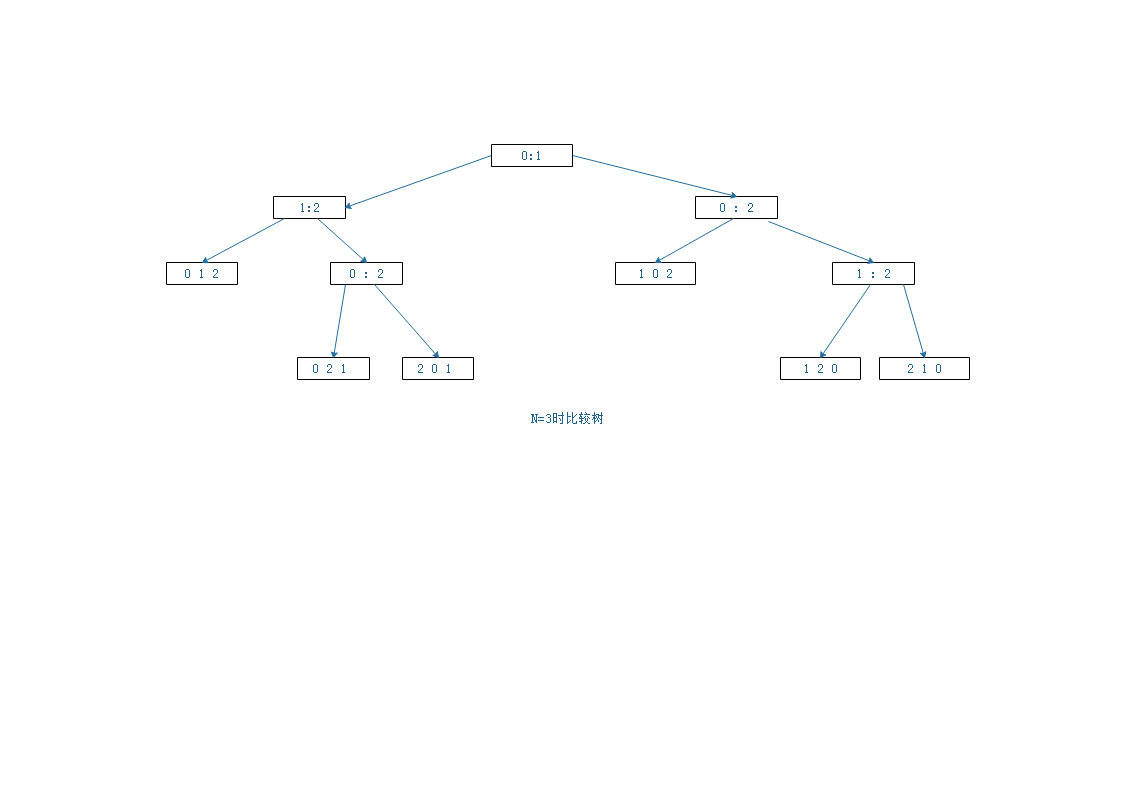
我们从来没有明确地构造这棵树-它只是用来描述算法中的比较的一个数学工具。
从比较树观察得到第一个重要的结论是这棵树应该至少有N!个叶子结点,因为N个不同的主键会有N!中不同的排列。
从根结点到叶子结点的一条路径上的内部结点的数量即是某种输入下算法进行比较的次数。我们感兴趣的是这种路径能有多长(也就是数的高度),因为这也就是算法比较次数最坏的情况。二叉树的一个基本的组合学性质就是高度为h的树最多只可能有
2h
2^h
2
h
个叶子结点,拥有
2h
2^h
2
h
个结点的树是完美平衡的,或称完全树。结合前两段的分析可知,任意基于比较的排序算法都对应着一棵高度为h的比较树,其中
N!
≤
叶
子
结
点
的
数
量
≤
2
h
N!\le 叶子结点的数量\le 2^h
N
!
≤
叶
子
结
点
的
数
量
≤
2
h
h的值就是最坏情况下的比较次数,因此对不等式的两边取对数即可得到任意算法的比较次数只是是lgN!。根据斯特灵公式对阶乘函数的近似可得lgN!~NlgN
这个结论告诉我们在设计排序算法的时候能够达到的最佳效果。
命题H表明归并排序在最坏情况下的比较差次数为~NlgN。这是其他排序算法复杂度的上限,也就是说更好的算法需要保证使用的比较次数更少。命题说明没有任何排序算法能够用少于~NlgN次比较将数组排序,这是其他排序算法的下限。也就是说,即使是最好的算法在最坏的情况下也至少需要这么多次的比较。
命题J。归并排序是一种渐进最优的基于比较排序的算法。
证明。更准确的说,这句话的意思是,归并排序在最坏的情况下的比较次数和任意基于比较的排序算法所需的最少的比较次数都是~NlgN。命题H和命题I都证明了这个结论。
需要强调的是,和计算模型一样,我们需要精确的定义最优算法。例如,我们可以严格地认为仅仅只需要lgN!次比较的算法才是最优的排序算法。我们不这么做的原因是,即使对于很大的N,这种算法和(比如说)归并排序之间的差异也并不明显。或者我们也可以放宽最优的定义,使之包含任意在最坏情况下的比较次数都在NlgN的某个常熟因子范围之内的排序算法。我们不这么做的原因是对于很大的N,这种算法和归并排序之间的差距还是很明显的。
计算复杂度的概念会让人觉得很抽象,单解决可计算问题内在困难的基础性研究则不管怎么说都是非常重要的。而且,在适用的情况下,关键在于计算复杂度会影响优秀软件的开发。首先准确的上界为软件工程师保证性能提供了空间。很多例子表明,平方级别排序的性能低于线性排序。其次,准确的下界可以为我们节省很多时间,避免因不可能的性能改变而投入资源。
但归并排序是最优性性不是结束,也不代表在实际应用中我们不会考虑其他的方法了,因为本节中的理论还是有许多局限的,例如:
- 归并排序的空间复杂度不是最优的
- 在实践中不一定会遇到最坏情况
- 除了比较,算法的其他操作(例如访问数组)也可能很重要
- 不进行比较也能将某些数据排序
QQ:806797785
仓库地址:https://gitee.com/gaogzhen/algorithm