博客

跳跃表Skip List的原理和实现(Java)

  • Post author:
  • Post category:java



【博文总目录>>>】

|

【代码下载>>>】

为什么要有跳跃表

我们在实际开发中经常会有在一堆数据中查找一个指定数据的需求，而常用的支持高效查找算法的实现方式有以下几种：

  1. 有序数组。这种方式的存储结构，优点是支持数据的随机访问，并且可以采用二分查找算法降低查找操作的复杂度。缺点同样很明显，插入和删除数据时，为了保持元素的有序性，需要进行大量的移动数据的操作。

  2. 二叉查找树。如果需要一个既支持高效的二分查找算法，又能快速的进行插入和删除操作的数据结构，那首先就是二叉查找树莫属了。缺点是在某些极端情况下，二叉查找树有可能变成一个线性链表。

  3. 平衡二叉树。二叉树表示不服，于是基于二叉查找树的优点，对其缺点进行改进，引入了平衡的概念。根据平衡算法的不同，具体实现有AVL树 ／

    B树（B-Tree） ／ B+树（B+Tree） ／ 红黑树 等等。但是平衡二叉树的实现多数比较复杂，较难理解。

  4. 跳跃表。同样支持对数据进行高效的查找，插入和删除数据操作也比较简单，最重要的就是实现比较平衡二叉树真是轻量几个数量级。缺点就是存在一定数据冗余。


PS: 网上看到很多文章说B树／B-树 ／ B+树 的，这是不正确的。没有B-树之说，英文资料中只存在B-Tree和B+Tree，然后翻译到中文，就把B-Tree翻译成了B-树，中间的“－”其实只是一个分隔号，并不是减号。

什么是跳跃表

跳跃表（SkipList）是一种可以替代平衡树的数据结构。跳跃表让已排序的数据分布在多层次的链表结构中，默认是将Key值升序排列的，以 0-1 的随机值决定一个数据是否能够攀升到高层次的链表中。它通过容许一定的数据冗余，达到 “以空间换时间” 的目的。

跳跃表的效率和AVL相媲美，查找／添加／插入／删除操作都能够在O（LogN）的复杂度内完成。

讲了那么多，下面就直接进入主题，详细的看一看跳跃表是怎么实现的。

跳跃表的实现

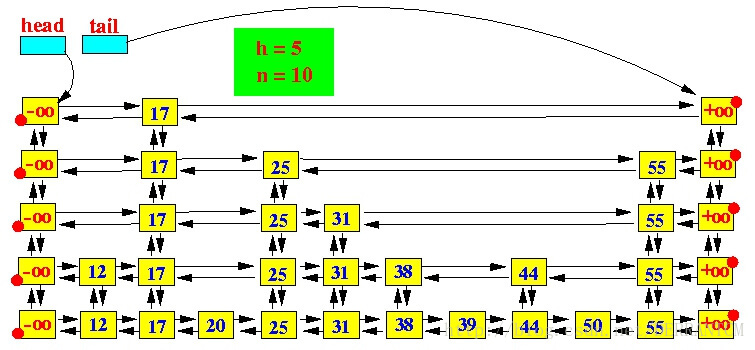
这里写图片描述

上面这张图就是一个跳跃表的实例，先说一下跳跃表的构造特征：

  • 一个跳跃表应该有若干个层（Level）链表组成；

  • 跳跃表中最底层的链表包含所有数据； 每一层链表中的数据都是有序的；

  • 如果一个元素X出现在第i层，那么编号比 i 小的层都包含元素X；

  • 第 i 层的元素通过一个指针指向下一层拥有相同值的元素；

  • 在每一层中，-∞ 和 +∞两个元素都出现(分别表示INT_MIN 和 INT_MAX)；

  • 头指针（head）指向最高一层的第一个元素；

首先，我们需要定义链表中节点的模型

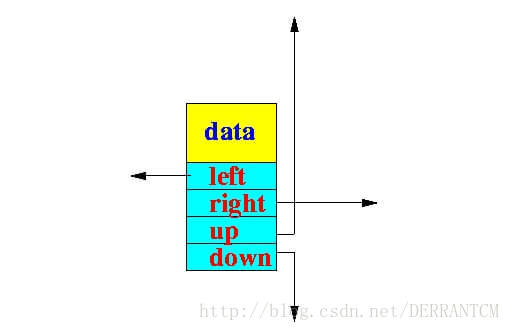
这里写图片描述

Java代码实现如下： 


    // data
    public String key;
    public Integer value;

    // links
    public SkipListEntry up;
    public SkipListEntry down;
    public SkipListEntry left;
    public SkipListEntry right;

    // special
    public static final String negInf = "-oo";
    public static final String posInf = "+oo";

    // constructor
    public SkipListEntry(String key, Integer value) {
        this.key = key;
        this.value = value;
    }

    // methods...
}

可以看到节点模型主要分为2个部分。

data部分包含具体的存储数据，这里为了不引入其他杂乱的问题，使用String作为key的类型，Integer作为value的类型。

links部分包含4个指针，分别是up，down，left，right，单从名字上就能够明白它们的作用。

最后一个需要解释的是，2个special的字符串变量，它们是用来处理一些特殊节点的初始化的，从上面的图中可以看到，跳跃表每一层链表中都有那么2个节点。具体的初始化方法如下： 

SkipListEntry x = new SkipListEntry(SkipListEntry.negInf, null);
SkipListEntry y = new SkipListEntry(SkipListEntry.posInf, null);

接下来，我们回到跳跃表本身的模型

public class SkipList {

    public SkipListEntry head;  // First element of the top level
    public SkipListEntry tail;  // Last element of the top level

    public int n;       // number of entries in the Skip List
    public int h;       // Height

    public Random r;    // Coin toss
}


Note: Random类的实例对象r用来决定新添加的节点是否能够向更高一层的链表攀升。

初始化一个跳跃表的实例

构造函数将初始化一个空的跳跃表看起来像下面这样：

这里写图片描述

构造函数的Java代码： 

// constructor
public SkipList() {
    SkipListEntry p1, p2;

    // 创建一个 -oo 和一个 +oo 对象
    p1 = new SkipListEntry(SkipListEntry.negInf, null);
    p2 = new SkipListEntry(SkipListEntry.posInf, null);

    // 将 -oo 和 +oo 相互连接
    p1.right = p2;
    p2.left = p1;

    // 给 head 和 tail 初始化
    head = p1;
    tail = p2;

    n = 0;
    h = 0;
    r = new Random();
}

实现Map的基本操作

Map的基本操作：

  • get(String key) ： 根据key值查找某个元素

  • put(String key, Integer value) ：插入一个新的元素，元素已存在时为修改操作

  • remove(String key)： 根据key值删除某个元素

虽然看似是3个不同的操作，但是究其本质，要实现这3个操作，都得先找到某个元素 或是 定位到一个元素，好在下一个位子插入新元素。那么，我们就先把这个findEntry的方法实现吧。

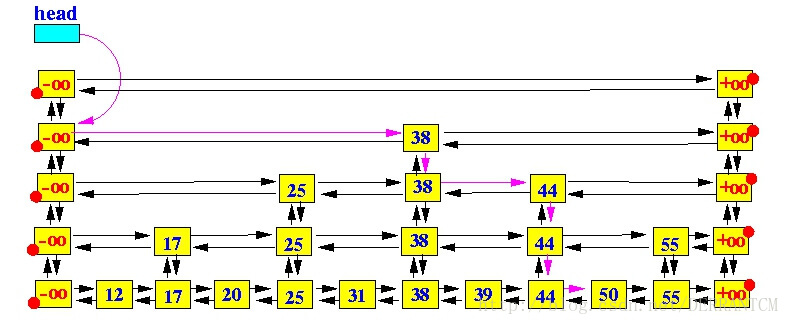
这里写图片描述

上面的图示使用紫色的箭头画出了在一个SkipList中查找key值50的过程。简述如下：

  1. 从head出发，因为head指向最顶层（top level）链表的开始节点，相当于从顶层开始查找；

  2. 移动到当前节点的右指针（right）指向的节点，直到右节点的key值大于要查找的key值时停止；

  3. 如果还有更低层次的链表，则移动到当前节点的下一层节点（down），如果已经处于最底层，则退出；

  4. 重复第2步 和 第3步，直到查找到key值所在的节点，或者不存在而退出查找；

Java代码实现如下： 

private SkipListEntry findEntry(String key) {

    SkipListEntry p;

    // 从head头节点开始查找
    p = head;

    while(true) {
        // 从左向右查找，直到右节点的key值大于要查找的key值
        while(p.right.key != SkipListEntry.posInf
                && p.right.key.compareTo(key) <= 0) {
            p = p.right;
        }

        // 如果有更低层的节点，则向低层移动
        if(p.down != null) {
            p = p.down;
        } else {
            break;
        }
    }

    // 返回p，！注意这里p的key值是小于等于传入key的值的（p.key <= key）
    return p;
}

注意以下几点：

  1. 如果传入的key值在跳跃表中存在，则findEntry返回该对象的底层节点；

  2. 如果传入的key值在跳跃表中不存在，则findEntry返回跳跃表中key值小于key，并且key值相差最小的底层节点；

示例，在跳跃表中查找key＝42的元素节点，将返回key＝39的节点。如下图所示：

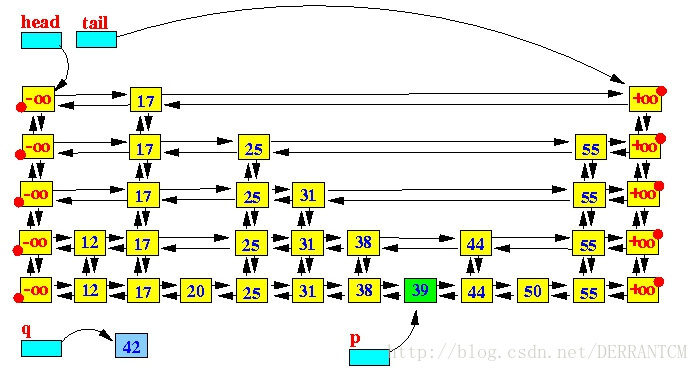
这里写图片描述

基于findEntry方法，我们就能很容易的实现前面所说的一些操作了。

实现get方法

public Integer get(String key) {

    SkipListEntry p;

    p = findEntry(key);

    if(p.key.equals(key)) {
        return p.value;
    } else {
        return null;
    }
}

实现put方法

put方法有一些需要注意的步骤：

  1. 如果put的key值在跳跃表中存在，则进行修改操作；

  2. 如果put的key值在跳跃表中不存在，则需要进行新增节点的操作，并且需要由random随机数决定新加入的节点的高度（最大level）；

  3. 当新添加的节点高度达到跳跃表的最大level，需要添加一个空白层（除了-oo和+oo没有别的节点）

下面我们一步一步的通过图示看一下插入节点的过程：

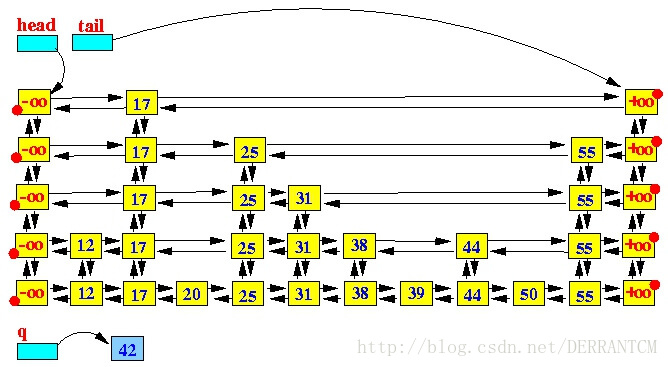
这里写图片描述


第一步，查找适合插入的位子

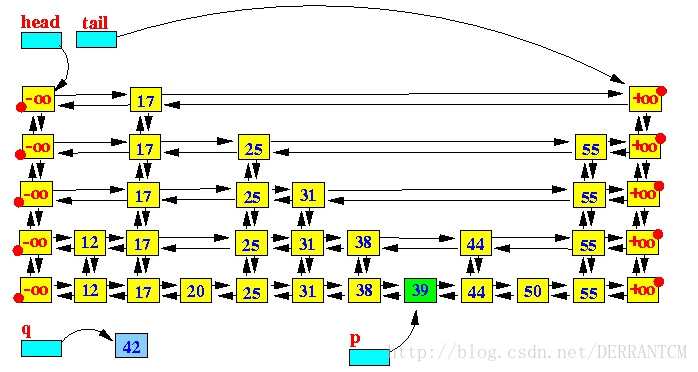
这里写图片描述


第二步，在查找到的p节点后面插入新增的节点q

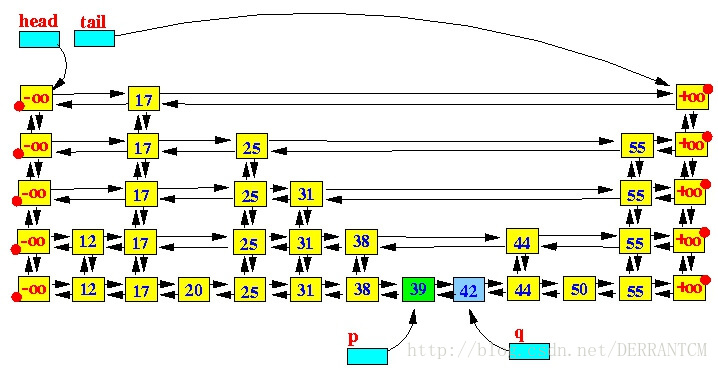
这里写图片描述


第三步，重复下面的操作，使用随机数决定新增节点的高度

从p节点开始，向左移动，直到找到含有更高level节点的节点；

将p指针向上移动一个level；

创建一个和q节点data一样的节点，插入位子在跳跃表中p的右方和q的上方；

直到随机数不满足向上攀升的条件为止；

图示如下：

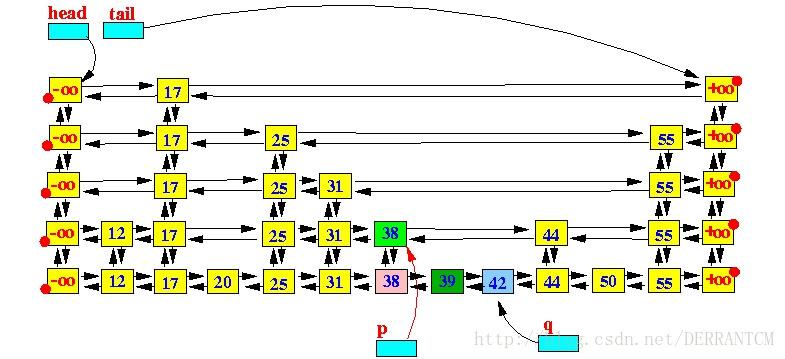
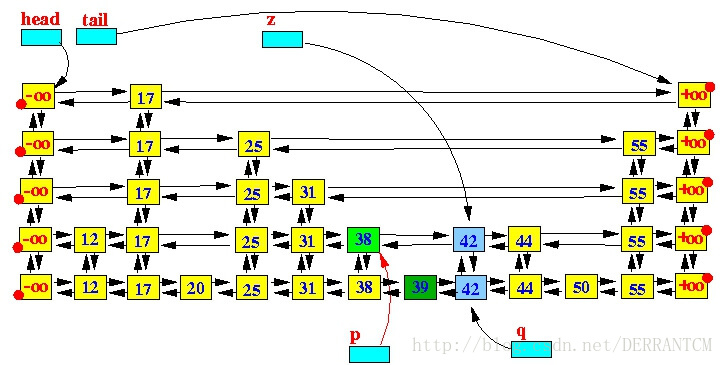
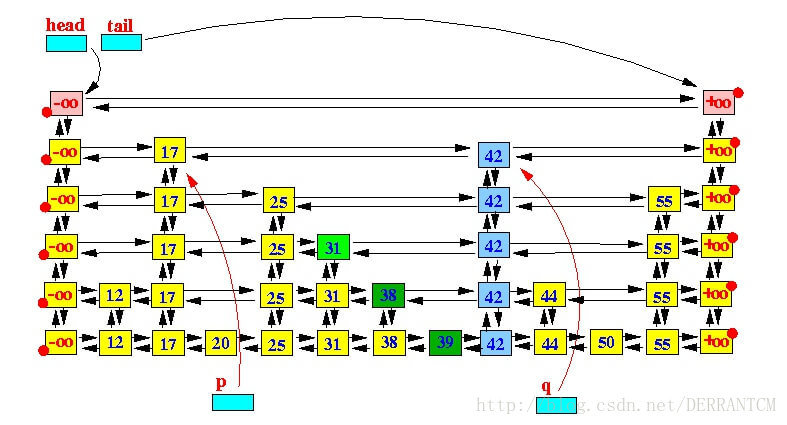
这里写图片描述

这里写图片描述

这里写图片描述

只要随机数满足条件，key＝42的节点就会一直向上攀升，直到它的level等于跳跃表的高度（height）。这个时候我们需要在跳跃表的最顶层添加一个空白层，同时跳跃表的height＋1，以满足下一次新增节点的操作。

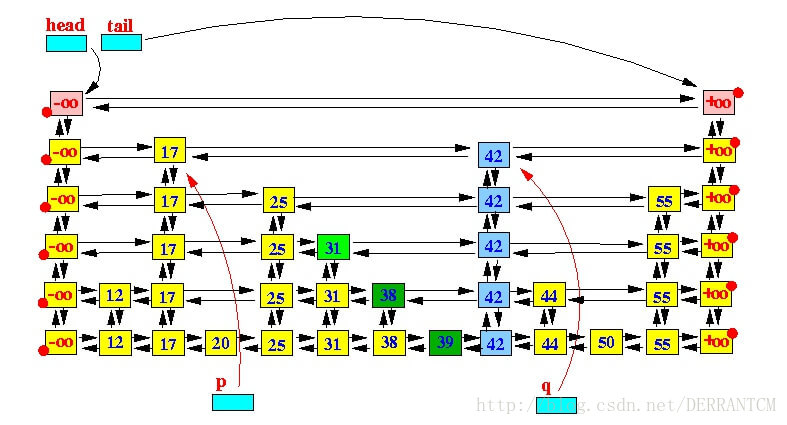
这里写图片描述

Java代码实现如下： 

public Integer put(String key, Integer value) {

    SkipListEntry p, q;
    int i = 0;

    // 查找适合插入的位子
    p = findEntry(key);

    // 如果跳跃表中存在含有key值的节点，则进行value的修改操作即可完成
    if(p.key.equals(key)) {
        Integer oldValue = p.value;
        p.value = value;
        return oldValue;
    }

    // 如果跳跃表中不存在含有key值的节点，则进行新增操作
    q = new SkipListEntry(key, value);
    q.left = p;
    q.right = p.right;
    p.right.left = q;
    p.right = q;

    // 再使用随机数决定是否要向更高level攀升
    while(r.nextDouble() < 0.5) {

        // 如果新元素的级别已经达到跳跃表的最大高度，则新建空白层
        if(i >= h) {
            addEmptyLevel();
        }

        // 从p向左扫描含有高层节点的节点
        while(p.up == null) {
            p = p.left;
        }
        p = p.up;

        // 新增和q指针指向的节点含有相同key值的节点对象
        // 这里需要注意的是除底层节点之外的节点对象是不需要value值的
        SkipListEntry z = new SkipListEntry(key, null);

        z.left = p;
        z.right = p.right;
        p.right.left = z;
        p.right = z;

        z.down = q;
        q.up = z;

        q = z;
        i = i + 1;
    }

    n = n + 1;

    // 返回null，没有旧节点的value值
    return null;
}

private void addEmptyLevel() {

    SkipListEntry p1, p2;

    p1 = new SkipListEntry(SkipListEntry.negInf, null);
    p2 = new SkipListEntry(SkipListEntry.posInf, null);

    p1.right = p2;
    p1.down = head;

    p2.left = p1;
    p2.down = tail;

    head.up = p1;
    tail.up = p2;

    head = p1;
    tail = p2;

    h = h + 1;
}

实现remove方法

删除节点的操作相对put就比较简单了，首先查找到包含key值的节点，将节点从链表中移除，接着如果有更高level的节点，则repeat这个操作即可。

Java代码实现如下： 

public Integer remove(String key) {

    SkipListEntry p, q;

    p = findEntry(key);

    if(!p.key.equals(key)) {
        return null;
    }

    Integer oldValue = p.value;
    while(p != null) {
        q = p.up;
        p.left.right = p.right;
        p.right.left = p.left;
        p = q;
    }

    return oldValue;
}

跳跃表的原理和实现到这里就结束了。

还有需要说明的一点是：跳跃表每次运行的结果是不一样的，这就是为什么说跳跃表是属于随机化数据结构。（Random的存在导致的）

跳跃表在Java中的应用

  • ConcurrentSkipListMap：在功能上对应HashTable、HashMap、TreeMap；

  • ConcurrentSkipListSet ： 在功能上对应HashSet；

确切的说，SkipList更像Java中的TreeMap，TreeMap基于红黑树（一种自平衡二叉查找树）实现的，时间复杂度平均能达到O(log n)。

HashMap是基于散列表实现的，查找时间复杂度平均能达

到O(1)。ConcurrentSkipListMap是基于跳跃表实现的，查找时间复杂度平均能达到O(log n)。

ConcurrentSkipListMap具有SkipList的性质 ，并且适用于大规模数据的并发访问。多个线程可以安全地并发执行插入、移除、更新和访问操作。与其他有锁机制的数据结构在巨大的压力下相比有优势。

TreeMap插入数据时平衡树采用严格的旋转操作（比如平衡二叉树有左旋右旋）来保证平衡，因此SkipList比较容易实现，而且相比平衡树有着较高的运行效率。

转载自：

http://hacking.love/


版权声明：本文为DERRANTCM原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
Tags: