博客

红黑树

性质

1. 红黑树定义

• 每个节点必须为红色或者黑色
• 根为黑色
• 树中的null叶子为黑
• 若节点为红，则其两个孩子必为黑
• 每个节点到其后代叶子的所有路径含有同样多的黑节点

2. 黑高定义
   
   节点x的黑高bh(x)是该节点到它的任何后代叶子路径上黑节点数(不包括X本身)
   
   引理

   一颗n个内点的红黑树的高度至多是2log(n+1)

插入

• setp1将z节点按BST树规则插入红黑树中
• step2将z涂红
• setp3调整使其满足红黑树性质

调整分析

• 若z为根，将其涂黑
• 若z为非根，则p[z] (双亲节点)存在

• 若p[z]为黑，无需调整
• 若p[z]为红，违反性质4需要调整，一共六种情况
  
  case1:z的叔叔y是红色
  
  

case2:当z的叔叔y是黑色，且z是双亲p[z]的右孩子(LR)

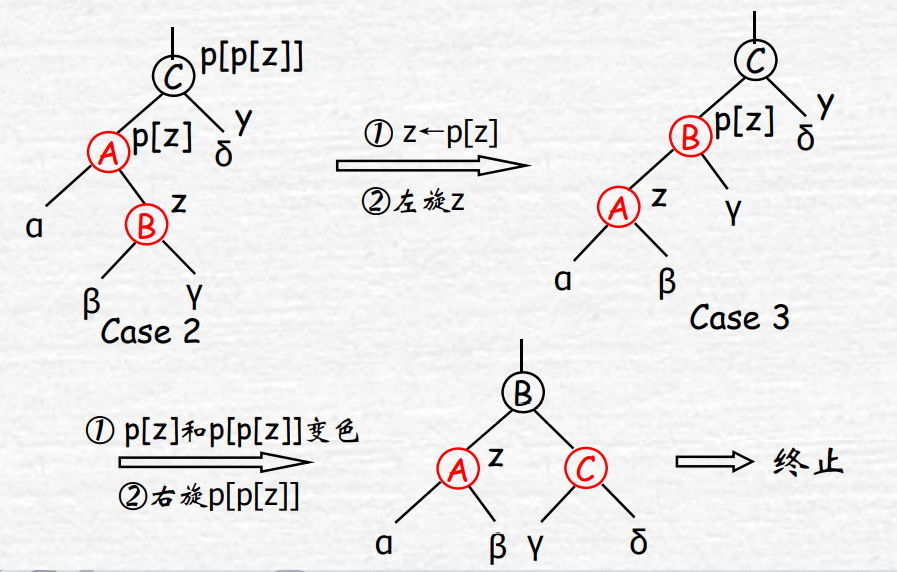
case3:当z的叔叔y是黑色，且z是双亲p[z]的左孩子(LL)

3:当z的叔叔y是黑色，且z是双亲p[z]的左孩子(LL)

case4-case6为z为p[z]的右孩子，情况类似