RNN（recurrent neural network）（二）——动手实现一个RNN

RNN系列博客：

RNN（recurrent neural network）（一）——基础知识
RNN（recurrent neural network）（二）——动手实现一个RNN

经过上篇博客《

RNN（recurrent neural network）（一）——基础知识

》的介绍，大家应该对RNN的结构以及如何运行的有个比较清晰地认识了，这一篇博客再来挑战更难一点的任务——自己动手撸一个RNN，相信自己动手写完后，会对RNN有一个更深的了解。这篇博客主要从两个部分介绍，首先对RNN的bp做一个推导，其次就是用python编程实现RNN。

注：代码部分几乎完全使用ng deep-learning课的作业代码。

一、RNN的前向传播

首先还是直接放上ng在《sequence model》课程里的图：

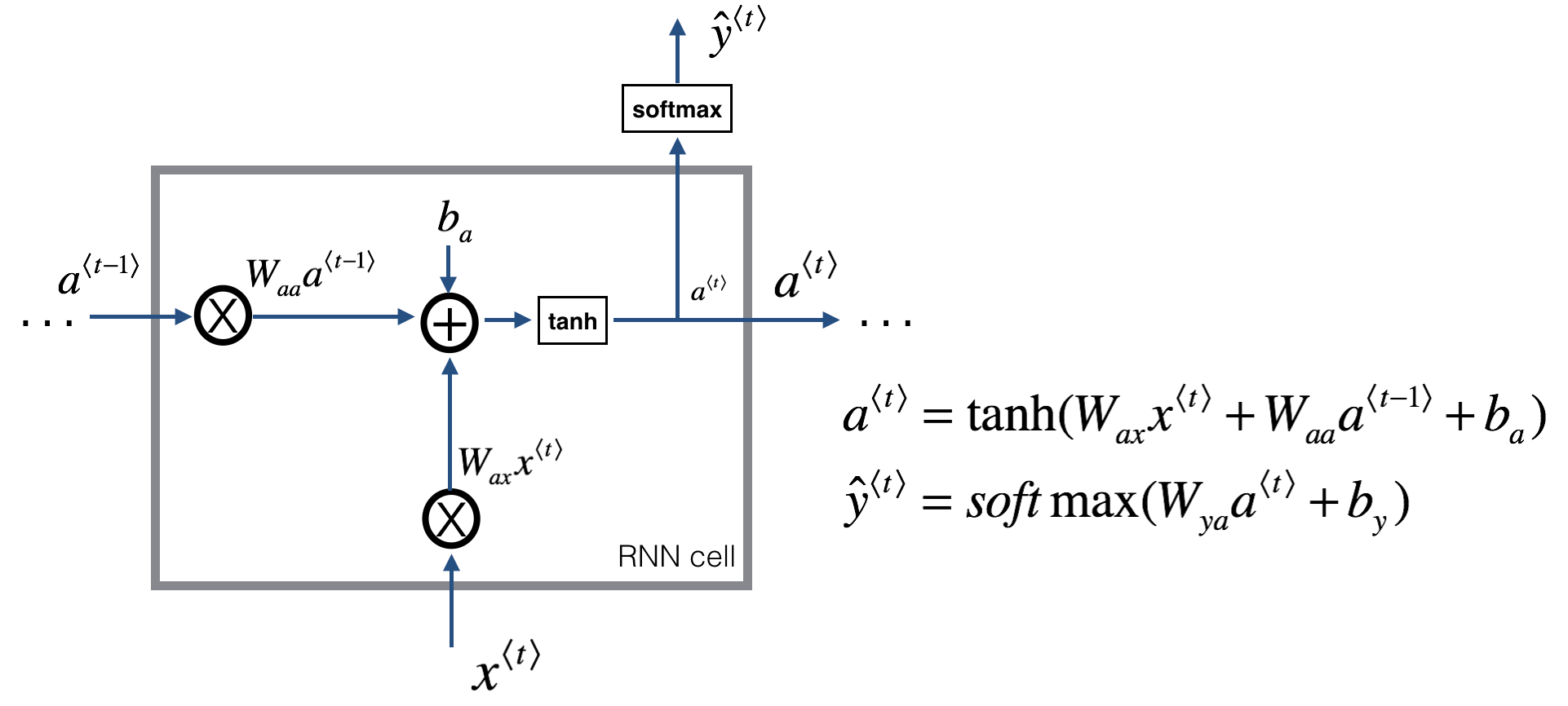
这是单个cell的，那么整个forward propagation的示意图为（图来自ng《sequence model》课）：

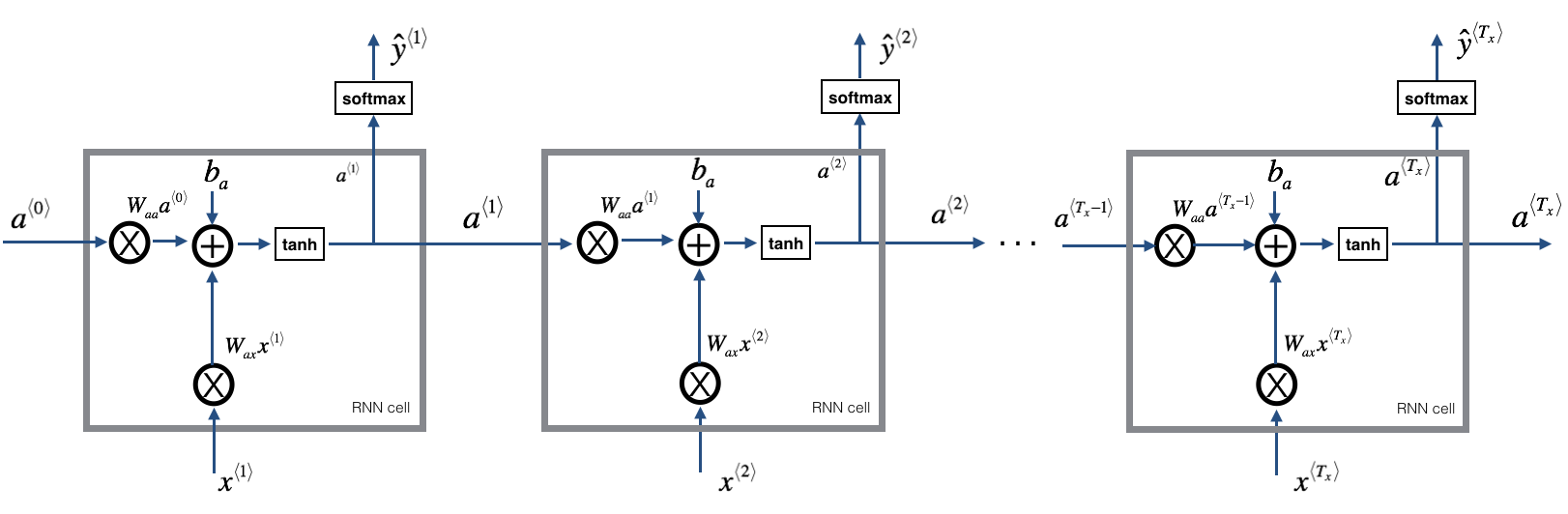
图二、RNN结构

因此，前向传播的公式为：

(

−

)

a^{<t>} = tanh(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a)

$a^{< t >} = t a n h (W_{a x} x^{< t >} + W_{a a} a^{< t - 1 >} + b_{a})$

(

)

\widehat{y}^{<t>} = softmax(W_{ya}a^{<t>} + b_y)

$y^{< t >} = s o f t m a x (W_{y a} a^{< t >} + b_{y})$

二、损失函数（Loss function）

机器学习任务，首先得有个目标，自然就是loss函数了，RNN的loss函数使用交叉熵（cross entropy），接下来我对RNN的loss函数可能会讲的比较细，主要是为了让大家能够了解清楚。我们把应用场景选定为ng的课后作业——生成恐龙名字，说白了就是生个一个单词，具体细节就是在给定前k个字符的情况下，生成最合理的第k+1个字符，首先假设训练集有

n

$n$

个样本（sequence），一个样本就是一个单词（恐龙名字），也可以理解为一个sequence，因为字符之间存在顺序关系。对于某一个sequence，RNN的结构就如图二所示，对于单个cell而言，loss函数为：

(

)

(

)

(

)

∑

∣

−

(

)

(

)

L^{(i)<t>} (\widehat{y}^{(i)<t>}, y^{(i)<t>}) = \sum_{k=1}^{|C|}-y_k^{(i)<t>}log\widehat{y}_k^{(i)<t>}

$L^{(i) < t >} (y^{(i) < t >}, y^{(i) < t >}) = k = 1 \sum ∣ C ∣ - y_{k}^{(i) < t >} l o g y_{k}^{(i) < t >}$

这里，

C

$C$

是类别，一般就是词表的大小。

y^{<t>}

$y^{< t >}$

是真实值，一般是个one-hot向量，大小等于词表的大小，

\widehat{y}^{<t>}

$y^{< t >}$

也是个向量，是softmax层输出的概率分布，大小也是词表的大小，两个向量是点乘，即对应元素相乘，但因为

y^{<t>}

$y^{< t >}$

是个one-hot向量，所以只有是1个那个元素起了作用，其他都是0。

因此，对于一个sequence来说，Loss函数为：

(

)

(

)

∑

(

)

(

)

(

)

−

∑

∣

(

)

(

)

\begin{array}{lcl} L (\widehat{y}^{(i)}, y^{(i)}) & = & \sum_{t=1}^{T_x}L^{(i)<t>} (\widehat{y}^{(i)<t>}, y^{(i)<t>})\\\\ & = & -\sum_{t=1}^{T_x}\sum_{k=1}^{|C|}y_k^{(i)<t>}log\widehat{y}_k^{(i)<t>} \end{array}

$L (y^{(i)}, y^{(i)}) = = \sum_{t = 1}^{T_{x}} L^{(i) < t >} (y^{(i) < t >}, y^{(i) < t >}) - \sum_{t = 1}^{T_{x}} \sum_{k = 1}^{∣ C ∣} y_{k}^{(i) < t >} l o g y_{k}^{(i) < t >}$

这里

T_x

$T_{x}$

是一个sequence的长度，那么在整个训练集上的Loss函数为：

(

)

∑

(

)

(

)

(

)

−

∑

∣

(

)

(

)

\begin{array}{lcl} L (\widehat{y}, y) & = & \frac{1}{n}\sum_{i=1}^{n}\sum_{t=1}^{T_x}L^{(i)<t>} (\widehat{y}^{(i)<t>}, y^{(i)<t>})\\\\ & = & -\frac{1}{n}\sum_{i=1}^{n}\sum_{t=1}^{T_x}\sum_{k=1}^{|C|}y_k^{(i)<t>}log\widehat{y}_k^{(i)<t>} \end{array}

$L (y, y) = = \frac{1}{n} \sum_{i = 1}^{n} \sum_{t = 1}^{T_{x}} L^{(i) < t >} (y^{(i) < t >}, y^{(i) < t >}) - \frac{1}{n} \sum_{i = 1}^{n} \sum_{t = 1}^{T_{x}} \sum_{k = 1}^{∣ C ∣} y_{k}^{(i) < t >} l o g y_{k}^{(i) < t >}$

之所以要求个均值，是为了更加准确的刻画网络在数据上的拟合程度，方便loss之间的比较，比如一个数据集有10w条样本，而另一个有1000条，如果不求均值，那么即使在10w条样本上的那个网络性能更好，也有可能loss比在1000条上的大。

三、后向传播（back-propagation through time,BPTT）

实际上，RNN中bp应该叫back-propagation through time,BPTT（通过时间反向传播），其实还是和bp一样，只是名字更加生动形象。我们的目标是求

W_{ax}

$W_{a x}$

、

W_{aa}

$W_{a a}$

、

W_{ya}

$W_{y a}$

、

b_y

$b_{y}$

、

b_a

$b_{a}$

的梯度（导数），还是要再放一下这个图，因为没办法，太需要了。

在求上面几个参数的导数之前，先把

(

)

tanh(x)

$t a n h (x)$

的导数求了，因为后面很多地方都要用到。

(

)

tanh(x)

$t a n h (x)$

的公式为：

(

)

−

tanh(x) = \frac{1 – e^{-2x}}{1 + e^{-2x}}

$t a n h (x) = \frac{1 - e ^{- 2 x}}{1 + e ^{- 2 x}}$

因此，导数为：

(

)

′

−

⋅

(

−

)

(

−

)

−

(

−

)

⋅

−

⋅

(

−

)

(

−

)

−

(

−

)

−

(

−

)

−

(

)

\begin{aligned} {tanh(x)}' &= \frac{- e^{-2x}\cdot(-2)(1 + e^{-2x})^{2} – (1 – e^{-2x})\cdot e^{-2x}\cdot(-2)}{(1 + e^{-2x})^{2}}\\ &= \frac{4e^{-2x}}{(1 + e^{-2x})^{2}}\\\\ &= 1- (\frac{1 – e^{-2x}}{1 + e^{-2x}})^2\\\\ &=1 – tanh^2(x) \end{aligned}

$t a n h (x)^{'} = \frac{- e ^{- 2 x} \cdot ( - 2 ) ( 1 + e ^{- 2 x} ) ^{2} - ( 1 - e ^{- 2 x} ) \cdot e ^{- 2 x} \cdot ( - 2 )}{( 1 + e ^{- 2 x} ) ^{2}} = \frac{4 e ^{- 2 x}}{( 1 + e ^{- 2 x} ) ^{2}} = 1 - (\frac{1 - e ^{- 2 x}}{1 + e ^{- 2 x}})^{2} = 1 - t a n h^{2} (x)$

根据求导时的链式法则：

∂

⋅

∂

⋅

′

(

−

)

⋅

∂

⋅

(

−

(

−

)

⋅

)

\begin{aligned} \frac{\partial L}{\partial W_{ax}} &= \frac{\partial L}{\partial a^{<t>}}\cdot \frac{\partial a^{<t>}}{\partial W_{ax}}\\\\ &=\frac{\partial L}{\partial a^{<t>}}\cdot {tanh}'(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a)\cdot x^{<t>}\\\\ &=\frac{\partial L}{\partial a^{<t>}}\cdot (1 – tanh^2(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a)\cdot x^{<t>}) \end{aligned}

$\frac{\partial L}{\partial W _{a x}} = \frac{\partial L}{\partial a ^{< t >}} \cdot \frac{\partial a ^{< t >}}{\partial W _{a x}} = \frac{\partial L}{\partial a ^{< t >}} \cdot t a n h^{'} (W_{a x} x^{< t >} + W_{a a} a^{< t - 1 >} + b_{a}) \cdot x^{< t >} = \frac{\partial L}{\partial a ^{< t >}} \cdot (1 - t a n h^{2} (W_{a x} x^{< t >} + W_{a a} a^{< t - 1 >} + b_{a}) \cdot x^{< t >})$

∂

⋅

∂

⋅

′

(

−

)

⋅

−

∂

⋅

(

−

(

−

)

⋅

−

)

\begin{aligned} \frac{\partial L}{\partial W_{aa}} &= \frac{\partial L}{\partial a^{<t>}}\cdot \frac{\partial a^{<t>}}{\partial W_{aa}}\\\\ &=\frac{\partial L}{\partial a^{<t>}}\cdot {tanh}'(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a)\cdot a^{<t-1>}\\\\ &=\frac{\partial L}{\partial a^{<t>}}\cdot (1 – tanh^2(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a)\cdot a^{<t-1>}) \end{aligned}

$\frac{\partial L}{\partial W _{a a}} = \frac{\partial L}{\partial a ^{< t >}} \cdot \frac{\partial a ^{< t >}}{\partial W _{a a}} = \frac{\partial L}{\partial a ^{< t >}} \cdot t a n h^{'} (W_{a x} x^{< t >} + W_{a a} a^{< t - 1 >} + b_{a}) \cdot a^{< t - 1 >} = \frac{\partial L}{\partial a ^{< t >}} \cdot (1 - t a n h^{2} (W_{a x} x^{< t >} + W_{a a} a^{< t - 1 >} + b_{a}) \cdot a^{< t - 1 >})$

∂

⋅

∂

⋅

′

(

−

)

∂

⋅

(

−

(

−

)

\begin{aligned} \frac{\partial L}{\partial b_{a}} &= \frac{\partial L}{\partial a^{<t>}}\cdot \frac{\partial a^{<t>}}{\partial b_{a}}\\\\ &=\frac{\partial L}{\partial a^{<t>}}\cdot {tanh}'(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a)\\\\ &=\frac{\partial L}{\partial a^{<t>}}\cdot (1 – tanh^2(W_{ax}x^{<t>} + W_{aa}a^{<t-1>} + b_a)) \end{aligned}

$\frac{\partial L}{\partial b _{a}} = \frac{\partial L}{\partial a ^{< t >}} \cdot \frac{\partial a ^{< t >}}{\partial b _{a}} = \frac{\partial L}{\partial a ^{< t >}} \cdot t a n h^{'} (W_{a x} x^{< t >} + W_{a a} a^{< t - 1 >} + b_{a}) = \frac{\partial L}{\partial a ^{< t >}} \cdot (1 - t a n h^{2} (W_{a x} x^{< t >} + W_{a a} a^{< t - 1 >} + b_{a}))$

接下来是求

W_{ya}

$W_{y a}$

和

b_y

$b_{y}$

的梯度，还有要求

∂

\frac{\partial L}{\partial a^{<t>}}

$\frac{\partial L}{\partial a ^{< t >}}$

，这都涉及到softmax求导，softmax的求导会稍微复杂一点。在RNN cell中预测值的输出为：

(

)

\widehat{y}^{<t>} = softmax(W_{ya}a^{<t>} + b_y)

$y^{< t >} = s o f t m a x (W_{y a} a^{< t >} + b_{y})$

为了求导方便，我们先令：

Z^{<t>}=W_{ya}a^{<t>} + b_y

$Z^{< t >} = W_{y a} a^{< t >} + b_{y}$

，那么：

(

)

∑

\begin{aligned} \widehat{y}^{<t>}_k &= softmax(Z^{<t>}_k)\\ &= \frac{e^{Z^{<t>}_k}}{\sum_{l=1}^Ce^{Z^{<t>}_l}} \end{aligned}

$y_{k}^{< t >} = s o f t m a x (Z_{k}^{< t >}) = \frac{e ^{Z_{k}^{< t >}}}{\sum _{l = 1}^{C} e ^{Z_{l}^{< t >}}}$

其中，

k

$k$

表示预测样本属于第

k

$k$

类，

C

$C$

表示类别数目，比如常见的二分类，那么

C=2

$C = 2$

，在自然语言处理序列任务中，C一般等于词表大小。

对softmax求导，有一点要考虑的就是，因为经过softmax的输出有：[

^

1

<

t

>

\widehat{y}^{<t>}_1

$y_{1}^{< t >}$

，

^

2

<

t

>

\widehat{y}^{<t>}_2

$y_{2}^{< t >}$

，…，

^

C

<

t

>

\widehat{y}^{<t>}_C

$y_{C}^{< t >}$

] ，假如求

L

∂

Z

j

<

t

>

\frac{\partial L}{\partial {Z}^{<t>}_j}

$\frac{\partial L}{\partial Z _{j}^{< t >}}$

，其实从

^

1

<

t

>

\widehat{y}^{<t>}_1

$y_{1}^{< t >}$

到

^

C

<

t

>

\widehat{y}^{<t>}_C

$y_{C}^{< t >}$

都包含

j

<

t

>

{Z}^{<t>}_j

$Z_{j}^{< t >}$

（

^

j

<

t

>

\widehat{y}^{<t>}_j

$y_{j}^{< t >}$

分子分母都包含，其它的

C

$C$

–

1

$1$

项（

^

k

<

t

>

，

k

≠

j

\widehat{y}^{<t>}_k，k\neq j

$y_{k}^{< t >} ， k ̸ = j$

）只有分母包含），所以这时候就要分上面两种情况来分开求导。

因此，对于某一个cell（就当做是最后一个cell吧，这样理解可能更容易懂），我们把loss函数拆写成两部分：

(

)

∑

(

)

(

)

(

)

−

∑

∣

(

)

(

)

−

∑

[

∑

≠

∣

(

)

(

)

(

)

(

)

]

\begin{array}{lcl} L (\widehat{y}^{<t>}, y^{<t>}) & = & \frac{1}{n}\sum_{i=1}^{n}L^{(i)<t>} (\widehat{y}^{(i)<t>}, y^{(i)<t>})\\\\ & = & -\frac{1}{n}\sum_{i=1}^{n}\sum_{k=1}^{|C|}y_k^{(i)<t>}log\widehat{y}_k^{(i)<t>}\\\\ &=& -\frac{1}{n}\sum_{i=1}^{n}[\sum_{k=1,k\neq j}^{|C|}y_k^{(i)<t>}log\widehat{y}_k^{(i)<t>} + y_j^{(i)<t>}log\widehat{y}_j^{(i)<t>}] \end{array}

$L (y^{< t >}, y^{< t >}) = = = \frac{1}{n} \sum_{i = 1}^{n} L^{(i) < t >} (y^{(i) < t >}, y^{(i) < t >}) - \frac{1}{n} \sum_{i = 1}^{n} \sum_{k = 1}^{∣ C ∣} y_{k}^{(i) < t >} l o g y_{k}^{(i) < t >} - \frac{1}{n} \sum_{i = 1}^{n} [\sum_{k = 1, k ̸ = j}^{∣ C ∣} y_{k}^{(i) < t >} l o g y_{k}^{(i) < t >} + y_{j}^{(i) < t >} l o g y_{j}^{(i) < t >}]$

下面来求导，先对第一部分

≠

k \neq j

$k ̸ = j$

求导：

∂

−

∑

≠

∣

∂

(

)

∂

⋅

∂

−

∑

≠

∣

⋅

−

(

∑

)

⋅

−

∑

≠

∣

⋅

(

−

)

⋅

∑

⋅

∑

−

∑

≠

∣

⋅

(

−

)

⋅

∑

≠

∣

⋅

\begin{array}{lcl} \frac{\partial L}{\partial Z^{<t>}_j} &=& -\sum_{k=1,k\neq j}^{|C|}\frac{\partial L^{(k)}}{\partial \widehat{y}^{<t>}_k}\cdot \frac{\partial \widehat{y}^{<t>}_k}{\partial Z^{<t>}_j}\\\\ &=&-\sum_{k=1,k\neq j}^{|C|}y_{k}^{<t>}\cdot \frac{1}{\widehat{y}_{k}^{<t>}}\cdot e^{Z_{k}^{<t>}}\cdot \frac{-1}{(\sum_{l=1}^Ce^{Z_{l}^{<t>}})^{2}}\cdot e^{Z_{j}^{<t>}}\\\\ &=&-\sum_{k=1,k\neq j}^{|C|}y_{k}^{<t>}\cdot \frac{1}{\widehat{y}_{k}^{<t>}}\cdot(-1)\cdot\frac{e^{Z_{k}^{<t>}}}{\sum_{l=1}^Ce^{Z_{l}^{<t>}}}\cdot \frac{e^{Z_{j}^{<t>}}}{\sum_{l=1}^Ce^{Z_{l}^{<t>}}}\\\\ &=&-\sum_{k=1,k\neq j}^{|C|}y_{k}^{<t>}\cdot \frac{1}{\widehat{y}_{k}^{<t>}}\cdot(-1)\cdot \widehat{y}_{k}^{<t>}\cdot \widehat{y}_{j}^{<t>}\\\\ &=&\sum_{k=1,k\neq j}^{|C|}y_{k}^{<t>}\cdot \widehat{y}_{j}^{<t>} \end{array}

$\frac{\partial L}{\partial Z _{j}^{< t >}} = = = = = - \sum_{k = 1, k ̸ = j}^{∣ C ∣} \frac{\partial L ^{(k)}}{\partial y _{k}^{< t >}} \cdot \frac{\partial y _{k}^{< t >}}{\partial Z _{j}^{< t >}} - \sum_{k = 1, k ̸ = j}^{∣ C ∣} y_{k}^{< t >} \cdot \frac{1}{y _{k}^{< t >}} \cdot e^{Z_{k}^{< t >}} \cdot \frac{- 1}{( \sum _{l = 1}^{C} e ^{Z_{l}^{< t >}} ) ^{2}} \cdot e^{Z_{j}^{< t >}} - \sum_{k = 1, k ̸ = j}^{∣ C ∣} y_{k}^{< t >} \cdot \frac{1}{y _{k}^{< t >}} \cdot (- 1) \cdot \frac{e ^{Z_{k}^{< t >}}}{\sum _{l = 1}^{C} e ^{Z_{l}^{< t >}}} \cdot \frac{e ^{Z_{j}^{< t >}}}{\sum _{l = 1}^{C} e ^{Z_{l}^{< t >}}} - \sum_{k = 1, k ̸ = j}^{∣ C ∣} y_{k}^{< t >} \cdot \frac{1}{y _{k}^{< t >}} \cdot (- 1) \cdot y_{k}^{< t >} \cdot y_{j}^{< t >} \sum_{k = 1, k ̸ = j}^{∣ C ∣} y_{k}^{< t >} \cdot y_{j}^{< t >}$

接下来对第二部分也就是

k = j

$k = j$

时，求导：

(

)

∂

−

∂

(

)

∂

⋅

∂

−

⋅

∑

−

⋅

(

∑

)

−

⋅

(

∑

−

)

(

∑

)

−

⋅

∑

⋅

(

−

∑

)

−

⋅

(

−

)

−

⋅

(

−

)

\begin{array}{lcl} \frac{\partial L^{(j)}}{\partial Z^{<t>}_j} &=& -\frac{\partial L^{(j)}}{\partial \widehat{y}^{<t>}_j}\cdot \frac{\partial \widehat{y}^{<t>}_j}{\partial Z^{<t>}_j}\\\\ &=&-y_{j}^{<t>}\cdot \frac{1}{\widehat{y}_{j}^{<t>}}\cdot \frac{e^{Z_{j}^{<t>}}\cdot \sum_{l=1}^Ce^{Z_{l}^{<t>}} – e^{Z_{j}^{<t>}}\cdot e^{Z_{j}^{<t>}}}{(\sum_{l=1}^Ce^{Z_{l}^{<t>}})^{2}}\\\\ &=&-y_{j}^{<t>}\cdot \frac{1}{\widehat{y}_{j}^{<t>}}\cdot \frac{e^{Z_{j}^{<t>}}\cdot (\sum_{l=1}^Ce^{Z_{l}^{<t>}} – e^{Z_{j}^{<t>}})}{(\sum_{l=1}^Ce^{Z_{l}^{<t>}})^{2}}\\\\ &=&-y_{j}^{<t>}\cdot \frac{1}{\widehat{y}_{j}^{<t>}}\cdot\frac{e^{Z_{j}^{<t>}}}{\sum_{l=1}^Ce^{Z_{l}^{<t>}}}\cdot (1 – \frac{e^{Z_{j}^{<t>}}}{\sum_{l=1}^Ce^{Z_{l}^{<t>}}})\\\\ &=&-y_{j}^{<t>}\cdot \frac{1}{\widehat{y}_{j}^{<t>}}\cdot \widehat{y}_{j}^{<t>}\cdot (1 – \widehat{y}_{j}^{<t>})\\\\ &=&-y_{j}^{<t>}\cdot (1 -\widehat{y}_{j}^{<t>}) \end{array}

$\frac{\partial L ^{(j)}}{\partial Z _{j}^{< t >}} = = = = = = - \frac{\partial L ^{(j)}}{\partial y _{j}^{< t >}} \cdot \frac{\partial y _{j}^{< t >}}{\partial Z _{j}^{< t >}} - y_{j}^{< t >} \cdot \frac{1}{y _{j}^{< t >}} \cdot \frac{e ^{Z_{j}^{< t >}} \cdot \sum _{l = 1}^{C} e ^{Z_{l}^{< t >}} - e ^{Z_{j}^{< t >}} \cdot e ^{Z_{j}^{< t >}}}{( \sum _{l = 1}^{C} e ^{Z_{l}^{< t >}} ) ^{2}} - y_{j}^{< t >} \cdot \frac{1}{y _{j}^{< t >}} \cdot \frac{e ^{Z_{j}^{< t >}} \cdot ( \sum _{l = 1}^{C} e ^{Z_{l}^{< t >}} - e ^{Z_{j}^{< t >}} )}{( \sum _{l = 1}^{C} e ^{Z_{l}^{< t >}} ) ^{2}} - y_{j}^{< t >} \cdot \frac{1}{y _{j}^{< t >}} \cdot \frac{e ^{Z_{j}^{< t >}}}{\sum _{l = 1}^{C} e ^{Z_{l}^{< t >}}} \cdot (1 - \frac{e ^{Z_{j}^{< t >}}}{\sum _{l = 1}^{C} e ^{Z_{l}^{< t >}}}) - y_{j}^{< t >} \cdot \frac{1}{y _{j}^{< t >}} \cdot y_{j}^{< t >} \cdot (1 - y_{j}^{< t >}) - y_{j}^{< t >} \cdot (1 - y_{j}^{< t >})$

现在把两部分相加起来，得到：

∂

∑

≠

∣

⋅

[

−

⋅

(

−

)

]

∑

≠

∣

⋅

−

∑

∣

⋅

−

⋅

∑

∣

−

\begin{array}{lcl} \frac{\partial L}{\partial Z^{<t>}_j} &=&\sum_{k=1,k\neq j}^{|C|}y_{k}^{<t>}\cdot \widehat{y}_{j}^{<t>} + [-y_{j}^{<t>}\cdot (1 -\widehat{y}_{j}^{<t>})]\\\\ &=& \sum_{k=1,k\neq j}^{|C|}y_{k}^{<t>}\cdot \widehat{y}_{j}^{<t>} + \widehat{y}_{j}^{<t>}\cdot \widehat{y}_{j}^{<t>} – y_{j}^{<t>}\\\\ &=&\sum_{k=1}^{|C|}y_{k}^{<t>}\cdot \widehat{y}_{j}^{<t>} – y_{j}^{<t>}\\\\ &=&\widehat{y}_{j}^{<t>}\cdot \sum_{k=1}^{|C|}y_{k}^{<t>}- y_{j}^{<t>}\\\\ &=&\widehat{y}_{j}^{<t>} – y_{j}^{<t>} \end{array}

$\frac{\partial L}{\partial Z _{j}^{< t >}} = = = = = \sum_{k = 1, k ̸ = j}^{∣ C ∣} y_{k}^{< t >} \cdot y_{j}^{< t >} + [- y_{j}^{< t >} \cdot (1 - y_{j}^{< t >})] \sum_{k = 1, k ̸ = j}^{∣ C ∣} y_{k}^{< t >} \cdot y_{j}^{< t >} + y_{j}^{< t >} \cdot y_{j}^{< t >} - y_{j}^{< t >} \sum_{k = 1}^{∣ C ∣} y_{k}^{< t >} \cdot y_{j}^{< t >} - y_{j}^{< t >} y_{j}^{< t >} \cdot \sum_{k = 1}^{∣ C ∣} y_{k}^{< t >} - y_{j}^{< t >} y_{j}^{< t >} - y_{j}^{< t >}$

这里解释下上面这个公式导数第二部怎么化为倒数第一步的，其实也就是

∣

\sum_{k=1}^{|C|}y_{k}^{<t>}

$\sum_{k = 1}^{∣ C ∣} y_{k}^{< t >}$

为什么是

1

$1$

，因为

y_{k}^{<t>}

$y_{k}^{< t >}$

是真实值，在

C

$C$

个里面，只有一个类别为1，其它都是0,（想想 one-hot），所以和为1。

接下来，我们就可以很容易的得到

∂

\frac{\partial L}{\partial a^{<t>}}

$\frac{\partial L}{\partial a ^{< t >}}$

，因为我们设的

Z^{<t>}=W_{ya}a^{<t>} + b_y

$Z^{< t >} = W_{y a} a^{< t >} + b_{y}$

，所以：

∂

⋅

∂

(

−

)

⋅

\begin{aligned} \frac{\partial L}{\partial a^{<t>}} &= \frac{\partial L}{\partial Z^{<t>}}\cdot \frac{\partial Z^{<t>}}{\partial a^{<t>}}\\\\ &=(\widehat{y}^{<t>} – y^{<t>})\cdot W_{ya} \end{aligned}

$\frac{\partial L}{\partial a ^{< t >}} = \frac{\partial L}{\partial Z ^{< t >}} \cdot \frac{\partial Z ^{< t >}}{\partial a ^{< t >}} = (y^{< t >} - y^{< t >}) \cdot W_{y a}$

∂

⋅

∂

(

−

)

⋅

\begin{aligned} \frac{\partial L}{\partial W_{ya}} &= \frac{\partial L}{\partial Z^{<t>}}\cdot \frac{\partial Z^{<t>}}{\partial W_{ya}}\\\\ &=(\widehat{y}^{<t>} – y^{<t>})\cdot a^{<t>} \end{aligned}

$\frac{\partial L}{\partial W _{y a}} = \frac{\partial L}{\partial Z ^{< t >}} \cdot \frac{\partial Z ^{< t >}}{\partial W _{y a}} = (y^{< t >} - y^{< t >}) \cdot a^{< t >}$

因此，整个bp推导结束，关于

\frac{1}{n}

$\frac{1}{n}$

一般是要加上的，原因前面也讲过了，不过这就是个常数，对于求导没有任何影响，我们在实现的时候加上。

四、梯度裁剪（gradient clipping）

前面已经把RNN的知识点全部介绍完了，但是训练RNN的过程并不总是那么愉快，我们总是希望loss随着迭代次数的进行是像蓝线那样不停的下降，然而事实却是绿线那样，直到你看到loss抛出了NaN。（图片来自李宏毅RNN课件）。

产生梯度爆炸和消失的原因是因为RNN中经常出现像下图所示那样

陡峭的悬崖

（loss对参数的变化）（图片来自李宏毅RNN），如下图所示，幸运的情况下我们更新梯度后正好是在平面上，这时loss在缓缓的下降，但不幸的时候参数（w1，w2）直接跳上了悬崖，这就会导致loss暴增，下面如果再跳下来，loss又会爆减，这就对应了上图中的绿色曲线。

但是最不幸的是有时候正在踩在悬崖峭壁上，然后下面就是直接飞出去了，导致loss直接Nan了。

这样的话RNN就没法继续训练下去了。

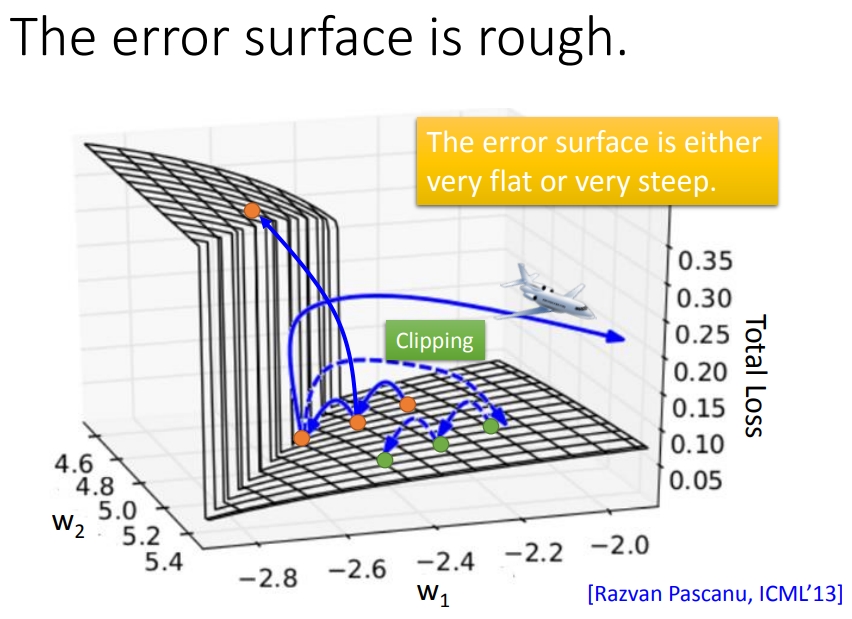
Mikolov大神（word2vec的发明者）最早想出了解决办法，这就是

梯度裁剪（Gradient Clipping）

。其实梯度裁剪的思想相当的直白和简单，但是能想出来并且work就已经是件很厉害的事情了。

梯度裁剪的思想是：如果梯度大于某个阈值或者小于阈值的负数，就用直接让它等于阈值。

比如，设置阈值为10，那么如果求得的梯度如果大于10，或者小于-10，则直接设置梯度为10。这样做的好处显而易见，回到上面的图，飞出去的那条线，就是因为梯度太大或者太小导致参数更新后，loss爆了，采用梯度裁剪后，会使得飞出去的线变成虚线所示，继续落在面上，可以继续训练。

五、RNN的实现

注：实现部分参考ng的deep learning课堂作业，关于RNN的实现，有一个点需要注意的，因为我们每个句子（单词）的长度是不同的，所以有两种方法去处理：

1.对句子（单词）进行对齐，自己设置对齐长度（可以设置为长度最长的单词，不足的用一个标记符来填充，比如keras中可使用pad_sequences()函数来截长补短），但这样做在计算loss的时候需要注意，因为计算每一个timestamp的loss的时候填充的标记符不能计算，可以自己设置个mask矩阵来标记计算的时候忽略那些填充符号。现在为了矩阵并行计算，大多使用这种方法。

2.不对句子（单词）进行对齐，但在做前向后向的时候要一个一个样本的去做，也就是for循环遍历样例，这样做计算量上大一点。ng的作业即采用这种方法。

这篇博客应用场景依然采用ng作业，即生成恐龙的名字，所以采用第二种方法。有时间的话，也会实现第一种方法，毕竟第一种方法主流些。

接下来就是RNN的实现，难点主要在bp上，实现bp有个技巧，因为链式法则，（不怎么好描述，直接举个例子），假如

y= t^2

$y = t^{2}$

，

t = 4x + 1

$t = 4 x + 1$

，如果我们想求

∂

\frac{\partial y}{\partial x}

$\frac{\partial y}{\partial x}$

，根据链式法则，

∂

⋅

∂

\frac{\partial y}{\partial x} = \frac{\partial y}{\partial t} \cdot \frac{\partial t}{\partial x}

$\frac{\partial y}{\partial x} = \frac{\partial y}{\partial t} \cdot \frac{\partial t}{\partial x}$

，如果在给定

∂

\frac{\partial y}{\partial t}

$\frac{\partial y}{\partial t}$

的情况，我们就不用管他前面无论有多少级联，都不用管，我们只要求

∂

\frac{\partial t}{\partial x}

$\frac{\partial t}{\partial x}$

就可以了。所以，我们实现的时}候，传入的参数就是上一级的梯度就可以了（如下图所示，如果给定

da^{<2>}

$d a^{< 2 >}$

（两条红线），我们就不用管它后面的级联了，写代码的时候只要把

da^{<2>}

$d a^{< 2 >}$

当参数传进来就可以了），只要实现本cell（层）的参数的求导就ok了。

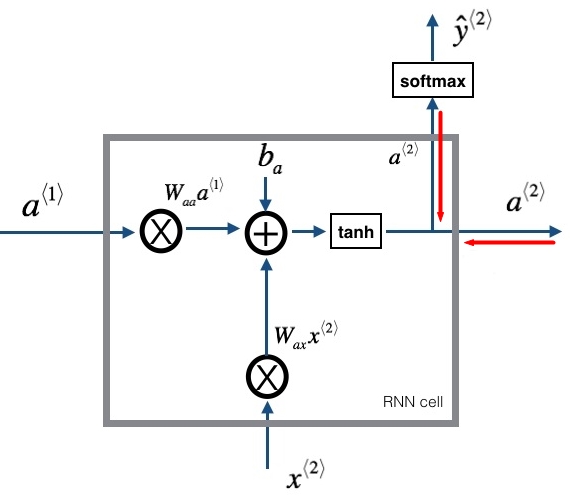
关于基本RNN网络的实现，主要有参数初始化、前向传播、后向传播、参数更新（+梯度裁剪）这四部分。

5.1 参数初始化

def initialize_parameters(n_a, n_x, n_y):
	"""
	Initialize parameters with small random values
	Returns:
	parameters -- python dictionary containing:
				  Wax -- Weight matrix multiplying the input, of shape (n_a, n_x)
				  Waa -- Weight matrix multiplying the hidden state, of shape (n_a, n_a)
				  Wya -- Weight matrix relating the hidden-state to the output, of shape (n_y, n_a)
				  b --  Bias, of shape (n_a, 1)
				  by -- Bias relating the hidden-state to the output, of shape (n_y, 1)
	"""
	np.random.seed(1)
	Wax = np.random.randn(n_a, n_x) * 0.01  # input to hidden
	Waa = np.random.randn(n_a, n_a) * 0.01  # hidden to hidden
	Wya = np.random.randn(n_y, n_a) * 0.01  # hidden to output
	ba = np.zeros((n_a, 1))  # hidden bias
	by = np.zeros((n_y, 1))  # output bias
	parameters = {"Wax": Wax, "Waa": Waa, "Wya": Wya, "ba": ba, "by": by}

	return parameters

5.2 前向传播

单个cell的实现：

def rnn_step_forward(xt, a_prev, parameters):
	"""
	Implements a single forward step of the RNN-cell that uses a tanh activation function
	Arguments:
	xt -- the input data at timestep "t", of shape (n_x, m).
	a_prev -- Hidden state at timestep "t-1", of shape (n_a, m)
	**here, n_x denotes the dimension of word vector, n_a denotes the number of hidden units in a RNN cell
	parameters -- python dictionary containing:
				  Wax -- Weight matrix multiplying the input, of shape (n_a, n_x)
				  Waa -- Weight matrix multiplying the hidden state, of shape (n_a, n_a)
				  Wya -- Weight matrix relating the hidden-state to the output, of shape (n_y, n_a)
				  ba --  Bias,of shape (n_a, 1)
				  by -- Bias relating the hidden-state to the output,of shape (n_y, 1)
	Returns:
	a_next -- next hidden state, of shape (n_a, 1)
	yt_pred -- prediction at timestep "t", of shape (n_y, 1)
	"""
	# get parameters from "parameters"
	Wax = parameters["Wax"] #(n_a, n_x)
	Waa = parameters["Waa"] #(n_a, n_a)
	Wya = parameters["Wya"] #(n_y, n_a)
	ba = parameters["ba"]   #(n_a, 1)
	by = parameters["by"]   #(n_y, 1)

	a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
	yt_pred = softmax(np.dot(Wya, a_next) + by) #(n_y,1)
	
	return a_next, yt_pred

整个前向传播过程：

def rnn_forward(X, Y, a0, parameters, vocab_size=27):
	x, a, y_hat = {}, {}, {}
	a[-1] = np.copy(a0)
	# initialize your loss to 0
	loss = 0
	for t in range(len(X)):
		# Set x[t] to be the one-hot vector representation of the t'th character in X.
		# if X[t] == None, we just have x[t]=0. This is used to set the input for the first timestep to the zero vector.
		x[t] = np.zeros((vocab_size, 1))
		if (X[t] != None):
			x[t][X[t]] = 1
		# Run one step forward of the RNN
		a[t], y_hat[t] = rnn_step_forward(parameters, a[t - 1], x[t]) #a[t]: (n_a,1), y_hat[t]:(n_y,1)
	    # Update the loss by substracting the cross-entropy term of this time-step from it.
		#这里因为真实的label也是采用onehot表示的，因此只要把label向量中1对应的概率拿出来就行了
		loss -= np.log(y_hat[t][Y[t], 0])

	cache = (y_hat, a, x)

	return loss, cache

5.3 后向传播

def rnn_step_backward(dy, gradients, parameters, x, a, a_prev):

	gradients['dWya'] += np.dot(dy, a.T)
	gradients['dby'] += dy
	Wya = parameters['Wya']
	Waa = parameters['Waa']
	da = np.dot(Wya.T, dy) + gradients['da_next']  #每个cell的Upstream有两条，一条da_next过来的，一条y_hat过来的
	dtanh = (1 - a * a) * da  # backprop through tanh nonlinearity
	gradients['dba'] += dtanh
	gradients['dWax'] += np.dot(dtanh, x.T)
	gradients['dWaa'] += np.dot(dtanh, a_prev.T)
	gradients['da_next'] = np.dot(Waa.T, dtanh)

	return gradients


def rnn_backward(X, Y, parameters, cache):
	# Initialize gradients as an empty dictionary
	gradients = {}

	# Retrieve from cache and parameters
	(y_hat, a, x) = cache
	Waa, Wax, Wya, by, ba = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['ba']

	# each one should be initialized to zeros of the same dimension as its corresponding parameter
	gradients['dWax'], gradients['dWaa'], gradients['dWya'] = np.zeros_like(Wax), np.zeros_like(Waa), np.zeros_like(Wya)
	gradients['dba'], gradients['dby'] = np.zeros_like(ba), np.zeros_like(by)
	gradients['da_next'] = np.zeros_like(a[0])

	# Backpropagate through time
	for t in reversed(range(len(X))):
		dy = np.copy(y_hat[t])
		dy[Y[t]] -= 1 #计算y_hat - y,即预测值-真实值，因为真实值是one-hot向量，只有1个1，其它都是0，
		# 所以只要在预测值（向量）对应位置减去1即可，其它位置减去0相当于没变
		gradients = rnn_step_backward(dy, gradients, parameters, x[t], a[t], a[t - 1])

	return gradients, a

5.4 参数更新

#梯度裁剪
def clip(gradients, maxValue):
	'''
	Clips the gradients' values between minimum and maximum.
	Arguments:
	gradients -- a dictionary containing the gradients "dWaa", "dWax", "dWya", "db", "dby"
	maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue
	Returns:
	gradients -- a dictionary with the clipped gradients.
	'''
	dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['dba'], gradients['dby']
	# clip to mitigate exploding gradients, loop over [dWax, dWaa, dWya, dba, dby].
	for gradient in [dWax, dWaa, dWya, dba, dby]:
		np.clip(gradient, -maxValue, maxValue, gradient)
	gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": dba, "dby": dby}
	return gradients

#更新梯度
def update_parameters(parameters, gradients, lr):
	parameters['Wax'] += -lr * gradients['dWax']
	parameters['Waa'] += -lr * gradients['dWaa']
	parameters['Wya'] += -lr * gradients['dWya']
	parameters['ba']  += -lr * gradients['dba']
	parameters['by']  += -lr * gradients['dby']
	return parameters

到这里，RNN（基于生成单词的这个场景）基本写完了，在生成单词这个任务场景里，每一个时间步都要基于前面的字符生成一个字符，每一步的输出是softmax向量（概率分布），表示字符表里每个字符的概率，我们需要采样得到下一个字符。下面是采样的代码：

def sample(parameters, char_to_ix, seed):
	"""
	Sample a sequence of characters according to a sequence of probability distributions output of the RNN
	Arguments:
	parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b.
	char_to_ix -- python dictionary mapping each character to an index.
	seed -- used for grading purposes. Do not worry about it.
	Returns:
	indices -- a list of length n containing the indices of the sampled characters.
	"""

	# Retrieve parameters and relevant shapes from "parameters" dictionary
	Waa, Wax, Wya, by, ba = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['ba']
	vocab_size = by.shape[0]
	n_a = Waa.shape[1]
	# Step 1: Create the one-hot vector x for the first character (initializing the sequence generation).
	x = np.zeros((vocab_size, 1))
	# Step 1': Initialize a_prev as zeros
	a_prev = np.zeros((n_a, 1))

	# Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate
	indices = []

	# Idx is a flag to detect a newline character, we initialize it to -1
	idx = -1

	# Loop over time-steps t. At each time-step, sample a character from a probability distribution and append
	# its index to "indices". We'll stop if we reach 50 characters (which should be very unlikely with a well
	# trained model), which helps debugging and prevents entering an infinite loop.
	counter = 0
	newline_character = char_to_ix['\n']

	while (idx != newline_character and counter != 50):
		# Step 2: Forward propagate x using the equations (1), (2) and (3)
		a = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + ba)
		z = np.dot(Wya, a) + by
		y = softmax(z)

		# for grading purposes
		np.random.seed(counter + seed)

		# Step 3: Sample the index of a character within the vocabulary from the probability distribution y
		idx = np.random.choice(vocab_size, p = y.ravel())  # 等价于np.random.choice([0,1,...,vocab_size-1], p = y.ravel())，
		# 一维数组或者int型变量，如果是数组，就按照里面的范围来进行采样，如果是单个变量，则采用np.arange(a)的形式
		# Append the index to "indices"
		indices.append(idx)
		# Step 4: Overwrite the input character as the one corresponding to the sampled index.
		#每次生成的字符是下一个时间步的输入
		x = np.zeros((vocab_size, 1))
		x[idx] = 1

		# Update "a_prev" to be "a"
		a_prev = a
		# for grading purposes
		seed += 1
		counter += 1
	if (counter == 50):
		indices.append(char_to_ix['\n'])

	return indices

完整的代码以及数据集（dinos.txt）地址：

https://github.com/tz28/deep-learning/blob/master/rnn.py

数据集：

https://github.com/tz28/deep-learning/blob/master/dinos.txt

后记：因为实习的缘故，这篇博客拖了整整两个月才写完…，希望以后不要这样了。

原文链接：https://blog.csdn.net/u012328159/article/details/84962285

RNN（recurrent neural network）（二）——动手实现一个RNN

你可能也喜欢