1.背景
PCA算法主要用于降维,将高维的特征映射到低维的空间中。假设,我没有20个数据,每个数据特征100维,即(20,100)。通过降维,我们可以将100维的特征降到10维,即(20,10)这样就大大减小了计算量。
一般,降维后的特征数不超过样本数
2.最大方差理论
信号处理中,认为信号的是高方差的,噪声是低方差的,信噪比就是信号和噪声的反差比,越大越好。我们降维到k个特征,就是选取前k个特征向量(根据特征值从大到小排序好)。第一条坐标轴就是覆盖数据最大方差的位置,第二条坐标轴就是垂直于最大第一条轴的方向。。。。。。
3.图片理解
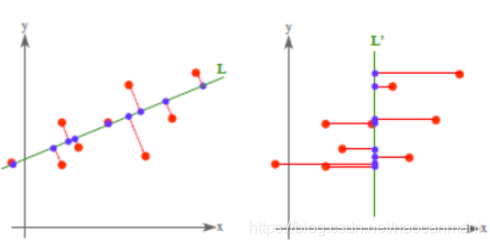
(图片来源
https://blog.csdn.net/jiaoyangwm/article/details/79805939
)
对于PCA来说其实就是找一个超平面,使得样本到超平面的距离最小
特点
:PCA方法是
无监督
的,不用设置参数,没有考虑样本的标签,没有利用已有的先验知识。
小的特征值只是说明相应维度上样本分布的方差小,并不代表它对分类的作用小
。某些极端情况下,PCA舍去的特征可能恰恰包含了对分类极其重要的信息。基于Fisher准则的可分性分析就是使用训练样本的标签来降维,最大程度地保留可分性信息。
(
https://blog.csdn.net/jiaoyangwm/article/details/79805939
)
3.算法步骤
- 将每个特征进行零均值化,即每个特征减去该特征的均值,比如上面的例子(20,100)有100个特征,对每一列求均值
- 求出协方差矩阵
- 求出协方差矩阵的特征值及对应的特征向量r
- 将特征向量按对应特征值大小从上到下按行排列成矩阵(按特征值从大到小),取前k行组成矩阵P
- 原始数据和矩阵P相乘就能得到降维后的数据
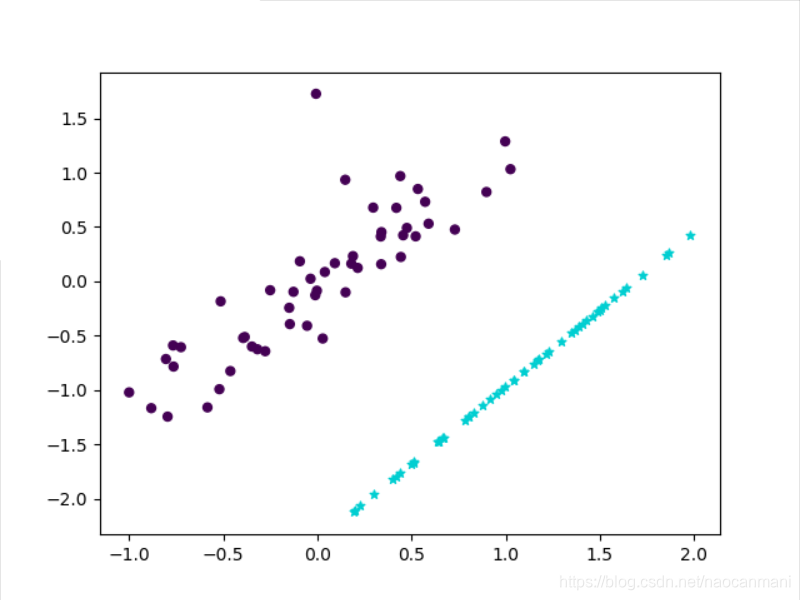
import numpy as np
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
# 二维降到一维
def pca(data, k): # (nums, features)
d_mean = np.mean(data, axis=0)
data -= d_mean
cov_data = np.cov(data.T) # 计算协方差,(f,n)->(f,f)
val, vec = np.linalg.eig(cov_data) # 计算特征值和特征向量
val_arg = np.argsort(val)
val_arg = val_arg[::-1]
vec_sorted = vec[:,val_arg] # 一列是一个特征向量
vec_s = vec_sorted[:,0:k]
datas = np.dot(data, vec_s) # 压缩后数据
data_y = np.dot(datas, vec_s.T) + d_mean # 还原
return datas, data_y
X1, Y1 = make_classification(n_features=2, n_redundant=0, n_informative=2,
n_clusters_per_class=1)
ind_y = np.where(Y1 == 0)[0]
X1 = X1[ind_y]
Y1 = Y1[ind_y]
datas, data_y = pca(X1,1)
plt.scatter(X1[:, 0], X1[:, 1], marker='o', c=Y1,
s=25, edgecolor='k')
plt.scatter(data_y[:, 0], data_y[:, 1], marker='*', c='#00CED1',
s=25, edgecolor='k')
plt.show()
错误之处烦请指正