读论文 Spyros Blanas, Yinan Li, Jignesh M. Patel: Design and evaluation of main memory hash join algorithms for multi-core CPUs. SIGMOD Conference 2011: 37-48
1. 背景
如今硬件发展非常迅速,摩尔定律指出”集成电路上可容纳的晶体管数目,约每隔两年就会增加一倍“。虽然目前硬件性能的增长速度稍稍放缓,但是仍具有较大的发展潜力。随着硬件的不断发展,内存越来越便宜,将全部数据存放在内存中进行处理变得可能。同时,处理器的并行能力也日益增长,CPU的核数越来越多。基于此背景,研究新型处理器架构下的并行哈希连接算法变得非常有意义。
2. 介绍
2.1 存储体系
计算机的存储体系呈现一种金字塔型,金字塔底层的是容量大、价格便宜但是速度慢的存储设备;顶层是速度快,但是容量小、价格昂贵的存储设备。中央处理器(CPU)、缓存(Cache)和内存(Memory)分别位于金字塔的前3层,处理数据的速度自顶向下依次递减,容量依次递增,如图2.1所示。

图2.1 存储体系的金字塔结构
当CPU请求数据时,会在Cache中先查看是否存在请求的数据。若存在请求数据,则将数据返回给CPU,称该过程为Cache命中;若Cache中不存在请求的数据,则需要从内存中查找,称该过程为Cache丢失。由于访问Cache的速度远高于访问内存的速度,因此我们希望Cache命中数越多越好。
2.2 线程同步
多核处理器的优势在于,它能使用多个线程同时对数据进行处理,加快程序执行的速度。然而,多个线程可能对同一个内存地址进行读写操作,这可能会导致数据不一致等问题。为了解决这些问题,需要引入线程同步机制,保证每块内存区域在一个时刻只能被一个线程修改。线程同步会带来很多额外的代价,例如线程通信、锁的竞争等。
2.3 影响性能的因素
对于内存中的并行哈希连接算法来说,影响其性能的因素主要有两点:一是在连接操作时,需要从内存中读取相应数据,由于访问Cache的速度远高于访问内存的速度,因此希望在CPU读取数据时,Cache丢失越少越好;二是利用多线程并行加速算法,必然要考虑同步的代价,我们希望同步量越少越好。综上,设计并行哈希连接算法主要综合考虑Cache丢失和同步这两种代价。
3. 哈希连接
并行的哈希连接算法主要有分区(Partition)、构建哈希表(Build)以及探测(Probe)三个操作,其中分区操作不是所有的哈希连接算法锁必须的。事实上,关于在现代硬件架构上分区操作是否有益于哈希连接具有较大的争论。分区操作的目的是减少Cache丢失,一种观点认为,现代的硬件架构很好地屏蔽了cache丢失带来的影响,而分区操作会引入很多不必要的同步代价,并且分区数的多少对算法性能影响较大,这使得分区的哈希连接算法鲁棒性不够强,因此哈希连接算法要舍弃分区这一操作;另一种观点则持有相反的态度,支持该观点的学者认为,Cache丢失仍然是影响算法性能的重要因素,因此在设计算法时仍然需要分区来减少cache丢失。关于这两种观点的具体内容,我们将在接下来的章节详细叙述。
3.1 Partition
分区(Partition)操作是将数据利用哈希函数划分到不同区域上的操作,这一操作的目的是减少算法在Probe阶段的cache丢失
分区操作可以分为非阻塞式分区(Non-blocking Partitioning)和阻塞式分区(Blocking Partitioning)两种。Non-blocking Partitioning只扫描一遍关系表R,对于每个元组,计算好该元组所在的分区后直接将数据写入该分区。而Blocking Partitioning则需要多次扫描关系表R,计算好每个分区的大小,以及所有元组所在的分区后,统一将数据写入对应位置。
3.1.1 非阻塞式分区
非阻塞式分区(Non-blocking Partitioning)的好处是其只需要扫描一次关系表R,但是由于将R中元组写入分区的过程是并发的,在将元组写入对应分区时各线程需要同步,这会带来额外的代价。
非阻塞式分区方法有两种实现方法,一种是共享分区法(Shared Partition),另一种是独立分区法(Private Partition)。
共享分区
共享分区(Shared Partition)算法首先会创建p个分区,所有线程对所有数据同步进行分区操作(此处分区p的数量和Cache大小有关,目的是使针对于每个分区建立的哈希表能够存入CPU的Cache中以减小Build阶段Cache缺失的次数,p的大小不能太大,如果太大会导致TLB缺失,CPU将频繁访问内存页,导致性能下降)。首先为每个线程划分一部分数据,每个线程计算其负责的数据中各个元组连接键的哈希值。根据哈希值的计算结果,将各个元组写入对应的分区。为了保证同一个内存地址在同一时刻只能被一个线程写,需要注意各个线程之间的同步。共享分区算法如图3.1所示。

图3.1 基于共享分区的哈希连接算法示意图
独立分区
独立分区(Private Partition)算法则为对每个线程分配一部分数据,每个线程将其负责的数据划分到其私有的分区上,当所有线程都完成工作后,将各个线程的私有分区合并。这种方法的好处在于,每个线程划分私有分区时不需要任何同步操作。这样做的坏处也十分明显,由于过多的分区被创建,CPU要频繁地与内存交换数据。独立分区算法如图3.2所示。
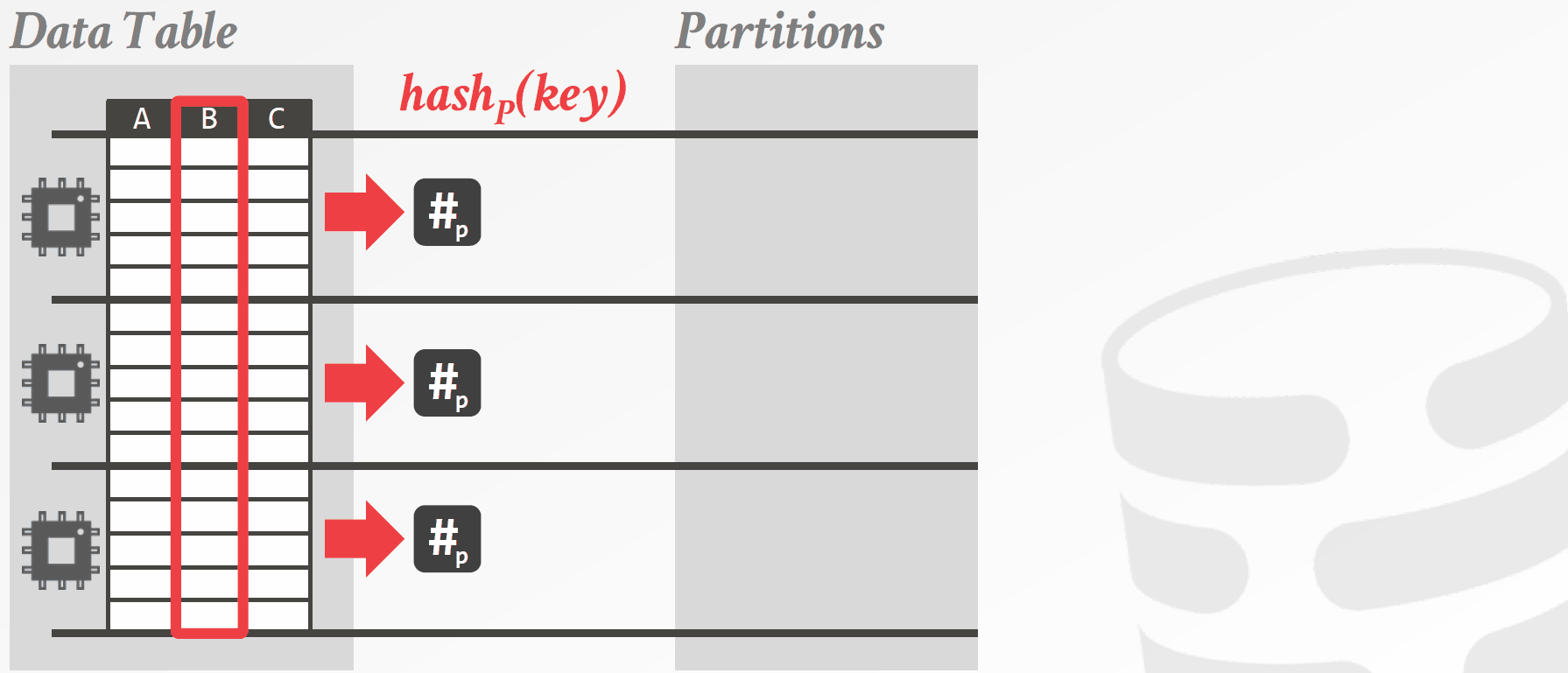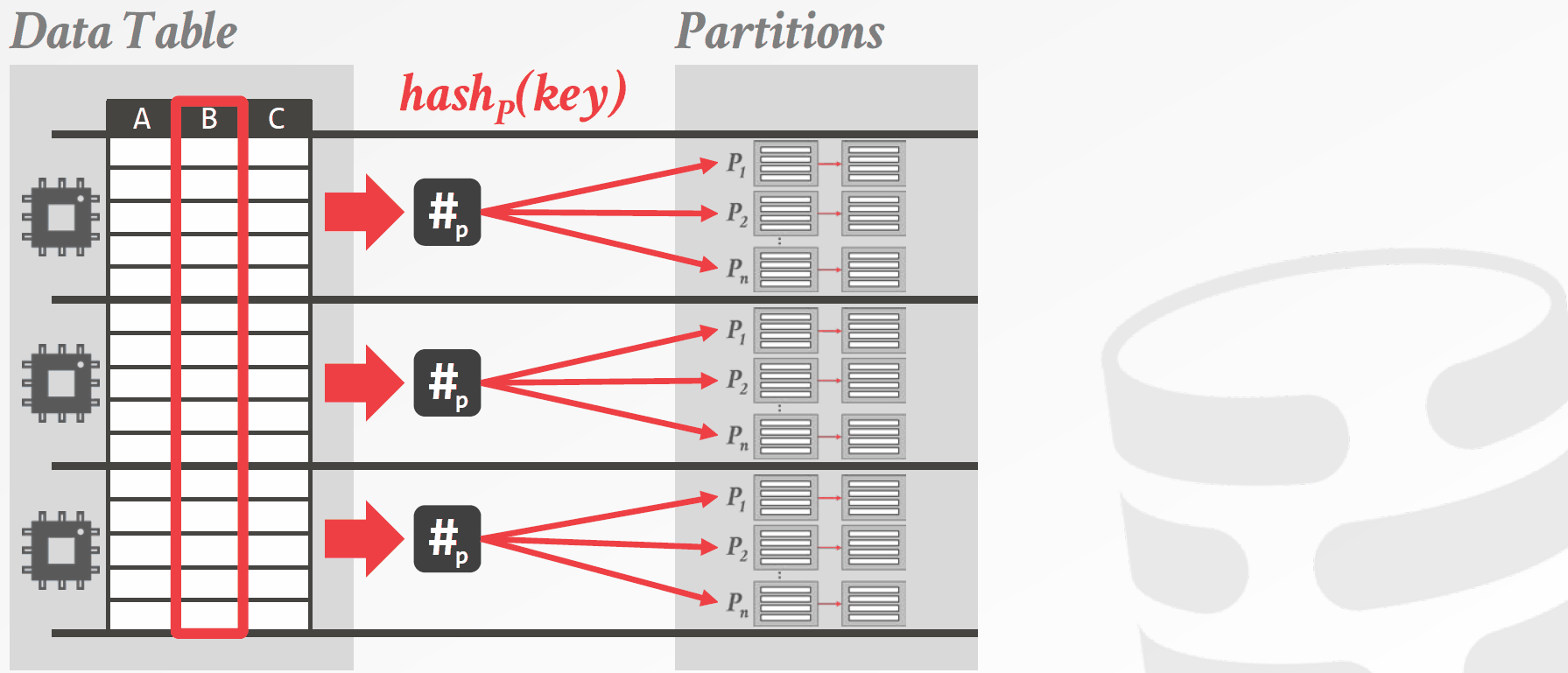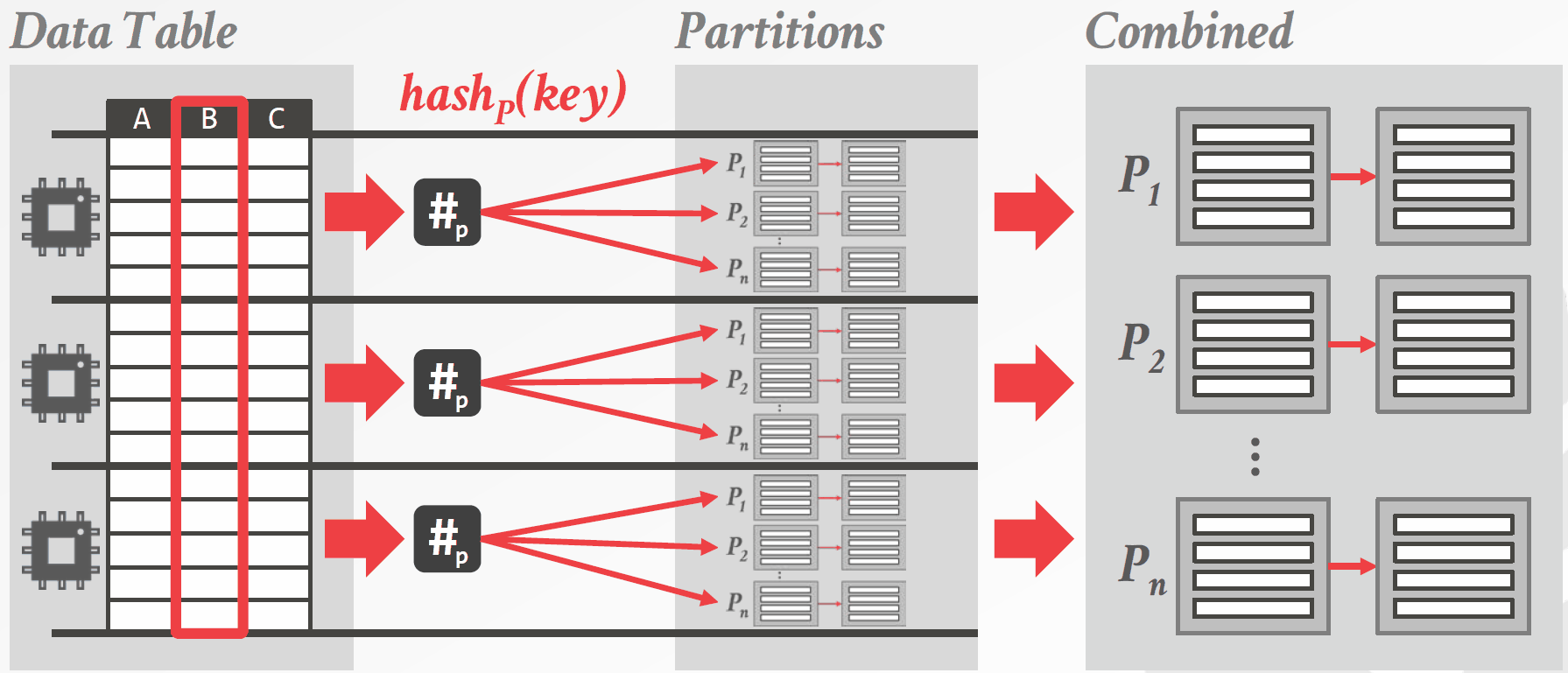
图3.2 基于独立分区的哈希连接算法示意图
3.1.2 阻塞式分区
阻塞式分区(Blocking Partitioning)的好处在于,它不需要同步的代价,并且可以限定每次分区操作的分区数量,可以避免分区数过多带来的问题。但与此同时,这种算法必须在扫描关系表R上付出更多的代价。
Radix分区是一种阻塞式的分区方法,其具体做法如下(如图3.3所示):
-
为每个线程分配一部分数据,每个线程计算一个“直方图”,直方图统计的是每个线程中各个分区中元组的数量,分区的依据是连接键对应的数位,选取哪一个数位可以视情况而定。
-
每个分区计算好直方图后,通过计算前缀和的方法将所有直方图合并,这样就能得到每个分区中元组的数量,根据元组的数量为每个分区分配空间。
-
再次扫描整个R表,将元组写到对应位置,由于已经计算好每个分区的大小,因此可以确定每个元组在分区中的位置,这样多个线程同时操作时不需要同步。
-
对每个分区重复以上操作,直到得到预期的分区数。
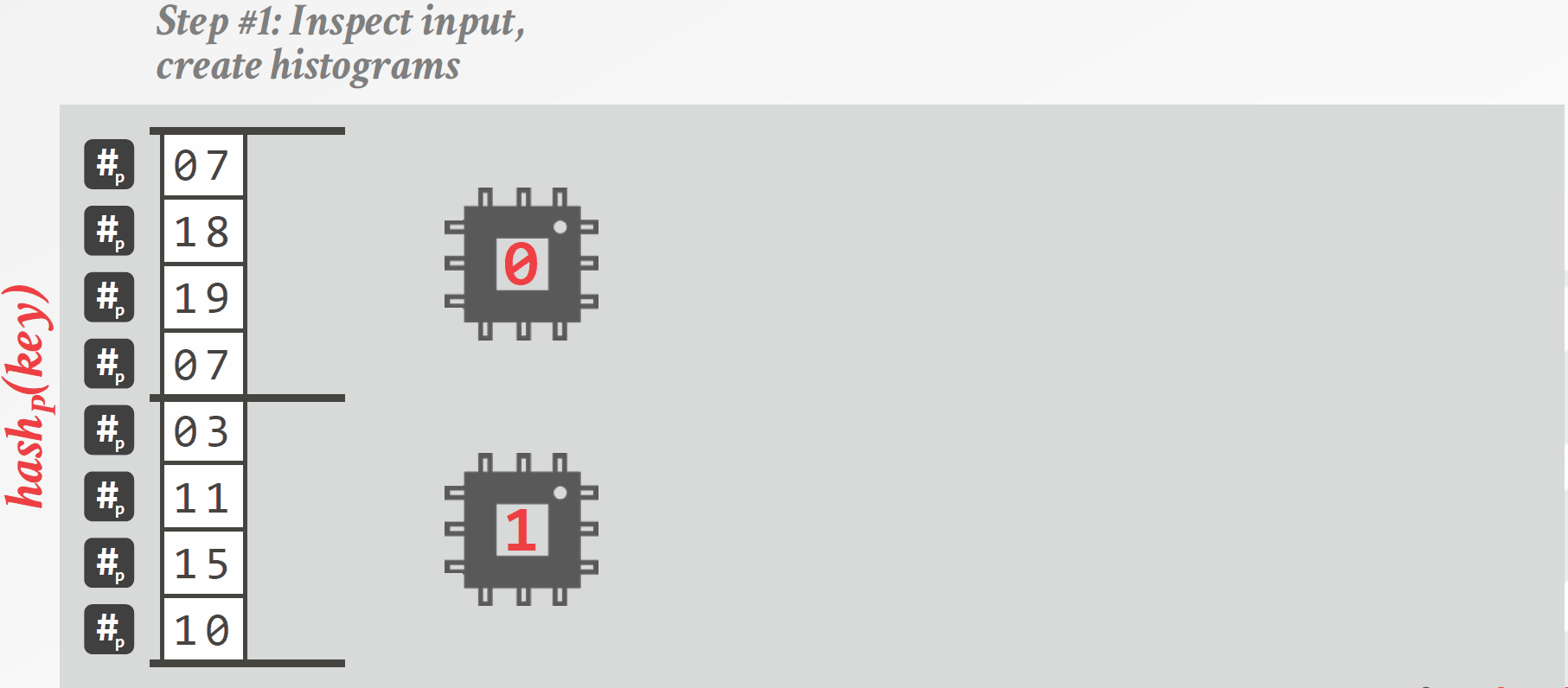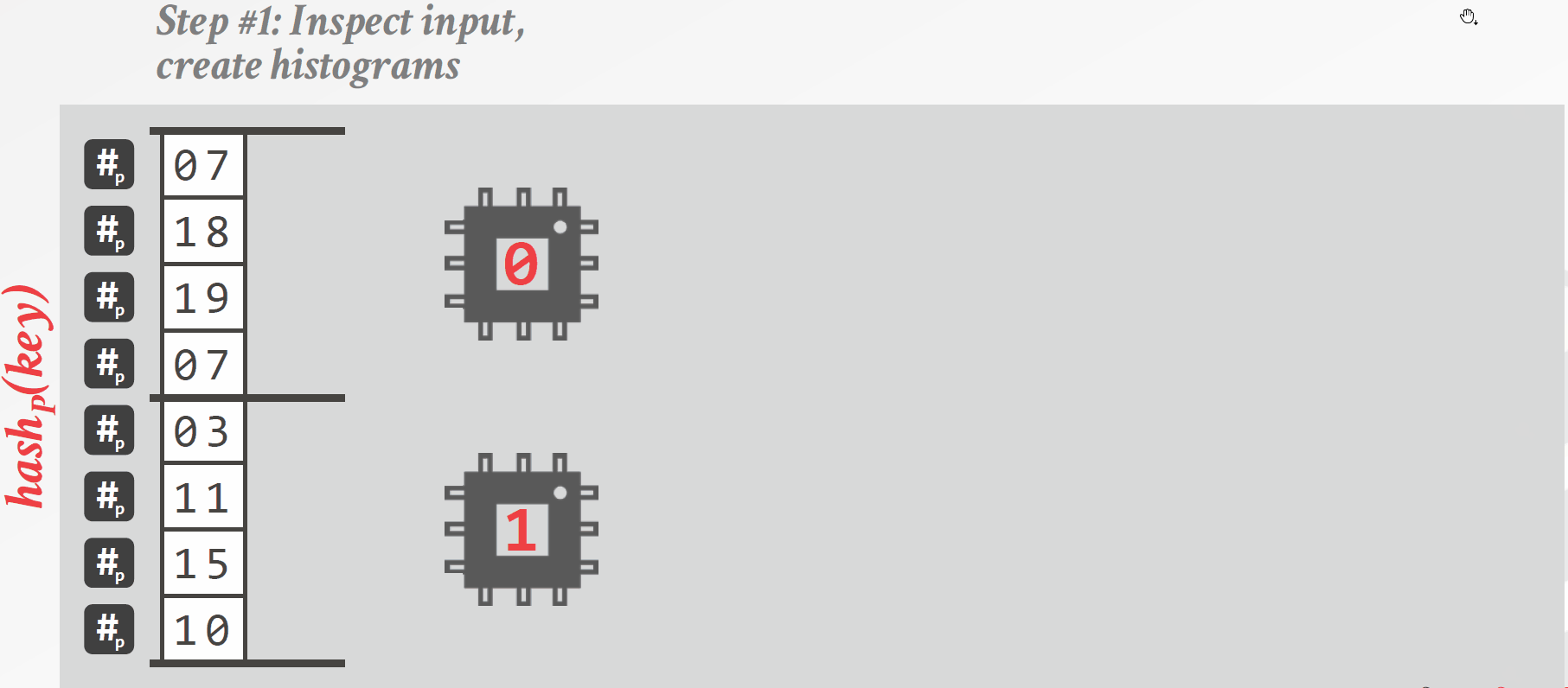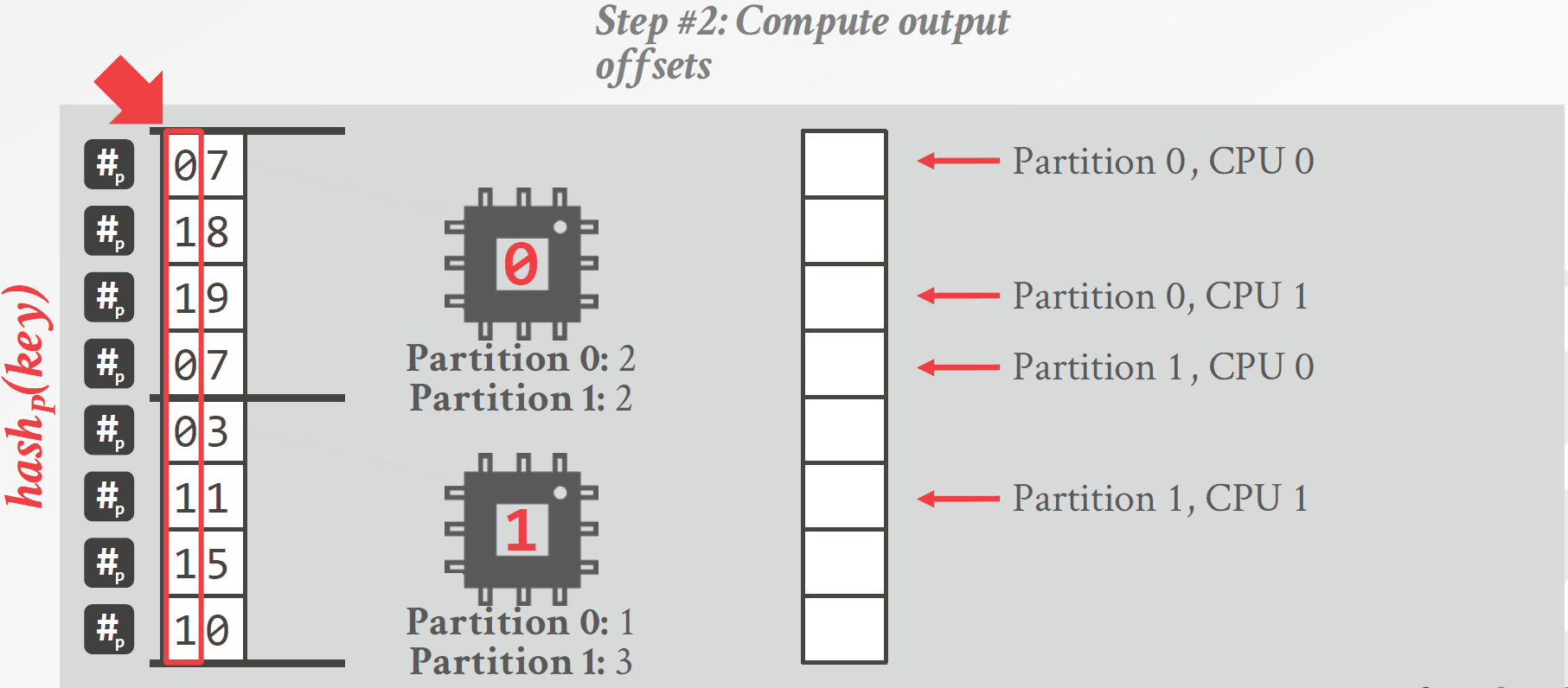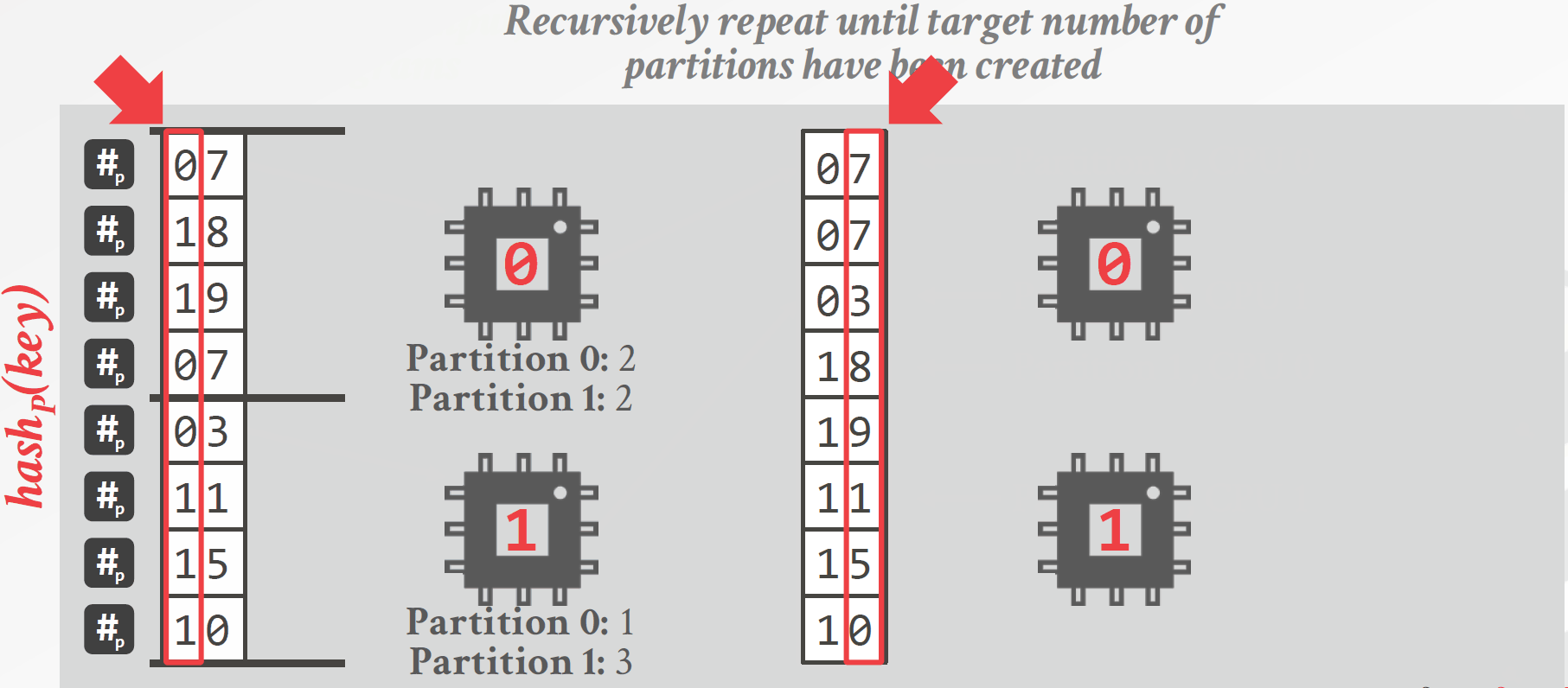
图3.3 基于Radix分区的哈希连接算法
3.2 Build
Build是构建哈希表的阶段,对于R表中的每一个元组,计算其连接键的哈希值,然后将其加入哈希表中。对于hash join算法来说,分区操作不是必须的。分区与否导致Build阶段略有不同。
* 如果之间没有分区操作,则所有n个线程都同步操作R表
* 如果之前有过分区,总共有n个线程,则线程i操作分区Ri+0*n,Ri+1*n,…。例如,若n=8时,则线程0就操作分区R0,R8,…。
对于Build阶段来说,影响其性能的因素主要有哈希函数和哈希表的选取。
3.2.1 哈希函数
在连接算法中,我们通常倾向于选择运算速度快,哈希冲突少的哈希函数。常用的哈希函数有以下几种:
* Murmur Hash:是一种非加密型的哈希函数,由Austin Appleby在2008年提出。Murmur Hash有很多变种,包括MurmurHash2和MurmurHash3。Murmur Hash的特点是运算性能高,冲突率低。
* Google CityHash:CityHash是由Google在2011年提出的一种哈希函数,它基于MurmurHash2进行了改进,在计算小于64字节的键值时速度更快。
* Google FarmHash:FarmHash是Google在2014年提出针对CityHash的一个改进版本,它比CityHash的冲突率更低。
* CLHash:这种哈希函数是2016年提出的一种新型哈希函数,主要是针对carry-less multiplication指令进行优化。
3.2.2 哈希表
哈希算法通过哈希函数计算键的哈希值,根据哈希值将所需查询的数据映射到哈希表中一个位置来访问记录。哈希表对于哈希算法的性能又较大的影响,根据需不同需求可以设计不同的哈希表。
常见的哈希表有以下几种:
* 链式哈希表:链式哈希把所有哈希值一样的元素放在一个链表上,这种做法的好处是简单,插入很快,但是查找时需要在对应的链表上扫描一遍,因此查找比较慢。
* 开放寻址哈希:发生冲突时,根据哈希函数探查其他的地址,若发现所有可以被探查到的地址都已经被占用,则插入失败。探查的方法又分为线性探查法、二次探查以及双重散列探查等方法。
* Cuckoo哈希:主要思想是利用多个哈希函数,建立多个哈希表,每次计算多个哈希值。例如使用2个哈希函数,要插入一个新元素时:
(1)若两个位置均为空,则任选一个插入;
(2)若两个位置中一个为空,则插入到空的那个位置;
(3)若两个位置均不为空,则将其中一个位置原来的元素踢出,插入当前元素,被踢出的元素重 新调用该算法。
3.3 Probe
探测(Probe)阶段是将关系表S利用哈希表与R连接的过程。对于表S中的每一个元组,假设它的连接键为k,在哈希表中查找到哈希值为h(k)的桶,然后将该桶中和k相匹配的元组与它做作连接。
和Build 阶段类似,有分区的哈希连接Probe阶段和不分区的哈希连接Probe阶段也不一样。
* 如果之间没有分区操作,则所有n个线程都同步操作S表
* 如果之前有过分区,总共有n个线程,则线程i操作分区Si+0*n,Si+1*n,…。例如,若n=8时,则线程0就操作分区S0,S8,…。
3.4 小结
不分区的哈希连接算法就是各个线程同时读取R表数据分片,然后使用哈希函数将所有的数据写到一张共享的哈希表上,最后在Probe阶段,对于每个S表中的元组,去哈希表上查找与它相匹配的元组连接操作。
分区的hash join算法首先利用哈希函数对数据分区,然后各个线程在各个分区上建立哈希表,Probe阶段也是先将S利用哈希函数进行分区,然后在对应的分区上查找相匹配的R元组进行连接。
4. 性能评估
前面提到并行的哈希算法有多种实现方式:可以包含分区操作,也可以不包含分区操作;可以使用阻塞式的分区方法,也可以使用非阻塞式的分区方法;可以使用共享分区,也可以使用独立分区。那么这些哈希连接算法到底哪种表现更好,分别适用于哪些环境?接下来通过实验来解答这些问题。
4.1 实验环境
使用两种不同的硬件架构,一种是基于Intel Nehalem架构的Intel Xeon X5650处理器,Nehalem架构是Intel公司在2008年推出的一种新型中央处理器微架构。Intel Xeon X5650有六个内核,每个内核有2个线程,L3缓存大小为12M,Cache Line的大小为64字节,详细参数如表4.1所示。
表4.1 Intel Xeon X5650参数表
另一种硬件架构是Sun Microsystems公司于2007年推出的一种微处理器UltraSPARC T2,该处理器有8个内核,每个内核最多可以同时管理8个线程。其L2 cache的大小为4M,Cache Line大小和Intel Xeon X5650一样是64字节,详细参数如表4.2所示。
表4.2 UltraSPARC T2参数表
4.2 实验数据集
数据集中R表的大小为16M,S表的大小为256M。每个元组大小为16bytes,键的大小为8bytes。为了测试各种哈希连接算法在不同的数据分布下的表现,分别使用3组数据来测试算法性能。这3组数据集分别是均匀分布的数据集、略微倾斜的数据集以及极度倾斜的数据集。
均匀分布的数据集是指S中的每一个元组,以相同概率匹配R中的元组。而倾斜数据集是在S表中加入数据,使S表中外键的分布倾斜。倾斜的程度依照数据Zipf分布的参数来判断:略微倾斜指参数s大小为1.05;极度倾斜指参数s大小为1.25。
4.3 实验结果
4.3.1 各种分区算法在均匀数据集上的表现
通过测试不同算法在均匀分布上运行的CPU时钟周期,比较算法的性能。并使用不同的分区数,测试有分区算法的最优分区数以及对分区数的敏感程度。结果如图4.1所示,坐标轴的横轴为分区数量,对于不分区的算法把分区数为1。
图4.1 各种连接算法在均匀数据上的表现
从图4.1中可以发现,对于有分区的算法来说,当分区的数量与cache line大小相适应的时候,算法性能最佳。同时可以发现,不分区的算法与最佳参数时的有分区算法表现相当。并且有分区的算法对分区数量十分敏感,尤其是当分区数量过多时,算法的性能急剧下降。这是因为当分区数量过多时,每个线程都会创建与分区数量相同的缓冲区,这会带来如下两个问题:
(1) 大部分缓冲区中只有少量甚至没有数据,会导致大量的空间浪费
(2) cache的大小有限,无法存下所有的缓冲区,这导致内存和cache之间进行频繁的数据交换,算法性能下降。
分区数量过多带来算法性能的下降并不会影响基于Radix分区的哈希连接算法,因为Radix分区在每一趟操作都限制了分区的数量,因此性能不会如同非阻塞式分区一样急剧下降。
4.3.2 各种分区算法在倾斜数据集上的表现
为了验证不同算法对于数据分布的敏感性, 调整S表中外键的数据分布。当数据略微倾斜时,即S表中外键的数据分布符合参数为1.05的Zipf分布时,实验结果如图4.2所示。
图4.2 各种连接算法在略微倾斜的数据集上的表现
从图4.2中可以看出,当数据不均匀的时候,不分区的算法性能有所提升,而基于共享分区的算法性能略有下降。
继续加大数据的倾斜程度,使S表的外键符合参数为1.25的Zipf分布,得到如图4.3的实验结果。可以发现,当数据倾斜程度增加时,不分区的算法性能进一步提升,而基于共享分区的算法性能进一步下降。由此可以得出结论:不分区的算法可以很好地处理数据不均匀的情况。这是因为分布不均匀的数据局部性较好,cache命中率较高。而对于基于分区的连接算法来说,在分区操作时,大部分操作集中在处理数量较多的键上,引起锁竞争,造成算法性能下降。
图4.3 各种连接算法在高度倾斜的数据集上的表现
4.3.3 连接算法各阶段性能分析
哈希连接算法通常可以分为Partition、Build和Probe3个阶段。这里通过计算各种连接算法在不同阶段的性能表现来分析影响算法性能的因素。均匀数据集下,各种连接算法在各个阶段的具体表现如表4.3所示,其中,”No”表示不分区的连接算法,”SN”表示使用和线程数一致的独立分区算法,”L2-S”和”L2-R”分别表示分区数为2048的情况下基于共享分区的连接算法和基于Radix分区的连接算法。这里取2048是根据图4.1所示的最优分区数。
表4.3 各种连接算法在均匀数据集上的性能
从表4.3中可以看出,不分区的连接算法在Probe阶段由于大量的cache丢失导致耗费的时间较长,而使用与线程数一致的独立分区算法由于分区数太少,对于cache丢失并没有明显改善,因此Probe阶段的代价依然较高。分区数为2048的基于共享分区的连接算法和基于Radix分区的连接算法在Partition阶段的花费较高,而在Probe阶段由于Cache命中率高使得花费较低。这与我们的预期相符。
当数据分布不均匀的时候,如表4.4所示,各种算法的cache丢失都有所下降,这也证明了数据局部性强带来的好处。
表4.4 各种连接算法在倾斜数据集上的性能
比较”SN”和”NO”的性能计数,可以发现”SN”在Probe阶段的花费竟然比”NO”更高。另外”L2-S”和”L2-R”在均匀数据上的cache丢失和TLB丢失要比处理倾斜数据集时高,但是处理倾斜数据时的速度却低于处理均匀数据,这与我们的预期不符。造成这种现象可能的原因是现代CPU架构较为复杂,一些其它因素带来的cache丢失难以捕捉,并且线程同步带来的锁开销会导致算法性能降低。
4.3.4 同步多线程加速
同步多线程(Simultaneous Multi-Threading, SMT)是一种在1个CPU时钟周期内,能够执行来自多个线程指令的硬件多线程技术。同步多线程使多个独立执行的线程能够更好地利用处理器资源。
为了比较同步多线程机制对各种连接算法的加速效果,通过比较各连接算法在不同的线程数下的表现来测试算法的可扩展性。实验结果如图4.4所示。
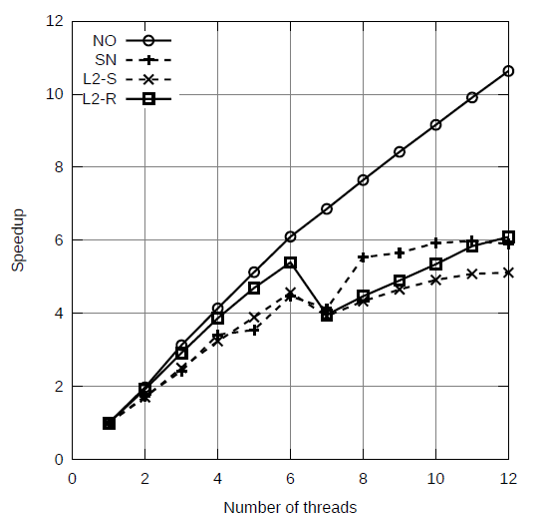
图4.4 不同线程数对各种连接算法的加速效果
从图4.4中可以看出同步多线程机制对不分区的算法加速效果最好,并且在线程数少于6个时,各种连接算法的性能都线性提升。而当线程数为7个时,有分区算法的性能都有所下降,这种性能的下降是由负载不均衡导致的。当线程数持续增加时,有分区的连接算法的性能又有所提高。
不同线程数下各种连接算法处理速度,以及增加线程带来的提升如表4.5和表4.6所示。其中表4.5是在Intel Nehalem架构上算法的表现,表4.6是在Sun UltraSPARC T2上的表现。从中可以看出,使用多线程同步对于各种连接算法的性能都有所提升,尤其是对于不分区的连接算法。通过对比不同数据分布下的算法性能,可以发现在高度不均匀的数据上受益不如均匀分布的数据,这是因为高度不均匀的数据cache丢失原本就低于均匀分布的数据,所以加速效果不明显。
表4.5 在Intel Nehalem架构下使用多线程同步,各算法的运行速度(单位为10亿指令周期)
表4.6 在Sun UltraSPARC架构下使用多线程同步,各算法的运行速度(单位为10亿指令周期)
4.3.4 同步和负载均衡
不分区的哈希连接算法只在Build阶段涉及同步操作,而从表4.3和表4.4中可以看出,Build阶段的时间只占整个过程的不到2%,因此同步的代价可以忽略不计。而对于有分区的哈希连接算法,同步则会带来较高的代价。图4.5所示的是Radix Join各个线程运行的情况。从图中可以看出,所有的线程必须等待最慢的线程完成工作才能进行下一阶段的操作,这会导致很大程度上的资源浪费。
图4.5 Radix Join算法过程中各个线程的运行状态
为了避免线程“空等”的问题,我们希望每个线程等待的时间尽量少,速度快的线程承担更重的任务,速度慢的线程负责更少的任务,并且完成工作的线程可以帮助其它线程。也就是说考虑负载均衡,来减少算法的总运行时间。加入负载均衡的机制后,算法的性能如图4.6所示。
图4.6 加入负载均衡机制后Radix Join算法过程中各个线程的运行状态
5 总结
通过实验对比不分区的哈希连接算法和有分区的哈希连接算法,可以发现,现代的CPU架构在使用了SMT等机制后很好地隐藏了cache丢失的问题,cache丢失对于算法性能的影响并不是特别大。因此为了应对cache丢失问题提出的有分区哈希连接算法,由于需要较多的同步代价,因此性能不如不分区的算法。并且不分区的算法鲁棒性更强,因为它几乎不需要根据硬件参数的变化而调整自身的参数。于此同时,使用有分区的哈希连接算法还需考虑负载均衡等问题,这也增加了算法实现的难度。因此,在现代CPU架构下,不分区的哈希连接算法在某种程度上要优于有分区的哈希连接算法。
以上实验和观点均来自于论文:
Spyros Blanas, Yinan Li, Jignesh M. Patel: Design and evaluation of main memory hash join algorithms for multi-core CPUs. SIGMOD Conference 2011: 37-48
至于这个观点是否正确我不得而知,只是在另一篇论文中,明确反驳了该观点:
C. Balkesen, et al., Main-Memory Hash Joins on Multi-Core CPUs: Tuning to the Underlying Hardware
参考资料
[1]
摩尔定律维基百科
[2]
存储体系维基百科
[3]
CMU Advanced Database System Lecture
[4]
散列表维基百科
[5]
Nehalem微架构 维基百科