fpga的希尔伯特变换实现
零.实现背景
因为今明工作项目需要使用到希尔伯特变换来处理问题,所以顺便就把设计流程和代码都整理下来,以便供他人使用。选用Xilinx的7系列板子,Vivado平台。
一.希尔伯特实现的基本原理
希尔伯特变换的物理意义十分简单:把信号的所有频率分量的相位推迟90度
希尔伯特变换器是频幅特性为1的全通滤波器,其正频率负90相移,其负频率正90相移
希尔伯特具体实现的方法用两种
–
1. 实信号,通过fft这样可以得到
精确
的的解析函数结果,但是缺点就是必须是按照帧去计算的
可以看下这个链接:
希尔伯特变换
序列xr的解析信号具有单边傅里叶变换。也就是说,对于负频率,变换消失了。为了近似分析信号,希尔伯特计算:具体可以看matlab的hilbert()函数
–
输入序列(一般来说为实数序列)的FFT,
–
将对应于负频率的FFT系数用零替换
,
–
并计算结果的反FFT
。
–
得到的复数实部为原始信号,虚部为相移信号
–
2.实信号,通过希尔伯特滤波器去实现,缺点是得到的是近似的结果,但优点是可以连续的输入数据,而不是按照帧去计算。
希尔伯特滤波器的构造,可以看着个链接
fpga希尔伯特实现
,这个是参照XILINX fir手册写的。
希尔伯特滤波器其实是幅度为1的全通滤波器,可以用FIR实现,也可以用IIR实现,但工程上大多使用FIR,对于偶次的FIR滤波器,必须在0h和Fs/2处降为0,且必须为带通滤波器
下图中:采样频率为1M ,通带我50kHz – 450kHz

而对于奇次的滤波器,则0hz增益为0,且必须是高通滤波器。

二.fpga实现
因为项目要求的数据帧长度很大,远远超过FPGA的fft核最大长度65536,而且板子资源也比较紧张,最后选择是使用FIR希尔伯特滤波器实现的方案。
1)matlab仿真
- 使用FDATOOL 工具去构造滤波器,选取阶数采用偶数 ,因为通带纹波的大小与阶数成反比,设定小于0.1db 也就是千分之5的变化。

但是得到滤波器系数去带入matlab程序,并不能完成我的项目任务。
因为我的输入信号本身就是加在100K调制信号上的,而且十分微弱,这点增益的变化还是会带来项目的失败
。又因为随着阶数的改变,在我调制信号的频率上增益的有时正有时负,
项目中必须是正值才能完成任务
,一点衰减都不行。
最后不断调试决定为8阶
,

反而满足项目需求,
这样告诉我一件事,根据理论大胆假设细致验证问题找原因才是关键
。
又因为matlab是浮点数计算,fpga采样定点数做滤波器(
采用浮点数滤波器延迟打拍的资源根本无法估量
)所以会带来精度损失,有可能带来设计的失败,所以需要做定点仿真,看是否满足要求
-
定点仿真
:采用杜勇老师《matlab与fpga的滤波器实现》源码改了改
%matlab定点仿真
fs=1000000; %采样频率
load('Num8.mat'); %Num8为滤波器系数
h_pm = Num;
%滤波系数进行量化
h_pm12=round(h_pm/max(abs(h_pm))*(2^11-1));%12bit量化
h_pm14=round(h_pm/max(abs(h_pm))*(2^13-1));%14bit量化
hn=h_pm14;
%转换进制
q14_hex_pm=dec2hex(h_pm14+2^14*(h_pm14<0));
%求滤波器的幅频响应
fid=fopen('D:\E4_6_hf10_14.txt','w');
fprintf(fid,'%8d\r\n',h_pm);fprintf(fid,';');
fclose(fid);
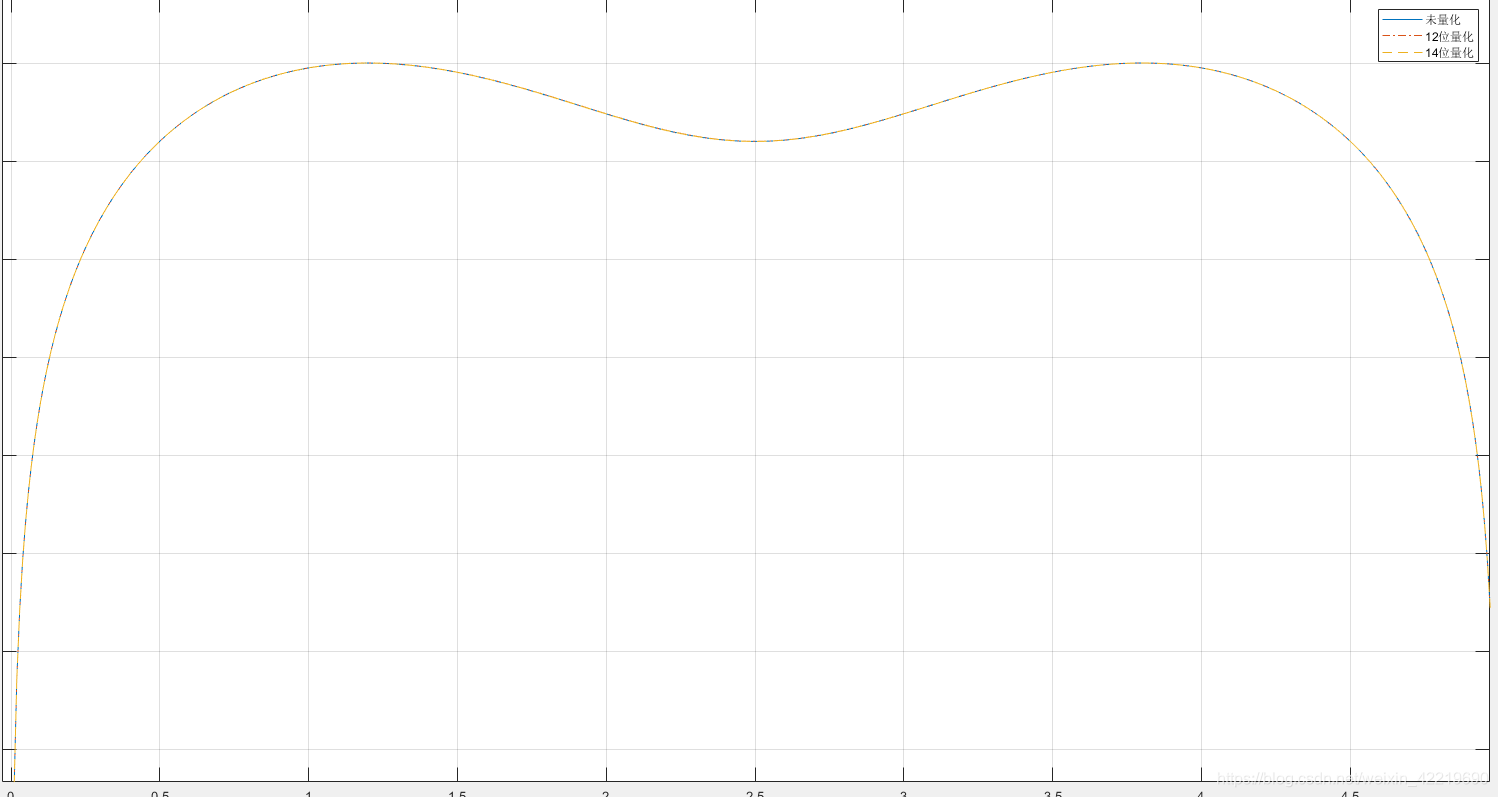
可以看到100K 左右几乎没有变化
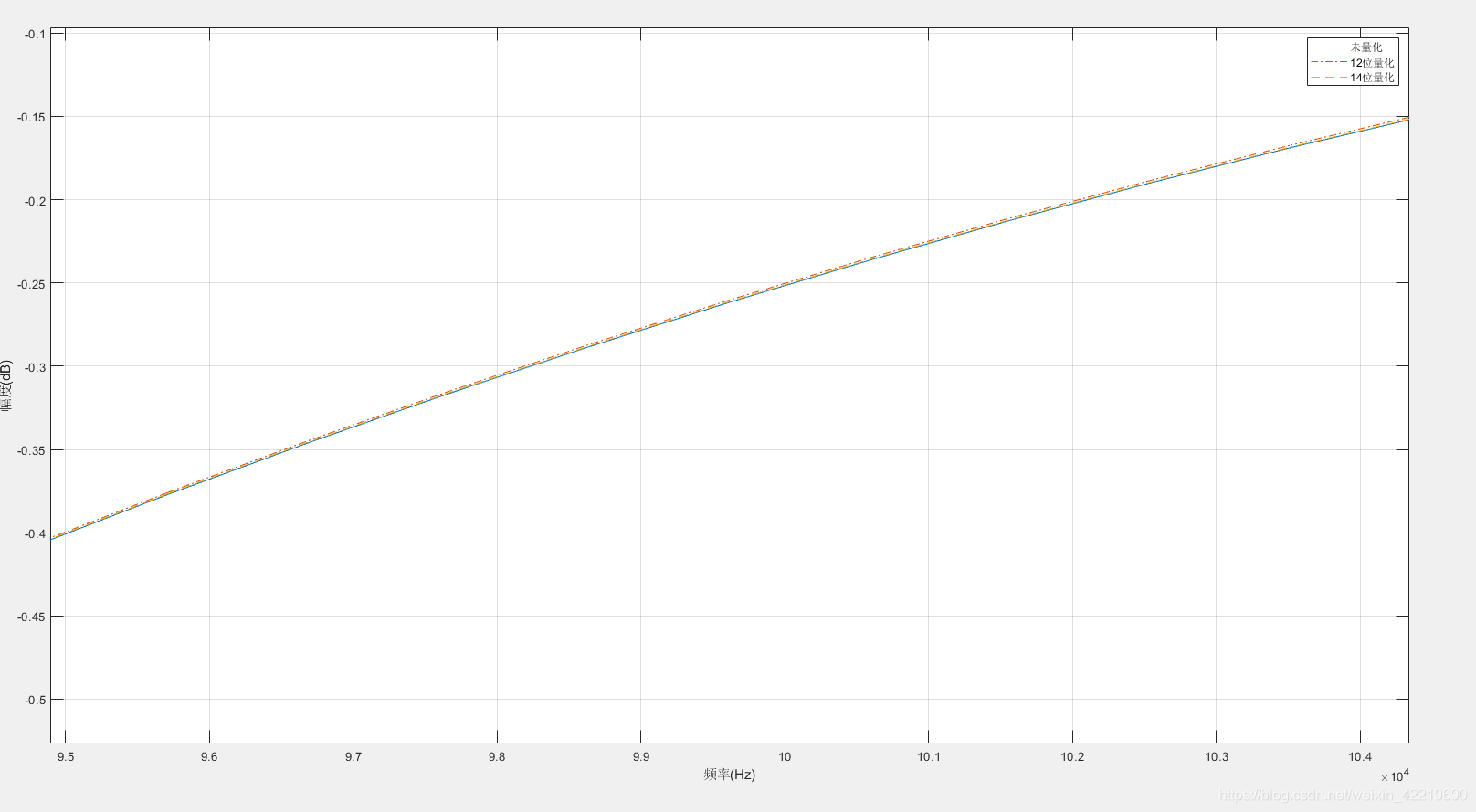
但是这里与FDATOOL工具的幅值是不同的,我觉得matlab应该没有错,应该是杜勇老师代码哪里可能有一些漏洞吧,具体我也没时间找,就是个验证工具而已。
fir滤波器比iir设计方便好处就是
:因为没有反馈,只需要考虑滤波器系数量化位宽,不需要考虑输入数据位宽,但资源使用多。而IIR因为有反馈结构,需要对输入数据位宽和滤波器系数量化位宽,还有输出位宽同时考虑,仿真工作需要做的多些,但资源利用少,而且FPGA实现没有现成的IP核使用,只能手动去做。
2)fpga滤波器实现
最后选择12位宽实现:0 -782 0 -2047 0 2047 0 782 0
实现成本:
每个滤波器 8个延迟单元,通过叠加时结构
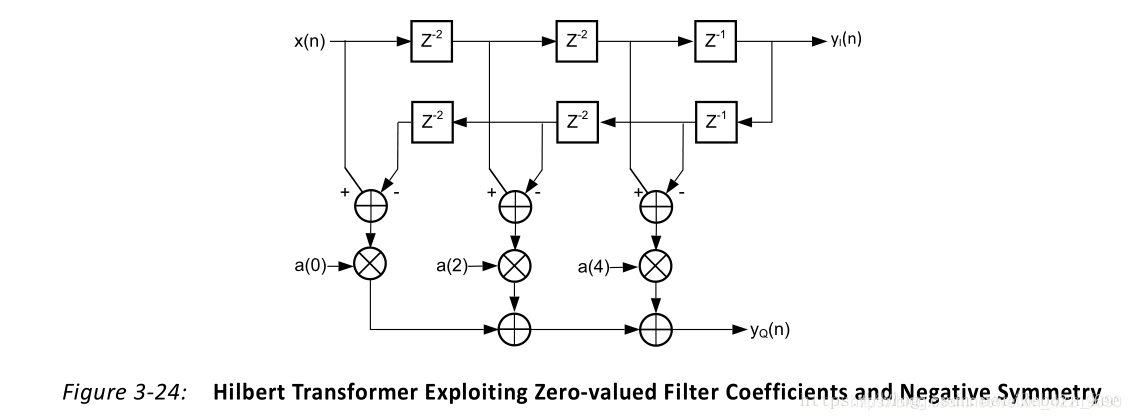
需要3个加法器,2个乘法器,
计算成本
:几乎可以不计
资源成本
:16位输入 12位权值 ,需要3 * 16 * 12= 576个全加器,乘法单元使用fpga中集成DSP。如果把频率拉高做串行滤波器那几乎根本没什么消耗。
fpga实现采用VIvado的FIR的IP核,
这个IP核在2015你以后就没更新过,可能代表做个滤波器也没啥吧,关键还是matlab仿真,当然也可以是用System Generater 中 simulink 的Xilinx组件,这个可以做定点与浮点的仿真对比,而且有一个好处就是自动导入系数,而IP核导入COE文件最大只支持32位,超过这个只能手打,非常之坑,对于高阶的滤波器设计建议使用它,会简短设计流程。因为只有8位我就没用。
-
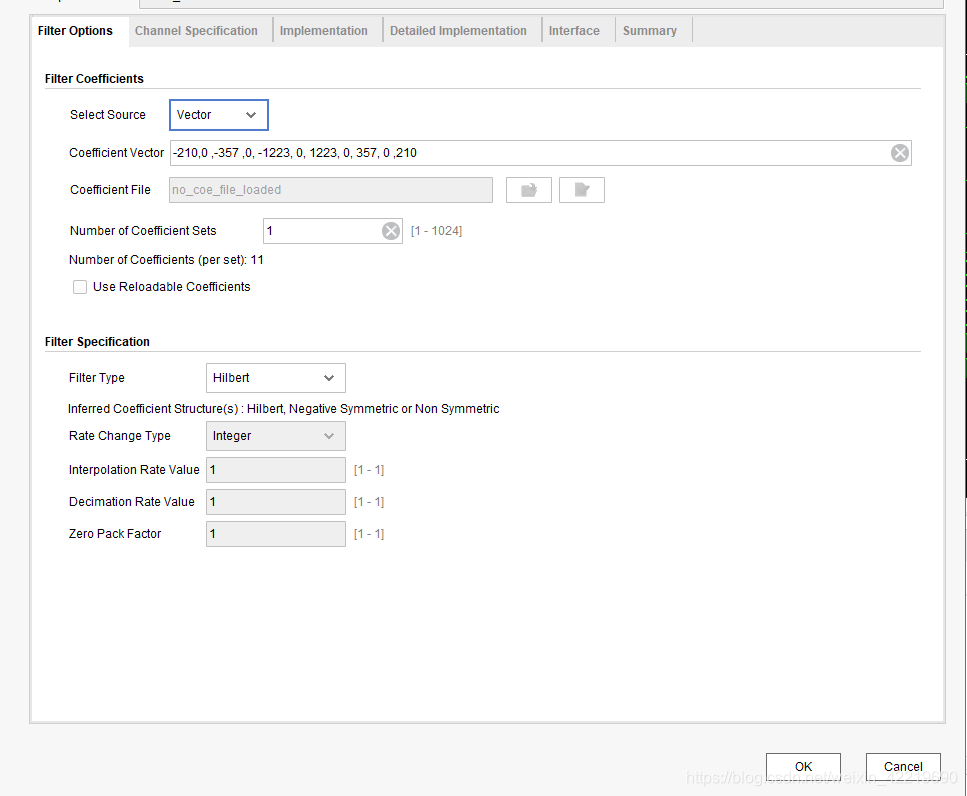
打开IP核 ,具体设置直接上网上找有非常之多资料,注意选择Hilbert结构,只有选择才能综合成折叠式结构,减少成本。
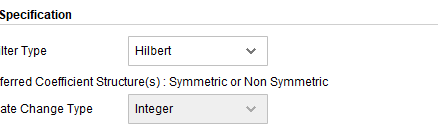
注意
: - 有时候滤波器系数量化后不为0,你需要把很小的量化值改成0才行,要不你用不了。
-
其次你们是否发现Xilinx优化的结构把系数的是采用第二位优化为0的结构,所以使用折叠结构必须选择2+4*n的阶数才可以用
,也就是选择8阶是不行的用不了IP核,所以我又重新换成10阶了,这样就省的的打代码了写滤波器了(我比较懒)。
第三个问题
如果你使用希尔伯特滤波器生成两路正交的的信号,且要求最后幅值近似相同,这可以通过matlab仿真判断,
但是fpga是定点数计算,所以你必须确定好定点小数的小数点位置的位宽才可以满足在数字里面幅值相同。
在我看来有两种办法。
-
第一种,通过量化后的系数代入matlab仿真看看幅值背倍数的关系,确定好倍数,然后在fpga除去。其中最好是把倍数控制为2
n
这样会很方便。所以以上杜勇老师代码需要微调一下,这样就可近似达到我们想要的效果,这个通过仿真可以很方便达到。 -
第二种,找到倍数关系,不微调,通过除法分解的若干2
n
项逐次逼近,得到一个近似结果。显然,这种方法往往没有第一种准,而且需要手打代码,所以不建议。但图像处理中经常用到。
采用第一种测试方法,发现在全部采用0定点小数位时,扩大倍数为

找到最近的为2048 ,2的11次幂,所以原先量化数据集体除以 3.4283e+03 /2048 =1.6740;
最后的10阶滤波器的fix12_0量化值为

-210 0 357 0 -1223 0 1223 0 357 0 210
fpga仿真
临时有事要做,国庆再弄,未完待续,就剩实际一个仿真了
接着上面的:
0. matlab 量化后仿真结果
%数据分帧
FS=fs;
N=0.2*FS %帧长度 1M 约为0.2s
l=length(c1); %数据长度
f=fix(l/N) ; %帧数
ch1=c1(1:f*N); %数据取整
c1=reshape(ch1,[N,f]); %数据重排 每列即为一帧数据
%求均值
ch1_average = sum(c1)/N;
ch1_average_r = repmat(ch1_average,N,1);
c1 = c1 - ch1_average_r;
%希尔伯特变换得出C2,c1延迟25拍
c2=filter(Num,1,c1); %fpga 实现 51阶数, C1延迟25拍和c2进行计算,且水平偏移可以忽略不计
load('h_pm12.mat');
h_pm12_s = h_pm12/1.6740;
c3=filter(h_pm12_s,1,c1);
c3 = c3/2048;
plot(c1(:,2),'r');hold on;plot(c2(:,2),'b');hold on;plot(c3(:,2),'y');
legend('原始数据','希尔伯特浮点变换','12bit量化后');
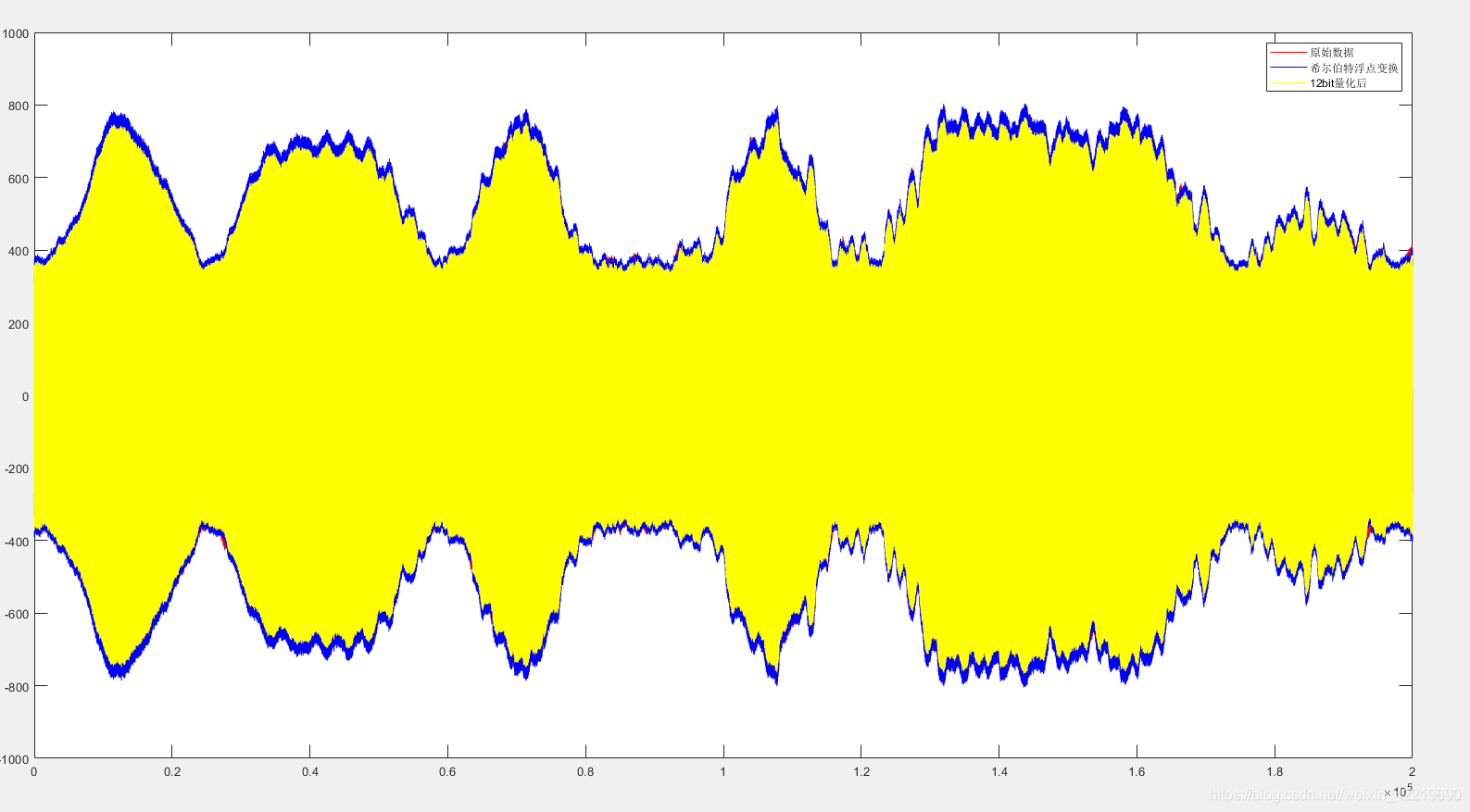
可以看到,处理过后幅值几乎一样,处理后的数据幅值几乎一样没什么区别
1.原始数据导出;
matlab代码如下
Fs=1e6; %采样频率为2KHz
N=16; %输入数据量化位数
%产生信号
fid = fopen('data_0_ch1.dat');
c1=fread(fid,Inf,'float');
fclose(fid);
%归一化处理
s=c1/2^15;
%16比特量化
Q_s=round(s*(2^(N-1)-1));
fid=fopen('C:\Users\window\Desktop\希尔伯特变换任务\s_data1_16.txt','w');
for i=1:length(Q_s)
B_s=dec2bin(Q_s(i)+(Q_s(i)<0)*2^N,N);
for j=1:N
if B_s(j)=='1'
tb=1;
else
tb=0;
end
fprintf(fid,'%d',tb);
end
fprintf(fid,'\r\n');
end
fprintf(fid,';');
fclose(fid);
fpga仿真文件
`timescale 1ns / 1ps
//
// Company:
// Engineer:
//
// Create Date: 2019/10/08 10:30:20
// Design Name:
// Module Name: test_hilbert10
// Project Name:
// Target Devices:
// Tool Versions:
// Description:
//
// Dependencies:
//
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
//
//
module test_hilbert10(
//验证模块
);
reg clk;
reg rst_n;
reg s_axis_tvalid=0;
reg [15:0] data;
parameter clk_period=1000;
parameter clk_half_period=clk_period/2;
parameter data_num=100000;
parameter time_sim=data_num*clk_period/2;
parameter data_period=clk_period;
integer Pattern0;
reg [15:0] stimulus0[1:data_num];
initial
begin
clk =0;
rst_n = 0;
Pattern0=0;
#10000 rst_n = 1; //ip核要保证许多时钟周期后复位
$readmemb("E:/FPGA_project/test_CSDN/s_data1_16.txt",stimulus0);
repeat(data_num)
begin
Pattern0=Pattern0+1;
data=stimulus0[Pattern0];
//#data_period;
@(negedge clk);
end
end
always
# clk_half_period clk = ~clk;
always @ (posedge clk)
begin
if(!rst_n)
begin
s_axis_tvalid <= 0;
end
else
begin
if(data_num >= 10)
begin
s_axis_tvalid <=1;
end
end
end
wire [39:0] m_axis_data_tdata;
wire [15:0] real_data;
wire [16:0] imag_data;
wire m_axis_data_tvalid;
wire s_axis_data_tready;
hibert_10 your_instance_name (
.aclk(clk), // input wire aclk
.s_axis_data_tvalid(s_axis_tvalid), // input wire s_axis_data_tvalid
.s_axis_data_tready(s_axis_data_tready), // output wire s_axis_data_tready
.s_axis_data_tdata(data), // input wire [15 : 0] s_axis_data_tdata
.m_axis_data_tvalid(m_axis_data_tvalid), // output wire m_axis_data_tvalid
.m_axis_data_tdata(m_axis_data_tdata) // output wire [39 : 0] m_axis_data_tdata
);
assign real_data = m_axis_data_tdata[15:0];
assign imag_data = {m_axis_data_tdata[32],m_axis_data_tdata[30:16]};
endmodule
仿真结果

注意的问题
- 根据希尔伯特滤波器的频率响应可知,其对直流分量有极大的抑制作用,fpga仿真也支持这一个结果,在原始信号中添加直流分量,最后结果也被消除了。所以如果信号含有较大直流分量,一定要先帧均值化,在希尔伯特正交两路,才能保证幅值相似。
- 最后两路输出幅值还是有1-5%的误差,这个问题一个是原始测试数据量化导致的,一个是ip核滤波器设置导致的,一般不会影响处理,建议把两路数据读出来,带进matlabf仿真中处理
// 打开文件
integer A;
integer B;
initial
begin
A=$fopen("E:/FPGA_project/test_CSDN/A.txt","w");
B=$fopen("E:/FPGA_project/test_CSDN/B.txt","w");
end
//写入10进制按无符号数写入 , 在matlab 中变为有符号数计算
always @(posedge clk)
begin
if(m_axis_data_tvalid)
begin
$fdisplay(A,"%d",real_data );
$fdisplay(B,"%d",imag_data );
end
end
//matlab 无符号数变有符号数
A =load('A.txt');
B =load('B.txt');
for i=1:length(A)
if(A(i) >= 2^(15))
A(i) = A(i) - 2^(16);
else
A(i) = A(i);
end
if(B(i) >= 2^(15))
B(i) = B(i) - 2^(16);
else
B(i) = B(i);
end
end

经过测试,fpga仿真的输出数据满足了后续算法的需求,整体仿真通过,希尔伯特模块完成任务。
ip配置图如下: