文章目录
参考资料
-
自动驾驶中的规划控制概述
-
A Survey of Motion Planning and Control Techniques for Self-Driving Urban Vehicles
-
https://zhuanlan.zhihu.com/p/46377932
-
pythonRobotics
-
Frenet坐标推导过程整理
-
Frenet坐标系相关知识系统学习
-
后轮位置反馈
-
后轴反馈控制——frenet坐标的一个应用
1. 基本概念
后轮反馈控制(Rear wheel feedback)是利用
后轮中心的跟踪偏差
来进行转向控制量计算的方法。
如图所示,参考轨迹上与车辆后轴中心距离最近的点
(
x
r
e
f
,
y
r
e
f
)
(x_{ref},y_{ref})
(
x
r
e
f
,
y
r
e
f
)
为:
s
(
t
)
=
arg
min
γ
∥
(
x
r
(
t
)
,
y
r
(
t
)
)
−
(
x
r
e
f
(
γ
)
,
y
r
e
f
(
γ
)
)
∥
(1)
\tag{1} s(t)=\arg \min _{\gamma}\left\|\left(x_{r}(t), y_{r}(t)\right)-\left(x_{r e f}(\gamma), y_{r e f}(\gamma)\right)\right\|
s
(
t
)
=
ar
g
γ
min
∥
(
x
r
(
t
)
,
y
r
(
t
)
)
−
(
x
r
e
f
(
γ
)
,
y
r
e
f
(
γ
)
)
∥
(
1
)
其中,
(
x
r
(
t
)
,
y
r
(
t
)
)
\left(x_{r}(t), y_{r}(t)\right)
(
x
r
(
t
)
,
y
r
(
t
)
)
代表
t
t
t
时刻车辆后轴中心位置坐标,
(
x
r
e
f
(
γ
)
,
y
r
e
f
(
γ
)
)
\left(x_{r e f}(\gamma), y_{r e f}(\gamma)\right)
(
x
r
e
f
(
γ
)
,
y
r
e
f
(
γ
)
)
代表参考路径上离车辆后 轴距离最近点的位置坐标,
s
(
t
)
s(t)
s
(
t
)
代表
t
t
t
时刻与车辆后轴中心点距离最近参考轨迹点的位置参数
γ
\gamma
γ
。
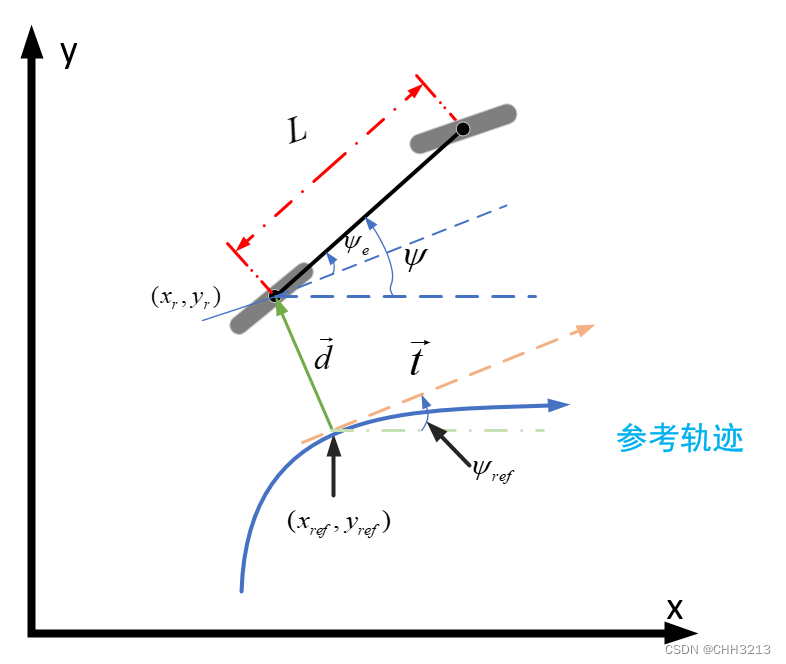
参考路径在
s
(
t
)
s(t)
s
(
t
)
参数处的单位切向量为
t
⃗
=
(
∂
x
r
e
f
∂
s
∥
s
(
t
)
,
∂
y
r
e
f
∂
s
∥
s
(
t
)
)
∥
(
∂
x
r
e
f
(
s
(
t
)
)
∂
s
,
∂
y
r
e
f
(
s
(
t
)
)
∂
s
)
∥
=
(
t
x
,
t
y
)
(2)
\tag{2} \vec{t}=\frac{\left(\frac{\partial x_{r e f}}{\partial s}\left\|_{s(t)}, \frac{\partial y_{r e f}}{\partial s}\right\|_{s(t)}\right)}{\left\|\left(\frac{\partial x_{r e f}(s(t))}{\partial s}, \frac{\partial y_{r e f}(s(t))}{\partial s}\right)\right\|}=\left(t_{x}, t_{y}\right)
t
=
∥
∥
∥
(
∂
s
∂
x
r
e
f
(
s
(
t
)
)
,
∂
s
∂
y
r
e
f
(
s
(
t
)
)
)
∥
∥
∥
(
∂
s
∂
x
r
e
f
∥
∥
∥
s
(
t
)
,
∂
s
∂
y
r
e
f
∥
∥
∥
s
(
t
)
)
=
(
t
x
,
t
y
)
(
2
)
跟踪误差向量表示如下:
d
⃗
(
t
)
=
(
x
r
(
t
)
−
x
r
e
f
(
s
(
t
)
)
,
y
r
(
t
)
−
y
r
e
f
(
s
(
t
)
)
)
=
(
d
x
,
d
y
)
(3)
\tag{3} \vec{d}(t)=\left(x_{r}(t)-x_{r e f}(s(t)), y_{r}(t)-y_{r e f}(s(t))\right)=\left(d_{x}, d_{y}\right)
d
(
t
)
=
(
x
r
(
t
)
−
x
r
e
f
(
s
(
t
)
)
,
y
r
(
t
)
−
y
r
e
f
(
s
(
t
)
)
)
=
(
d
x
,
d
y
)
(
3
)
所以跟踪误差向量
d
⃗
\vec{d}
d
和参考路径上最近点的单位切向量
t
⃗
\vec{t}
t
的叉积为
e
⃗
=
t
⃗
×
d
⃗
=
∣
t
x
t
y
d
x
d
y
∣
=
t
x
d
y
−
t
y
d
x
(4)
\tag{4} \vec{e}=\vec{t} \times \vec{d}=\left|\begin{array}{cc} t_{x} & t_{y} \\ d_{x} & d_{y} \end{array}\right|=t_{x} d_{y}-t_{y} d_{x}
e
=
t
×
d
=
∣
∣
∣
∣
t
x
d
x
t
y
d
y
∣
∣
∣
∣
=
t
x
d
y
−
t
y
d
x
(
4
)
关于车辆航向向量与目标路径切向量的夹角
ψ
e
\psi_{e}
ψ
e
如下:
ψ
e
(
t
)
=
ψ
−
arctan
∂
y
r
e
f
(
s
(
t
)
)
/
∂
s
∂
x
r
e
f
(
s
(
t
)
)
/
∂
s
(5)
\tag{5} \psi_{e}(t)=\psi-\arctan \frac{\partial y_{r e f}(s(t))/\partial s} {\partial x_{r e f}(s(t))/\partial s}
ψ
e
(
t
)
=
ψ
−
arctan
∂
x
r
e
f
(
s
(
t
)
)
/
∂
s
∂
y
r
e
f
(
s
(
t
)
)
/
∂
s
(
5
)
根据上图,
ψ
e
\psi_{e}
ψ
e
还可以表示如下:
ψ
e
(
t
)
=
ψ
−
ψ
r
e
f
(6)
\tag{6} \psi_{e}(t)=\psi-\psi_{ref}
ψ
e
(
t
)
=
ψ
−
ψ
r
e
f
(
6
)
如上图所示,车辆沿目标路径顺时针运动,在参考路径左侧,此时
e
>
0
e>0
e
>
0
。当在参考路径右侧时,
e
<
0
e<0
e
<
0
.
s
˙
\dot{s}
s
˙
可以表示为:
s
˙
=
v
r
⋅
cos
(
ψ
e
)
1
−
k
(
s
)
e
(8)
\tag{8} \dot{s}=\frac{v_{r} \cdot \cos \left(\psi_{e}\right)}{1-k(s) e}
s
˙
=
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
(
8
)
其中
k
(
s
)
k(s)
k
(
s
)
表示曲线在参考点s处的曲率,
v
r
v_r
v
r
表示后轮线速度。
车辆横向移动的速度
e
˙
\dot{e}
e
˙
可以表示如下:
e
˙
=
v
r
⋅
sin
(
ψ
e
)
(9)
\tag{9} \dot{e}=v_{r} \cdot \sin \left(\psi_{e}\right)
e
˙
=
v
r
⋅
sin
(
ψ
e
)
(
9
)
关于车辆航向角误差的变化率表示如下:
ψ
˙
e
=
ψ
˙
−
ψ
˙
r
e
f
=
ψ
˙
−
s
˙
⋅
k
(
s
)
=
ψ
˙
−
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
1
−
k
(
s
)
e
(10)
\tag{10} \begin{aligned} \dot{\psi}_{e} &=\dot{\psi}-\dot{\psi}_{r e f} \\ &=\dot{\psi}-\dot{s} \cdot k(s) \\ &=\dot{\psi}-\frac{v_{r} \cdot \cos \left(\psi_{e}\right) \cdot k(s)}{1-k(s) e} \end{aligned}
ψ
˙
e
=
ψ
˙
−
ψ
˙
r
e
f
=
ψ
˙
−
s
˙
⋅
k
(
s
)
=
ψ
˙
−
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
(
1
0
)
综上所述,基于上述参考曲线处的速度、横向误差变化率和航向角误差变化率如下:
s
˙
=
v
r
⋅
cos
(
ψ
e
)
1
−
k
(
s
)
e
e
˙
=
v
r
⋅
sin
(
ψ
e
)
ψ
˙
e
=
ψ
˙
−
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
1
−
k
(
s
)
e
(11)
\tag{11} \begin{aligned} \dot{s} &=\frac{v_{r} \cdot \cos \left(\psi_{e}\right)}{1-k(s) e} \\ \dot{e} &=v_{r} \cdot \sin \left(\psi_{e}\right) \\ \dot{\psi}_{e} &=\dot{\psi}-\frac{v_{r} \cdot \cos \left(\psi_{e}\right) \cdot k(s)}{1-k(s) e} \end{aligned}
s
˙
e
˙
ψ
˙
e
=
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
=
v
r
⋅
sin
(
ψ
e
)
=
ψ
˙
−
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
(
1
1
)
其实公式(11)这就是
Frenet
坐标系下的公式。有关
Frenet
坐标系参考
这篇博客
。
Frenet
坐标系使用道路的中心线作为参考线,使用参考线的 切线向量 和 法线向量 建立坐标系,那么基于参考线的位置就可以使用 纵向距离 和 横向距离 来描述任意位置;同时纵向和横向的速度、加速度、加加速度等信息也更便于计算
笛卡尔坐标系与Frenet坐标系对比如下:
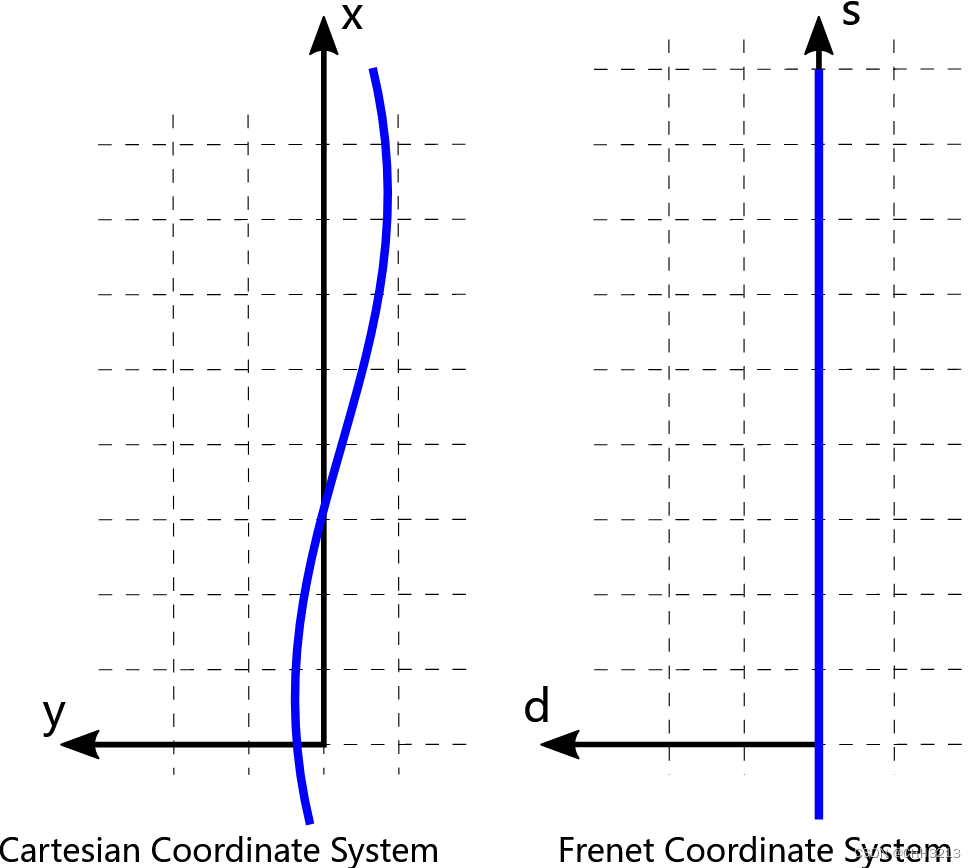
2. 李雅普诺夫稳定判据
基于上述微分方程,采用
李雅普诺夫第二方法
,寻找一个状态量的方程
V
(
x
)
V(x)
V
(
x
)
,也就是
V
(
e
,
ψ
e
)
V(e,\psi_e)
V
(
e
,
ψ
e
)
,定义李雅普诺夫函数形式如下:
V
(
e
,
ψ
e
)
=
1
2
e
2
+
1
2
k
2
ψ
e
2
(12)
\tag{12} V\left(e, \psi_{e}\right)=\frac{1}{2} e^{2}+\frac{1}{2 k_{2}} \psi_{e}^{2}
V
(
e
,
ψ
e
)
=
2
1
e
2
+
2
k
2
1
ψ
e
2
(
1
2
)
其中 参数
k
2
>
0
k_{2}>0
k
2
>
0
,为了使
(
e
,
ψ
e
)
\left(e, \psi_{e}\right)
(
e
,
ψ
e
)
在平衡点
(
0
,
0
)
(0,0)
(
0
,
0
)
处稳定,根据李雅普诺夫稳定判据,必须满足以下两个条 件:
-
lim
∣
e
,
ψ
e
∣
→
∞
V
=
∞
\lim _{\left|e, \psi_{e}\right| \rightarrow \infty} V=\infty
lim
∣
e
,
ψ
e
∣
→
∞
V
=
∞
-
V˙
<
0
(
e
≠
0
,
ψ
e
≠
0
)
\dot{V}<0 \quad\left(e \neq 0, \psi_{e} \neq 0\right)
V
˙
<
0
(
e
=
0
,
ψ
e
=
0
)
对于条件1,等式(12)明显成立,所以李雅普诺夫稳定判据第一条满足。
对于
V
˙
\dot{V}
V
˙
,结合等式(11)的微分方程,推导形式如下:
V
˙
=
e
e
˙
+
1
k
2
ψ
e
ψ
˙
e
=
e
⋅
v
r
⋅
sin
(
ψ
e
)
+
1
k
2
ψ
e
(
ψ
˙
−
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
1
−
k
(
s
)
e
)
(13)
\tag{13} \begin{aligned} \dot{V} &=e \dot{e}+\frac{1}{k_{2}} \psi_{e} \dot{\psi}_{e} \\ &=e \cdot v_{r} \cdot \sin \left(\psi_{e}\right)+\frac{1}{k_{2}} \psi_{e}\left(\dot{\psi}-\frac{v_{r} \cdot \cos \left(\psi_{e}\right) \cdot k(s)}{1-k(s) e}\right) \end{aligned}
V
˙
=
e
e
˙
+
k
2
1
ψ
e
ψ
˙
e
=
e
⋅
v
r
⋅
sin
(
ψ
e
)
+
k
2
1
ψ
e
(
ψ
˙
−
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
)
(
1
3
)
我们需要做的就是设计一个
ψ
˙
\dot{\psi}
ψ
˙
,使得
V
˙
<
0
\dot{V}<0
V
˙
<
0
即满足第2条李雅普诺夫稳定判据。
根据等式(13),令
V
˙
=
0
\dot{V}=0
V
˙
=
0
,化简得
k
2
v
r
sin
(
ψ
e
)
ψ
e
e
+
ψ
˙
−
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
1
−
k
(
s
)
e
=
0
(14)
\tag{14} k_{2} v_{r} \frac{\sin \left(\psi_{e}\right)}{\psi_{e}} e+\dot{\psi}-\frac{v_{r} \cdot \cos \left(\psi_{e}\right) \cdot k(s)}{1-k(s) e}=0
k
2
v
r
ψ
e
sin
(
ψ
e
)
e
+
ψ
˙
−
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
=
0
(
1
4
)
故临界控制率
ψ
˙
∗
\dot{\psi}^{*}
ψ
˙
∗
为:
ψ
˙
∗
=
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
1
−
k
(
s
)
e
−
k
2
v
r
sin
(
ψ
e
)
ψ
e
e
(15)
\tag{15} \dot{\psi}^{*}=\frac{v_{r} \cdot \cos \left(\psi_{e}\right) \cdot k(s)}{1-k(s) e}-k_{2} v_{r} \frac{\sin \left(\psi_{e}\right)}{\psi_{e}} e
ψ
˙
∗
=
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
−
k
2
v
r
ψ
e
sin
(
ψ
e
)
e
(
1
5
)
为了满足第2条李雅普诺夫稳定判据,设置一个调节函数
g
(
e
,
ψ
e
,
t
)
>
0
g\left(e, \psi_{e}, t\right)>0
g
(
e
,
ψ
e
,
t
)
>
0
,可以得出基于航向角变化率的控 制命令:
ψ
˙
=
ψ
˙
∗
−
g
(
e
,
ψ
e
,
t
)
ψ
e
(16)
\tag{16} \dot{\psi}=\dot{\psi}^{*}-g\left(e, \psi_{e}, t\right) \psi_{e}
ψ
˙
=
ψ
˙
∗
−
g
(
e
,
ψ
e
,
t
)
ψ
e
(
1
6
)
设
g
(
e
,
ψ
e
,
t
)
=
k
ψ
∣
v
r
∣
g\left(e, \psi_{e}, t\right)=k_{\psi}\left|v_{r}\right|
g
(
e
,
ψ
e
,
t
)
=
k
ψ
∣
v
r
∣
,其中
k
ψ
>
0
k_{\psi}>0
k
ψ
>
0
。
ψ
˙
=
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
1
−
k
(
s
)
e
−
k
2
v
r
sin
(
ψ
e
)
ψ
e
e
−
k
ψ
∣
v
r
∣
ψ
e
(17)
\tag{17} \dot{\psi}=\frac{v_{r} \cdot \cos \left(\psi_{e}\right) \cdot k(s)}{1-k(s) e}-k_{2} v_{r} \frac{\sin \left(\psi_{e}\right)}{\psi_{e}} e-k_{\psi}\left|v_{r}\right| \psi_{e}
ψ
˙
=
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
−
k
2
v
r
ψ
e
sin
(
ψ
e
)
e
−
k
ψ
∣
v
r
∣
ψ
e
(
1
7
)
将等式(17)带入等式(13)得
V
˙
=
v
r
⋅
sin
(
ψ
e
)
⋅
e
+
1
k
2
ψ
e
(
ψ
˙
−
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
1
−
k
(
s
)
e
)
=
v
r
⋅
sin
(
ψ
e
)
⋅
e
+
1
k
2
ψ
e
(
−
k
2
v
r
sin
(
ψ
e
)
ψ
e
e
−
k
ψ
∣
v
r
∣
ψ
e
)
=
v
r
⋅
sin
(
ψ
e
)
⋅
e
−
v
r
⋅
sin
(
ψ
e
)
⋅
e
−
k
ψ
k
2
∣
v
r
∣
ψ
e
2
=
−
k
ψ
k
2
∣
v
r
∣
ψ
e
2
≤
0
(18)
\tag{18} \begin{aligned} \dot{V} &=v_{r} \cdot \sin \left(\psi_{e}\right) \cdot e+\frac{1}{k_{2}} \psi_{e}\left(\dot{\psi}-\frac{v_{r} \cdot \cos \left(\psi_{e}\right) \cdot k(s)}{1-k(s) e}\right) \\ &=v_{r} \cdot \sin \left(\psi_{e}\right) \cdot e+\frac{1}{k_{2}} \psi_{e}\left(-k_{2} v_{r} \frac{\sin \left(\psi_{e}\right)}{\psi_{e}} e-k_{\psi}\left|v_{r}\right| \psi_{e}\right) \\ &=v_{r} \cdot \sin \left(\psi_{e}\right) \cdot e-v_{r} \cdot \sin \left(\psi_{e}\right) \cdot e-\frac{k_{\psi}}{k_{2}}\left|v_{r}\right| \psi_{e}^{2} \\ &=-\frac{k_{\psi}}{k_{2}}\left|v_{r}\right| \psi_{e}^{2} \leq 0 \end{aligned}
V
˙
=
v
r
⋅
sin
(
ψ
e
)
⋅
e
+
k
2
1
ψ
e
(
ψ
˙
−
1
−
k
(
s
)
e
v
r
⋅
cos
(
ψ
e
)
⋅
k
(
s
)
)
=
v
r
⋅
sin
(
ψ
e
)
⋅
e
+
k
2
1
ψ
e
(
−
k
2
v
r
ψ
e
sin
(
ψ
e
)
e
−
k
ψ
∣
v
r
∣
ψ
e
)
=
v
r
⋅
sin
(
ψ
e
)
⋅
e
−
v
r
⋅
sin
(
ψ
e
)
⋅
e
−
k
2
k
ψ
∣
v
r
∣
ψ
e
2
=
−
k
2
k
ψ
∣
v
r
∣
ψ
e
2
≤
0
(
1
8
)
所以设计的控制率满足稳定性条件。
注意,可以选择另外的李雅普诺夫函数然后重新设计控制率,只要设计的李雅普诺夫函数能够满足稳定性判据即可。
根据车辆几何关系
tan
(
δ
)
=
L
R
(19)
\tag{19} \tan (\delta)=\frac{L}{R}
tan
(
δ
)
=
R
L
(
1
9
)
车辆航向变化率与车速和转弯半径的关系为
ψ
˙
=
v
R
\dot{\psi}=\frac{v}{R}
ψ
˙
=
R
v
,结合等式
(
17
)
(17)
(
1
7
)
可得
tan
(
δ
)
=
ψ
˙
L
v
(20)
\tag{20} \tan (\delta)=\frac{\dot{\psi} L}{v}
tan
(
δ
)
=
v
ψ
˙
L
(
2
0
)
所以控制率
δ
\delta
δ
为
δ
=
arctan
(
ψ
˙
L
v
r
)
(21)
\tag{21} \delta=\arctan \left(\frac{\dot{\psi} L}{v_{r}}\right)
δ
=
arctan
(
v
r
ψ
˙
L
)
(
2
1
)
3. python代码实现
3.1 车辆模型
设
车辆运动学模型
为
以后轴中心为车辆中心的单车运动学模型
(具体可参考笔者之前的
博客
),即
{
x
˙
=
V
cos
(
ψ
)
y
˙
=
V
sin
(
ψ
)
ψ
˙
=
V
L
tan
δ
f
V
˙
=
a
\left\{\begin{array}{l} \dot{x}=V \cos (\psi) \\ \dot{y}=V \sin (\psi) \\ \dot{\psi}=\frac{V}{L}\tan{\delta_f}\\ \dot{V}=a \end{array}\right.
⎩
⎪
⎪
⎨
⎪
⎪
⎧
x
˙
=
V
cos
(
ψ
)
y
˙
=
V
sin
(
ψ
)
ψ
˙
=
L
V
tan
δ
f
V
˙
=
a
python实现代码如下。
import math
class KinematicModel_3:
"""假设控制量为转向角delta_f和加速度a
"""
def __init__(self, x, y, psi, v, L, dt):
self.x = x
self.y = y
self.psi = psi
self.v = v
self.L = L
# 实现是离散的模型
self.dt = dt
def update_state(self, a, delta_f):
self.x = self.x+self.v*math.cos(self.psi)*self.dt
self.y = self.y+self.v*math.sin(self.psi)*self.dt
self.psi = self.psi+self.v/self.L*math.tan(delta_f)*self.dt
self.v = self.v+a*self.dt
def get_state(self):
return self.x, self.y, self.psi, self.v
3.2 相关参数设置
K_psi=1.0
K2=0.5 #李雅普诺夫的参数
dt=0.1 # 时间间隔,单位:s
L=2 # 车辆轴距,单位:m
v = 2 # 初始速度
x_0=0 # 初始x
y_0=0 #初始y
psi_0=0 # 初始航向角
3.3 生成轨迹曲线
class MyReferencePath:
def __init__(self):
# set reference trajectory
# refer_path包括4维:位置x, 位置y, 轨迹点的切线方向, 曲率k
self.refer_path = np.zeros((1000, 4))
self.refer_path[:,0] = np.linspace(0, 100, 1000) # x
self.refer_path[:,1] = 2*np.sin(self.refer_path[:,0]/3.0)+2.5*np.cos(self.refer_path[:,0]/2.0) # y
# 使用差分的方式计算路径点的一阶导和二阶导,从而得到切线方向和曲率
for i in range(len(self.refer_path)):
if i == 0:
dx = self.refer_path[i+1,0] - self.refer_path[i,0]
dy = self.refer_path[i+1,1] - self.refer_path[i,1]
ddx = self.refer_path[2,0] + self.refer_path[0,0] - 2*self.refer_path[1,0]
ddy = self.refer_path[2,1] + self.refer_path[0,1] - 2*self.refer_path[1,1]
elif i == (len(self.refer_path)-1):
dx = self.refer_path[i,0] - self.refer_path[i-1,0]
dy = self.refer_path[i,1] - self.refer_path[i-1,1]
ddx = self.refer_path[i,0] + self.refer_path[i-2,0] - 2*self.refer_path[i-1,0]
ddy = self.refer_path[i,1] + self.refer_path[i-2,1] - 2*self.refer_path[i-1,1]
else:
dx = self.refer_path[i+1,0] - self.refer_path[i,0]
dy = self.refer_path[i+1,1] - self.refer_path[i,1]
ddx = self.refer_path[i+1,0] + self.refer_path[i-1,0] - 2*self.refer_path[i,0]
ddy = self.refer_path[i+1,1] + self.refer_path[i-1,1] - 2*self.refer_path[i,1]
self.refer_path[i,2]=math.atan2(dy,dx) # yaw
# 计算曲率:设曲线r(t) =(x(t),y(t)),则曲率k=(x'y" - x"y')/((x')^2 + (y')^2)^(3/2).
# 参考:https://blog.csdn.net/weixin_46627433/article/details/123403726
self.refer_path[i,3]=(ddy * dx - ddx * dy) / ((dx ** 2 + dy ** 2)**(3 / 2)) # 曲率k计算
def calc_track_error(self, x, y):
"""计算跟踪误差
Args:
x (_type_): 当前车辆的位置x
y (_type_): 当前车辆的位置y
Returns:
_type_: _description_
"""
d_x = [self.refer_path[i,0]-x for i in range(len(self.refer_path))]
d_y = [self.refer_path[i,1]-y for i in range(len(self.refer_path))]
d = [np.sqrt(d_x[i]**2+d_y[i]**2) for i in range(len(d_x))]
s = np.argmin(d)
yaw = self.refer_path[s, 2]
k = self.refer_path[s, 3]
angle = normalize_angle(yaw - math.atan2(d_y[s], d_x[s]))
e = d[s] # 误差
if angle < 0:
e *= -1
return e, k, yaw, s
3.4 角度归一化
def normalize_angle(angle):
"""
Normalize an angle to [-pi, pi].
:param angle: (float)
:return: (float) Angle in radian in [-pi, pi]
copied from https://atsushisakai.github.io/PythonRobotics/modules/path_tracking/stanley_control/stanley_control.html
"""
while angle > np.pi:
angle -= 2.0 * np.pi
while angle < -np.pi:
angle += 2.0 * np.pi
return angle
3.5 后轮反馈控制算法实现
def rear_wheel_feedback_control(robot_state, e, k, refer_path_psi):
"""后轮位置反馈控制
Args:
robot_state (_type_): 机器人位姿,包括x,y,yaw,v
e (_type_): _description_
k (_type_): 曲率
refer_path (_type_): 参考轨迹
refer_path_psi (_type_): 参考轨迹上点的切线方向的角度
Returns:
_type_: _description_
"""
psi,v = robot_state[2], robot_state[3]
psi_e = normalize_angle(psi - refer_path_psi)
# 公式17
psi_dot = v * k * math.cos(psi_e) / (1.0 - k * e) - K2 * v * math.sin(psi_e) * e / psi_e- K_psi * abs(v) * psi_e
if psi_e == 0.0 or psi_dot == 0.0:
return 0.0
# 公式21
delta = math.atan2(L * psi_dot, v)
return delta
3.6 主函数
from celluloid import Camera # 保存动图时用,pip install celluloid
def main_2():
print("rear wheel feedback tracking start!!")
reference_path = MyReferencePath()
goal = reference_path.refer_path[-1,0:2]
# 运动学模型
ugv = KinematicModel_3(x_0, y_0, psi_0, v, L, dt)
x_ = []
y_ = []
fig = plt.figure(1)
# 保存动图用
camera = Camera(fig)
# plt.ylim([-3,3])
for i in range(500):
robot_state = np.zeros(4)
robot_state[0] = ugv.x
robot_state[1] = ugv.y
robot_state[2]=ugv.psi
robot_state[3]=ugv.v
e, k, yaw_ref, s0 = reference_path.calc_track_error(robot_state[0], robot_state[1])
delta = rear_wheel_feedback_control(robot_state, e, k, yaw_ref)
ugv.update_state(0, delta) # 加速度设为0,恒速
x_.append(ugv.x)
y_.append(ugv.y)
# 显示动图
plt.cla()
plt.plot(reference_path.refer_path[:,0], reference_path.refer_path[:,1], "-.b", linewidth=1.0, label="course")
plt.plot(x_, y_, "-r", label="trajectory")
plt.plot(reference_path.refer_path[s0,0], reference_path.refer_path[s0,1], "go", label="target")
# plt.axis("equal")
plt.grid(True)
plt.pause(0.001)
# camera.snap()
# 判断是否到达最后一个点
if np.linalg.norm(robot_state[0:2]-goal)<=0.1:
print("reach goal")
break
# animation = camera.animate()
# animation.save('trajectory.gif')
main_2()
跟踪效果如下:

可见,跟踪效果非常好。
完整python代码文件见
github仓库
4. c++代码实现
由于在自动驾驶中算法实现一般使用C++,所以我也使用C++实现了相关功能,代码结构与python代码实现类似,这边就不再做相关代码解释了。完整代码详见另一个
github仓库
。