1. 二分法

二分查找是一个时间效率极高的算法，尤其是面对大量的数据时，其查找效率是极高，时间复杂度是log(n)。

主要思想就是不断的对半折叠，每次查找都能除去一半的数据量，直到最后将所有不符合条件的结果都去除，只剩下一个符合条件的结果。

2. 时间复杂度：

二分法的时间复杂度是log(n)，但log(n)为什么效率这么高呢？接下来我举个例子来描述一下：

我们都听说过指数爆炸，何为指数爆炸，就是在指数不断增加的情况下，其数值的上升速度不断增加，上升速率可以迅速的接近增无穷。

如图：

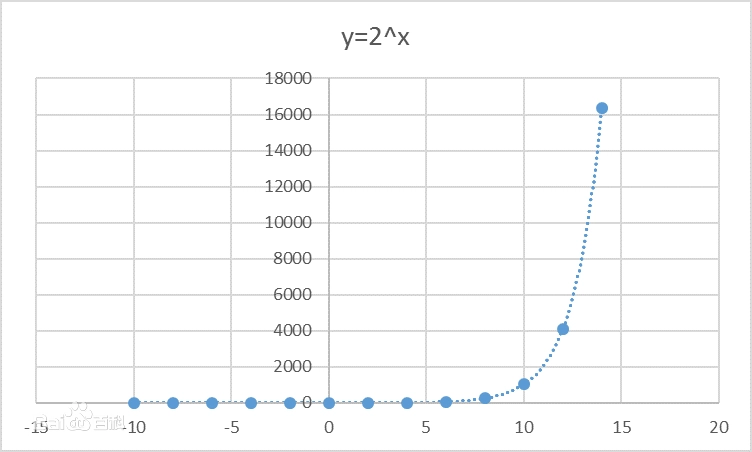
同样也有这样一个理论去描述指数爆炸的威力：那就是一个乒乓球每秒钟翻一倍，五分钟可以填满整个宇宙。

而我们二分法就相当于上升的逆转，一个每秒钟翻一倍的乒乓球，五分钟就可以堆满整个宇宙，反之，堆满整个宇宙的乒乓球，每秒钟减少一半，五分钟后就只剩一个。

3. 二分法的套路

使用二分法，我们要按照一下两个步骤：

1. 我们要确定一个区间[L，R]
2. 我们要找到一个性质，并且该性质满足一下两点：
   
   ①满足二段性
   
   ②答案是二段性的分界点。

这里可能很多人有疑问了，这性质到底是什么性质，其实就是根据题目找出的判断条件。

例如：

我们要在一组升序的数组找一个数的下标，那我们肯定是先拿中间的与他进行比较，更具比较大小这个判断，其实就相当于是这个性质，且这个性质满足二段性，将大于和小于我们要查找的值分为两段，而我们的查找结果就是

分界点

。

3.1 整数的二分

情况一：


当ans属于左边界时，如图进行划分：



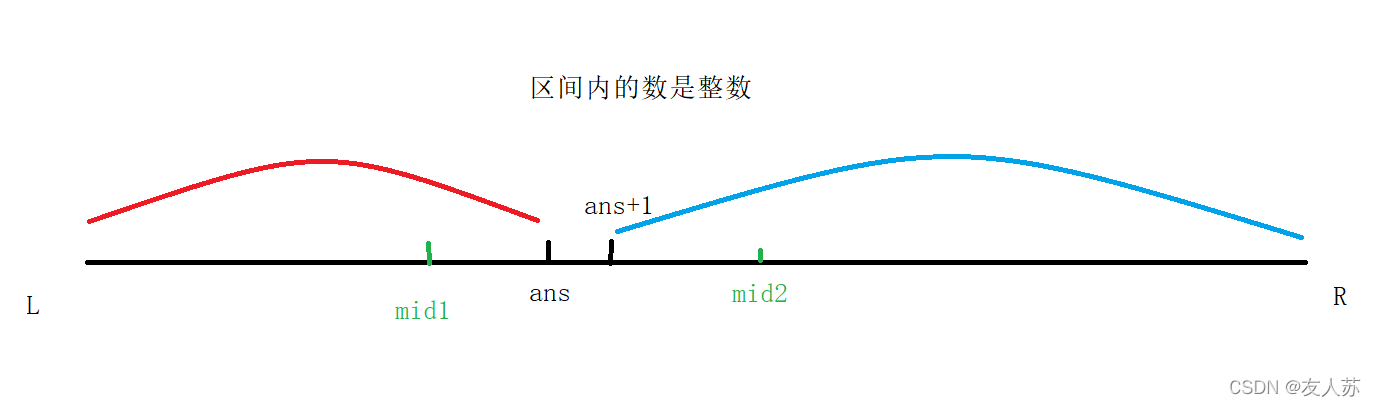
这种情况有两个区间[L，mid1]和[mid1 + 1，R]，我们要根据条件将某一半区间舍去，而为什么要这样划分呢？

根据图分析：

1. 当mid属于红色区域时，也就是mid1，我们发现，mid1是有可能等于ans的，为了避免我们将ans排除在区间外，我们令L = mid，从而在除去左边不需要的数据同时，好保证了ans任在区间内。
2. 当mid属于蓝色区域，及mid2时，mid2是不会等于ans的，所以我们可以将包括mid2的右边区间全部去除，及令R = mid – 1。

模板1如下：

while(l < r){
	int mid = l + r + 1 >> 2;//这里为什么要+1呢，请继续往下看
	if(在红色区域内)l = mid;
	else r = mid - 1;
}

我们取个临界情况，及当L = R – 1时，

我们知道，在上面这种情况下，是进行L = mid进行区间调整的，假设mid = (L + R) / 2，那么L = (L + R) / 2 = (2 * R – 1) / 2 = L(很明显的奇数除以二，会进行向下取整)，所以这样会造成死循环。

情况二：




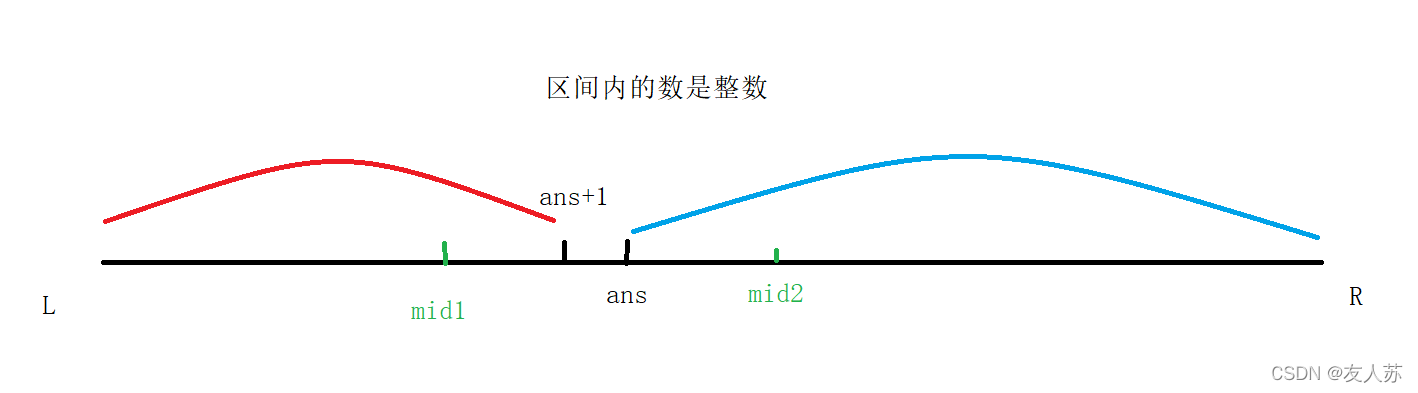
当ans属于右边界时：

这种情况划分为[L，mid – 1]和[mid，R]，因为当mid在蓝色区域(mid2)时，mid2可能等于ans。同样的分析方式，可以自己分析一下（加深理解）

模板2如下：

while(l < r){
	int mid = l + r >> 1;//左移1有除2的效果，+的优先级大于>>
	if(mid 属于蓝色区域) r = mid;
	else l = mid + 1;
}

3.2 实数的划分

实数的划分相对与整数要简单，没有这么多种情况，因为实数除以2的结果不会有什么向上或向下取整的情况，一定会有个原原本本的结果，就L = mid，R = mid这种区间转变的方式，而循环条件通常是L – R > 1e-6，1e的负次方根据题目进行调整。

模板：

while(l - r > 1e-6){
	if(arr[mid] > ans)l = mid;
	else r = mid;
}

四. 相关习题

实践才是检验整理的唯一标准，上面讲了这么多理论，刚开始接触的人可能还是会有点蒙，接下来我们看几个例子来真真切切的感受一下：

4.1 数的范围

题目链接：

789. 数的范围

这道题是一道模板题，并且我觉得很好，因为他把整数二分的两种模板都用上了。

题目要求：

题目要求是，给我们长度为n的升序数组和一个数q，q表示查询的次数，每次查询给一个值x，要求找出x的区间，比如1，2，2，3，4，4，4，如果x的4，那么我们的输出结果就是4 6，因为含有4的下标区间在[4，6]内。

思路分析：

1. 首先我们要获得判断确定区间，很明显区间是[0, n – 1]。
2. 寻找性质。
   
   我们先考虑如何寻找x的左边界，很明显处在左边界的值一定是>=x，
   
   如图：

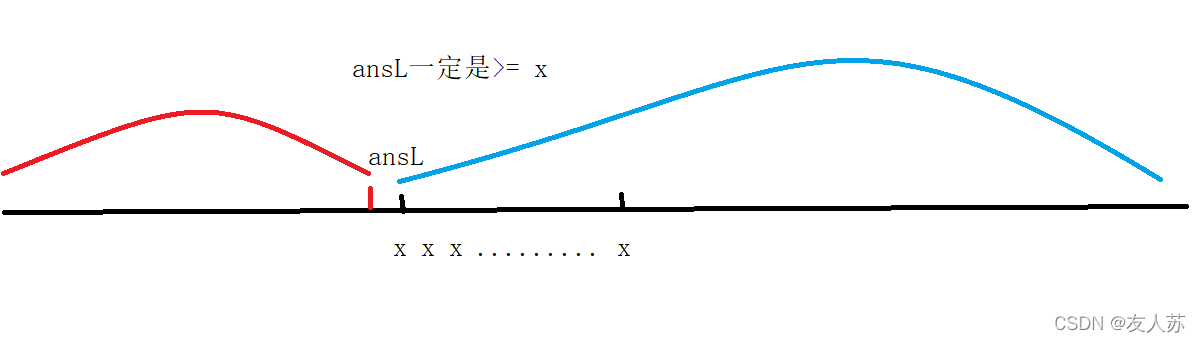
同时也刚好将区间分为两端，符合二段性，且是分界点。

我们继续分析：

因为ansL在蓝色范围内，所以我们应该进行如下转变方式：L = mid + 1，R = mid。

左边界代码如下：

while(l < r){
	int mid = l + r >> 1;
	if(a[mid] >= x)r = mid;
	else l = mid + 1;
}
//找出之后我们还要判断，a[r]是否等于x,如果不等于则说明没有x，输出-1 -1
if(a[r] != x)cout << "-1 -1" << endl;
else{//否则我们寻找r
	;
}

现在我们分析右边界


左边界是一定大于等于x，那么我们的右边界显然是判断小于等于x。



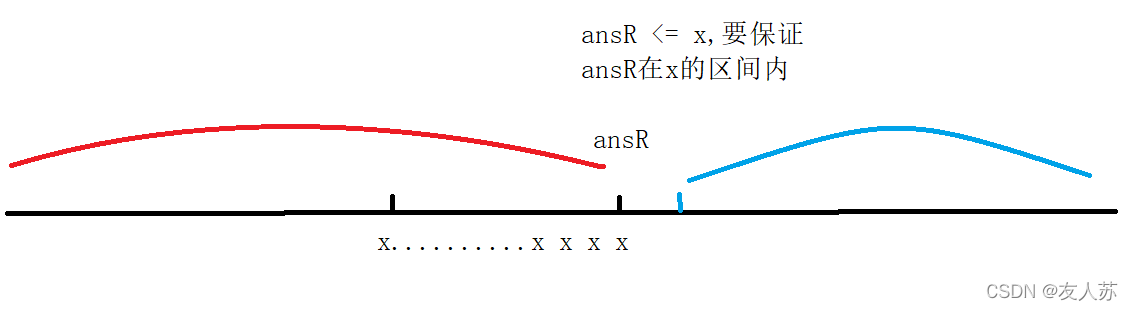
这时我们进行如下调换，L = mid，R = mid – 1，且mid = L + R + 1 >> 1。

右边界代码如下：

while(l < r){
	int mid = l + r + 1 >> 1;
	if(a[mid] <= x)l = mid;
	else r = mid - 1;
}

完整代码：

#include <cstdio>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, q;
int a[N];

int main(){
    cin >> n >> q;
    for(int i = 0; i < n; i++)scanf("%d", &a[i]);
    while(q -- ){
        int x;
        scanf("%d", &x);
        int l = 0, r = n - 1;
        //首先找到左区间的下标
        while(l < r){
            int mid = l + r >> 1;
            if(a[mid] >= x)r = mid;
            else l = mid + 1;
        }
        //判断a[l] == x
        if(a[r] != x)cout << "-1 -1" << endl;
        else {
            cout << l << ' ';//先将l输出
            r = n - 1;//重置r
            //查找ansL
            while(l < r){
                int mid = l + r + 1 >> 1;
                if(a[mid] <= x)l = mid;
                else r = mid - 1;
            }
            cout << r << endl;
        }
    }
    return 0;
}

4.2 数的三次方根

题目链接：


数的三次方根

题目分析：

这是一道实数二分的模板题，给定一个数，让我们求它的三次方根，精确到小数点后6位

思路分析：

首先题目给定的范围时-10000到10000，同时也是区间范围。

在这个区间范围内我们找一个数x，使得x * x * x等于n，则x就是n的三次方根，且x刚好是二段性的分界点，如果mid ^ 3>=n说明mid过大，则R = mid，否则L = mid。

循环条件：

R – L > 1e-8

为了保证精度够高，我们通常将范围缩小到比题目要求低二次方。

代码如下：

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;
int main(){
    double n;
    cin >> n;
    double l = -10000, r = 10000;
    while(r - l > 1e-8){
        double mid = (l + r) / 2;
        if(mid * mid * mid < n)l = mid;
        else r = mid;
    }
    printf("%.6lf\n", l);
    return 0;
}