博客

leetcode98.题目描述


给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

• 节点的左子树只包含小于当前节点的数。
• 节点的右子树只包含大于当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

解题思路：


1.错误思路

上来没看清题，用了这种解法，中间节点必须小于左孩子和大于右孩子，然后我们对每个子节点进行递归看成一个子问题，并返回True或者False，最后将底层节点逐步和上层节点相与，得到最后结果，这显然无法满足以下这种情况，但是还是能通过大多数案例的。

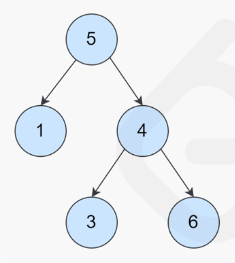
这里只对每个节点和它的左右孩子节点进行了判断，并没有对其所的子节点判断，比如图中右边的3节点就大于5，所以这种写法显然不合理。

2.中序遍历

很容发现二叉搜索树满足中序遍历有序，因为中间节点大于左边，小于右边，所以这很显然就是有序的，所以我们写出数的中序遍历，然后对中序遍历数组进行判断是否升序即可，代码如下

class Solution:
	#初始化数组来保存中序遍历结果
    def __init__(self):
        self.nums = []
    def isValidBST(self, root: TreeNode) -> bool:
		#中序遍历二叉树
        def mid_travel(root):
            if not root:
                return
            if root.left:
                mid_travel(root.left)
            self.nums.append(root.val)
            if root.right:
                mid_travel(root.right)
        #调用二叉树的中序遍历函数
        mid_travel(root)
        flag = True
        i = 1
        #判断数组是否为升序数组，如果不满足就flag改为False
        while i<len(self.nums):
            if self.nums[i-1]>=self.nums[i]:
                flag = False
                break
            i+=1
        return flag

3.递归法

其实这里的方法和我一中的错误方法类似，只不过我们需要改变一下判断条件，不应该只对每个节点判断其左右的孩子节点，要实现头结点是否满足条件，我们需要判断左边和右边所有的子节点是否满足条件。如果说从叶子节点开始判断起，从二叉树底部向顶部开始遍历这样显然不太现实，可以换一种思路，从顶部向底部开始判断，如果前面的节点确定了，我们可以推断出下面节点正确取值范围，如果不满足这个取值范围，就不是二叉搜索树，当然越向下取值范围越严格。盗用一张图说明一下。

class Solution:
    def isValidBST(self, root: TreeNode) -> bool:
        def _isValid(root,l = float('-inf'), r = float('inf')):
            if not root:
                return True
            if l<root.val<r:
               l_res = _isValid(root.left, l, root.val)
               r_res = _isValid(root.right, root.val, r)
               return l_res and r_res
            else:
                return False
        return _isValid(root)