博客

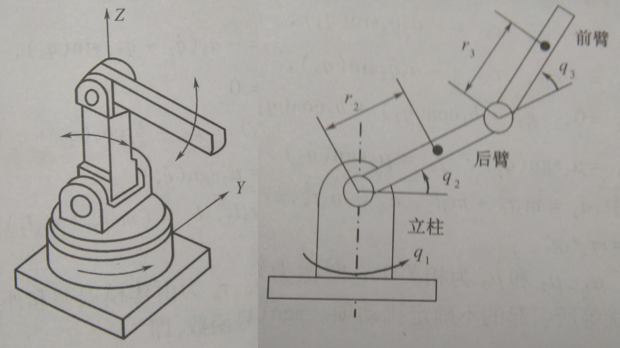
下图是三连杆机械臂，也就是常说的拟人臂。

采用拉格朗日方法并做适当简化后得到其动力学模型：

$$H(q) \ddot q + C(q, \dot q) \dot q + G(q) + F(\dot q) + \tau _d = \tau$$

其中：








F




(







q








˙









)










$F(\dot q)$
为静态和动态摩擦矩阵,











τ








d

















$\tau _d$
为建模误差和外界干扰等引起的不确定项

$$\begin{aligned} h_{11} &= I_1 + a_1 cos^2(q_2) + a_2^2cos(q_2+q_3) + 1a_3cos(q_2)cos(q_2+q_3) \\ h_{22} &= I_2 + a_1 + a_2 + 2a_3cos(q_3) \\ h_{23} &= h_{32} = a_2 + a_3 cos (q_3) \\ h_{33} &= I_3 + a_2 \\ h_{12} &= h_{13} =h_{21} =h_{31} = 0 \\ \end{aligned}$$

$$\begin{aligned} c_{11} &= -\frac{1}{2}a_1\dot q_2 sin(2q_2) -\frac{1}{2}a_2(\dot q_2 + \dot q_3)sin(2q_2 + 2q_3) - a_3 \dot q_2 sin(2q_2 + q_3) - a_3 \dot q_3 cos(2q_2)sin(q_2+q_3) \\ c_{12} &= -\frac{1}{2}a_1\dot q_1 sin(2q_2) -\frac{1}{2}a_2\dot q_1 sin(2q_2 + q_3) - a_3 \dot q_1 sin(2q_2+q_3) \\ c_{13} &= -\frac{1}{2}a_1\dot q_1 sin(2q_2 + q_3) - a_3 \dot q_1 cos(2q_2)sin(q_2+q_3) \\ c_{22} &= -a_3 \dot {q}_3 sin(q_3) \\ c_{23} &= -a_3(\dot {q}_2 + \dot {q}_3) sin (q_3)\\ c_{32} &= -a_3 \dot {q}_2 sin ( q_3)\\ c_{21} &= -c_{12} \\ c_{31} &= -c_{13} \\ c_{33} &= 0 \\ \end{aligned}$$

$$\begin{aligned} g_{1} &= 0 \\ g_{2} &= b_1 cos(q_2) + b_2 cos(q_2 + q_3) \\ g_{3} &= b_2 cos(q_2 + q_3 ) \\ \end{aligned}$$

$$\begin{aligned} f_{1} &= \mu _1 sgn( \dot q_1 ) \\ f_{2} &= \mu _2 sgn( \dot q_2 ) \\ f_{3} &= \mu _3 sgn( \dot q_3 ) \\ \end{aligned}$$

其中：












m






i















$m_i$
表示连杆的质量，











l






i















$l_i$
表示连杆的长度，











r






i















$r_i$
表示连杆质心的长度，











I








i















$I_i$
表示连杆关于其转动轴的转动惯量。








g












$g$
表示重力加速度矢量，












q








i
















$q_i$
表示连杆的转动角度（转动关节的关节变量）。

$$\begin{aligned} a_1&=m_2r_2^2 + m_3l_2^2 & a_2&=m_3r_3^2 & a_3= m_3r_3l_2 \\ b_1&=(m_2r_2 + m_3rl_2)g & b_2&=m_3r_3g & \end{aligned}$$

μ






i















$\mu_i$
为相关库伦摩擦系数，








s


g




n


(


)










$sgn()$
为符号函数

摘自：

胡盛斌，非线性多关节机器人系统滑膜控制，国防工业出版社，2015.03