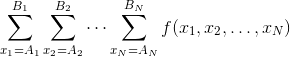博客

题目描述：

E – キャンディーとN人の子供 / Children and Candies

Time Limit: 4 sec / Memory Limit: 256 MB

Score : 800800 points

Problem Statement

12:17 (UTC): The sample input 1 and 2 were swapped. The error is now fixed.

We are very sorry for your inconvenience.

There are NN children in AtCoder Kindergarten, conveniently numbered 11 through NN. Mr.

Evi will distribute CC indistinguishable candies to the children.

If child ii is given aa candies, the child’s

happiness

will become xaixia, where xixi is the child’s

excitement level

. The

activity level

of the kindergarten is the

product

of the happiness of all

the NN children.

For each possible way to distribute CC candies to the children by giving zero or more candies

to each child, calculate the activity level of the kindergarten. Then, calculate the sum over all

possible way to distribute CC candies. This sum can be seen as a function of the children’s

excitement levels x1,..,xNx1,..,xN, thus we call it f(x1,..,xN)f(x1,..,xN).

You are given integers Ai,Bi(1≦i≦N)Ai,Bi(1≦i≦N).

Find

modulo 109+7109+7.

Constraints

• 1≦N≦4001≦N≦400
• 1≦C≦4001≦C≦400
• 1≦Ai≦Bi≦400(1≦i≦N)1≦Ai≦Bi≦400(1≦i≦N)

Partial Score

• 400400 points will be awarded for passing the test set
• satisfying Ai=Bi(1≦i≦N)Ai=Bi(1≦i≦N).

Input

The input is given from Standard Input in the following format:

NN CC
A1A1 A2A2 ... ANAN
B1B1 B2B2 ... BNBN

Output

Print the value of

modulo 109+7109+7.

Sample Input 1 Copy

Copy

2 3
1 1
1 1

Sample Output 1 Copy

Copy

4

This case is included in the test set for the partial score,

since Ai=BiAi=Bi. We only have to consider the sum of the activity level

of the kindergarten where the excitement level of both child 11 and child 22 are 11 (f(1,1)f(1,1)).

• If child 11 is given 00 candy, and child 22 is given 33 candies, the activity level of the kindergarten is 10∗13=110∗13=1.
• If child 11 is given 11 candy, and child 22 is given 22 candies, the activity level of the kindergarten is 11∗12=111∗12=1.
• If child 11 is given 22 candies, and child 22 is given 11 candy, the activity level of the kindergarten is 12∗11=112∗11=1.
• If child 11 is given 33 candies, and child 22 is given 00 candy, the activity level of the kindergarten is 13∗10=113∗10=1.

Thus, f(1,1)=1+1+1+1=4f(1,1)=1+1+1+1=4, and the sum over all ff is also 44.

Sample Input 2 Copy

Copy

1 2
1
3

Sample Output 2 Copy

Copy

14

Since there is only one child, child 11’s happiness itself will be the activity

level of the kindergarten. Since the only possible way to distribute 22 candies

is to give both candies to child 11, the activity level in this case will become

the value of ff.

• When the excitement level of child 11 is 11, f(1)=12=1f(1)=12=1.
• When the excitement level of child 11 is 22, f(2)=22=4f(2)=22=4.
• When the excitement level of child 11 is 33, f(3)=32=9f(3)=32=9.

Thus, the answer is 1+4+9=141+4+9=14.

Sample Input 3 Copy

Copy

2 3
1 1
2 2

Sample Output 3 Copy

Copy

66

Since it can be seen that f(1,1)=4,f(1,2)=15,f(2,1)=15,f(2,2)=32f(1,1)=4,

f(1,2)=15,f(2,1)=15,f(2,2)=32, the answer is 4+15+15+32=664+15+15+32=66.

Sample Input 4 Copy

Copy

4 8
3 1 4 1
3 1 4 1

Sample Output 4 Copy

Copy

421749

This case is included in the test set for the partial score.

Sample Input 5 Copy

Copy

3 100
7 6 5
9 9 9

Sample Output 5 Copy

Copy

139123417

思路：DP是弱项，想不到。。。都没看出是dp来。

dp[k][n]表示把n个糖果分给k个孩子所得到的x[i]^a[i]的乘积的加和，

就是题目要求的那玩意，感觉还挺绕呢。dp[k-1][n-m]表示把n-m个糖

果分给k-1个孩子得到的结果。也就是第k个孩子给了他m个糖果。先考

虑A[i]==B[i]的情况，这时候dp[k][n] += dp[k-1][n-m] * (A[i]^m)。当A[i] !=

B[i]的时候，则dp[k][n] += dp[k-1][n-m] * (A[i]^m + (A[i]+1)^m + … + B[i]^m)。

代码实现：

#include<bits/stdc++.h>
#define LL long long
#define INF 0x3f3f3f3f
#define io ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
const int MAXN = 405;
const LL mod = 1e9+7;
LL sum[MAXN];
LL A[MAXN],B[MAXN];
LL dp[MAXN][MAXN];
LL N,C;

LL calc(int a, int b)
{
    memset(sum,0,sizeof(sum));
    for(int i = a; i <= b; ++i)
    {
        LL t = 1;
        for(int j = 0; j <= C; ++j)
        {
            sum[j] = sum[j]+t;
            sum[j] %= mod;
            t = t*i%mod;
        }
    }
}

int main()
{
    io;
    cin >> N >> C;
    for(int i = 1; i <= N; ++i)
        cin >> A[i];
    for(int i = 1; i <= N; ++i)
        cin >> B[i];
    dp[0][0] = 1;
    for(int i = 1; i <= N; ++i)
    {
        calc(A[i],B[i]);//计算A[i]^m + (A[i]+1)^m + ... + B[i]^m
        for(int j = 0; j <= C; ++j)
            for(int k = 0; k <= j; ++k)
                dp[i][j] = (dp[i][j] + dp[i-1][j-k]*sum[k])%mod;
    }
    cout << dp[N][C] << endl;
    return 0;
}

The end;