一、对信号做降采样处理时,需要先滤波,后抽取(降采样)的原因解释:
一句话就能概括,如果抽取时不先做滤波,就会导致信号混叠,这里的滤波器是抗混叠滤波器。
1、如果不滤波,为什么混叠?
因为抽取后的
信号频谱
将以新的采样率fs为周期做频谱的延拓。
2、为什么降采样,信号频谱会延拓?
这貌似才是问题的根结,原因其实也很好解释。
时域离散化会导致频域的周期化;频域离散化会导致时域的周期化
首先,假设你要处理的信号,它长这样:
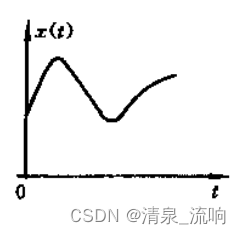
假设它在频域上,长这样:

你想处理这段信号,当然先需要通过AD采样,于是AD转换为数字信号,它从时域上看就变成了这样了:

根据“
时域是离散的意味着频域是周期的”
,这里的周期指的就是
采样频率
,就是上面那个图里面T1的倒数。现在信号在频域上可就不是原来那个样子了,而是变成这个样子:

对AD采完的
离散信号
,我们进行抽取处理,完全可以理解成对一段已经离散的信号,再进行一次“离散处理”:

也就是说,原本周期性的
频域信号
,将继续“周期”一把,于是又发生了变化:
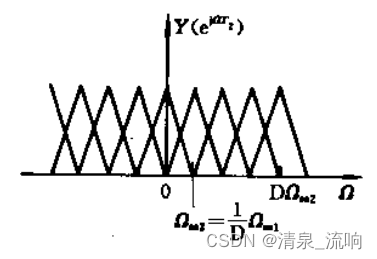
这是什么鬼?这就是所谓的混叠啊!所以赶紧的,在抽取前赶紧滤波,滤的只剩下一个“三角形”当然就不会混成这个鬼样子了。
当然也有一些聪明的小伙伴也会问,如果这个三角形的底足够窄(带宽足够小),抽的没那么狠,是不是就不会叠成这么难看了。理论上说,的确存在这种不滤波也不会混叠的情况。
但是现实中,频域上除了三角形,也会在没有三角形的地方会有一些乱七八糟的谐波啊、噪声啊什么的,所以机智的信号处理工程师们就会非常谨慎的不管什么咋地,先滤波再说!

滤波了之后,三角形被削成了竹笋,这时候再抽一把,就没那么凌乱:
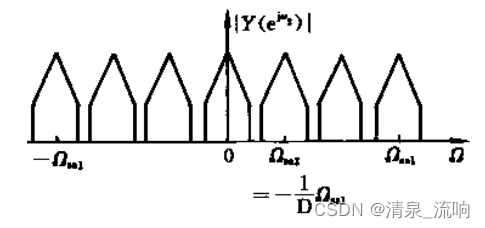
二、对信号做升采样处理时,需要先对信号进行插值(升采样),然后进行滤波操作的原因解释:
这里的滤波器称为抗镜像滤波器,不同于
抗混叠滤波器
的是,抗镜像滤波器则是必须要进行的操作,即插值完必须进行抗镜像滤波操作。这是因为直接进行插值后,采样率变大,原始的频谱的镜像会在其他地方(出现在K×fs处)。整个增采样过程如下:
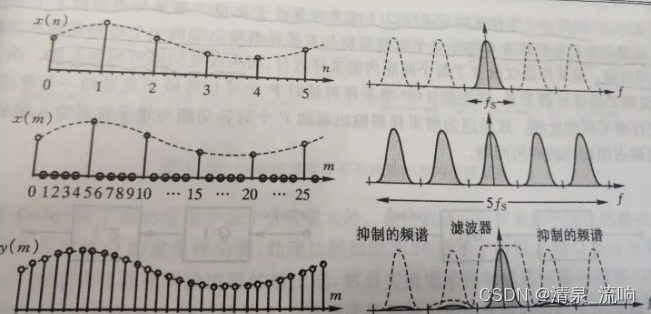
实际上,插值操作就是在两个信号点之间插入若干个0值,这样的过程就导致了频谱的
周期延拓
,为了让插值之后的波形依然平滑,此时就需要在插值之后进行平滑滤波,因此实际上抗镜像滤波也可称之为
平滑滤波器
(个人观点)。理论上的周期延拓频谱可以有具体公式去推导
,而直观上解释为啥会出现对应的插值之后就会出现高频部分的信号,可以观察x(m),从原来的两点信号中插入若干0值,这样从实际信号间从有值到0值或者从0值到有值,信号发生突变,而信号的突变就意味着信号包含丰富的高频信息(如图像的边缘、孤立点,还有矩形波)。这就出现了高频频谱,
而具体高频频谱以何种方式展现,出现在具体的那些频率则需要公式进行推导了。
三、为什么需要进行降采样和升采样的过程
直接原因当然是采用了高采样率的ADC和DAC,那为什么要用高采样ADC和DAC,答案是降低模拟滤波器(模拟抗混叠滤波器和抗镜像滤波器)的成本。评价滤波器的好坏有很多指标,对于模拟滤波器来说,很容易知道过渡带越窄,滤波器越陡,阻带衰减越大,滤波器阶数则越高,而越高阶数则意味着
模拟滤波器
越昂贵,甚至到几乎不可能实现。因此模拟滤波器的过渡带就需要设计宽一些,越宽则意味阶数越低,越容易实现,越便宜。
而宽过渡带则意味着需要更高采样率的ADC,因此ADC采样率越高,越可以降低模拟前端的设计要求。
参考文献: