欢迎访问我的博客
首页
。
PnP(Perspective-n-Point)是求解 3D 到 2D 点对运动的方法。即,知道了 n 个 3D 空间点及其投影位置,求相机的位姿变换。如下图,已知一些点在左边相机坐标系中的三维坐标,和在右边相机坐标系中的像素坐标,求这两个相机坐标系间的位姿变换,就是 PnP 问题。

图 3 PnP 问题
下面介绍四种求解 PnP 问题的方法。DLT、P3P 和 EPnP 利用若干对匹配点即可求得位姿变换,非线性优化可以利用更多观测值构造最小二乘问题。 所以,可以用前三者求得一个初始值,再用非线性优化在此初始值的基础上迭代调整。由于非线性优化通常不需要迭代很多次,所以实际使用时,可以直接使用非线性优化,在旋转矩阵为单位矩阵、平移向量为零向量的基础上直接迭代调整。
EPnP 的具体原理在
这里
。
1. DLT
DLT(Direct Linear Transform)即直接线性变换法,用 12 个参数表示增广矩阵 [R|t],因此需要至少 6 对匹配点就可以求得该增广矩阵。然后使用 QR 分解求得位姿。
2. P3P
P3P 使用 3 对匹配点求得四个解,再使用 1 对验证点得到一个合理的解。
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
double distance(const Point2f& p1, const Point2f& p2) {
return sqrt(pow(p1.x - p2.x, 2) + pow(p1.y - p2.y, 2));
}
int main() {
// 1.相机内参与畸变参数。
Mat intrinsics = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
Mat distortion = (Mat_<double>(4, 1) << 0, 0, 0, 0);
// 2.三维点。
vector<Point3f> pts_3d;
pts_3d.push_back(Point3f(-4, 2, 1));
pts_3d.push_back(Point3f(1, 2, 3));
pts_3d.push_back(Point3f(1, 3, 2));
// 3.二维点。
vector<Point2f> pts_2d;
pts_2d.push_back(cam2pix(Point3f(2, 3, 1), intrinsics));
pts_2d.push_back(cam2pix(Point3f(2, -2, 3), intrinsics));
pts_2d.push_back(cam2pix(Point3f(3, -2, 2), intrinsics));
// 4.P3P 求解。
vector<Mat> rotation_vec, translation_vec;
solveP3P(pts_3d, pts_2d, intrinsics, distortion, rotation_vec, translation_vec, SOLVEPNP_P3P);
// 5.准备一对测试点。
Mat observed_mat = (Mat_<double>(3, 1) << 2, 1, 1); // 观测值。
Point3f true_3d(1, -3, 1);
Point2f true_2d = cam2pix(true_3d, intrinsics); // 真实值。
// 6.测试。
Mat rotation_mat = Mat::zeros(3, 3, CV_64FC1);
for(int i = 0; i < rotation_vec.size(); i++) {
Rodrigues(rotation_vec[i], rotation_mat); // 旋转向量转旋转矩阵。
Mat measured_mat = rotation_mat * observed_mat + translation_vec[i];
Point3f measured_3d = Point3f(measured_mat.at<double>(0, 0),
measured_mat.at<double>(0, 1),
measured_mat.at<double>(0, 2));
Point2f measured_2d = cam2pix(measured_3d, intrinsics); // 测量值。
cout << distance(true_2d, measured_2d) << endl;
}
}
传入 solveP3P 的点对只能是 3 对或 4 对,否则会报错。无论传入的是 3 对点还是 4 对点,函数 solveP3P 都可能得出多解,需要我们自己选择正确的解。
由于我们研究的是 3D-2D 问题,所以使用函数 cam2pix 把一组 3D 点变换成了 2D 点。相机参数可以是任意的,只要在函数 cam2pix 和函数函数 solveP3P 中保持一致。
3. G2O 求解 PnP
使用非线性优化求解 PnP 问题常被称为 BA,因此 G2O 把为 PnP 问题定义的边和顶点存放在 g2o/types/sba。G2O 定义了多个求解 PnP 问题的边,下面介绍常用的 5 个边。
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV
: public BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{...};
class EdgeSE3ProjectXYZ
: public BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap> {...};
class EdgeSE3ProjectXYZOnlyPose
: public BaseUnaryEdge<2, Vector2D, VertexSE3Expmap> {...};
class EdgeStereoSE3ProjectXYZ
: public BaseBinaryEdge<3, Vector3D, VertexSBAPointXYZ, VertexSE3Expmap> {...};
class EdgeStereoSE3ProjectXYZOnlyPose
: public BaseUnaryEdge<3, Vector3D, VertexSE3Expmap> {...};
第一个边与第二个边都用于单目。它们的区别主要在于设置相机内参的方法不同:第一个边的用法在下面 3.1 节,它不包含相机内参,需要使用 optimizer.addParameter(camera) 设置相机内参;第二个边的用法参考 3.2 节,可以直接为其 fx, fy, cx, cy, bf 成员赋值。
第二个边和第三个边的区别在于是否优化三维点,所以在第二个边中固定三维点就能实现和第三个边一样的作用。第四、第五个边可以用于双目摄像头获取的二维图像,具体用法见 3.2 节。
第二个边与第四个边经常一起使用,第三个边与第五个边经常一起使用。这是因为在双目相机中,有的物方点只在其中一个相机中成像,有的物方点在两个相机中都成像。
3.1 单目
下面是使用 EdgeProjectXYZ2UV 求解 PnP 的例子。该程序只能使用 G2O 20170730 及以前版本,因为 G2O 20200410 及以后的版本定义优化器需要使用智能指针,G2O 20201223 及以后的版本用 VertexPointXYZ 替代了 VertexSBAPointXYZ。
#include <iostream>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
using namespace std;
Eigen::Vector2d cam2pix(const Eigen::Vector3d &p, const Eigen::Matrix3d &K) {
return Eigen::Vector2d((p(0) * K(0, 0)) / p(2) + K(0, 2),
(p(1) * K(1, 1)) / p(2) + K(1, 2));
}
void bundleAdjustment(const vector<Eigen::Vector3d> points_3d,
const vector<Eigen::Vector2d> points_2d,
const Eigen::Matrix3d &K,
const Eigen::Matrix3d &R, const Eigen::Vector3d &t) {
// 1.定义优化器。
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> Block;
Block::LinearSolverType *linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>();
Block *solver_ptr = new Block(linearSolver);
g2o::OptimizationAlgorithmLevenberg *solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);
// 2.位姿顶点(随意设置的初始值)。
int vertex_idx = 0;
g2o::VertexSE3Expmap *pose = new g2o::VertexSE3Expmap();
pose->setId(vertex_idx++);
pose->setEstimate(g2o::SE3Quat(R, t));
optimizer.addVertex(pose);
// 3.路标顶点。
for (const Eigen::Vector3d p : points_3d) {
g2o::VertexSBAPointXYZ *point = new g2o::VertexSBAPointXYZ();
point->setId(vertex_idx++);
point->setEstimate(p);
point->setMarginalized(true);
point->setFixed(true);
optimizer.addVertex(point);
}
// 4.添加参数(相机内参)。
int params_idx = 0;
g2o::CameraParameters *camera =
new g2o::CameraParameters(K(0, 0), Eigen::Vector2d(K(0, 2), K(1, 2)), 0);
camera->setId(params_idx);
optimizer.addParameter(camera);
// 5.边。
int edge_idx = 0;
for (const Eigen::Vector2d p : points_2d) {
g2o::EdgeProjectXYZ2UV *edge = new g2o::EdgeProjectXYZ2UV();
edge->setId(edge_idx);
edge->setVertex(0, dynamic_cast<g2o::VertexSBAPointXYZ *>(optimizer.vertex(edge_idx + 1)));
edge->setVertex(1, pose);
edge->setMeasurement(p);
edge->setParameterId(0, params_idx);
edge->setInformation(Eigen::Matrix2d::Identity());
optimizer.addEdge(edge);
edge_idx++;
}
// 6.开始迭代。
optimizer.setVerbose(true);
optimizer.initializeOptimization();
optimizer.optimize(50);
// 7.优化后的位姿。
cout << Eigen::Isometry3d(pose->estimate()).matrix() << endl;
}
int main(int argc, char **argv) {
Eigen::Matrix3d K;
K << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1;
vector<Eigen::Vector3d> pts_3d;
vector<Eigen::Vector2d> pts_2d;
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, 3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, -2, 3), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(3, -2, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(1, -3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(4, 0, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(0, -8, 3), K));
pts_3d.push_back(Eigen::Vector3d(-4, 2, 1));
pts_3d.push_back(Eigen::Vector3d(1, 2, 3));
pts_3d.push_back(Eigen::Vector3d(1, 3, 2));
pts_3d.push_back(Eigen::Vector3d(2, 1, 1));
pts_3d.push_back(Eigen::Vector3d(-1, 4, 2));
pts_3d.push_back(Eigen::Vector3d(7, 0, 3));
Eigen::Matrix3d R;
R << 1, 0, 0, 0, 1, 0, 0, 0, 1;
Eigen::Vector3d t(0, 0, 0);
bundleAdjustment(pts_3d, pts_2d, K, R, t);
}
在函数 bundleAdjustment 中,我们先定义了优化器,然后向其中添加顶点、参数、边:
- 添加顶点:第 25 行开始添加一个位姿顶点,编号为 0。第 32 行开始添加 6 个路标顶点,编号从 1 开始。
- 添加参数:第 42 行开始添加一个参数,编号为 0。
- 添加边:第 49 行开始添加 6 个边,编号从 0 开始。
每个边对应一个路标顶点,由于路标顶点编号从 1 开始,边编号从 0 开始,所以在第 54 行使用的是 edge_idx + 1。
第 54 行和第 55 行让一个二元边连接两个顶点:0 号顶点是路标 VertexSBAPointXYZ,1 号顶点是位姿 VertexSE3Expmap。顺序不能颠倒,因为边 EdgeProjectXYZ2UV 的模板参数决定了这个顺序:
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV
: public BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>{...};
第 57 行把编号为 params_idx 的参数存储在索引为 0 的参数容器中。0 号顶点会根据参数的编号从优化器中取出该参数:
// OptimizableGraph 是 EdgeProjectXYZ2UV 的基类。
bool OptimizableGraph::Edge::setParameterId(int argNum, int paramId) {
if ((int)_parameters.size() <= argNum) return false;
if (argNum < 0) return false;
*_parameters[argNum] = 0;
_parameterIds[argNum] = paramId;
return true;
}
void EdgeProjectXYZ2UV::computeError() {
// 省略。
const CameraParameters *cam = static_cast<const CameraParameters *>(parameter(0));
// 利用该参数计算投影误差。
}
下面是 CMakeLists.txt 的内容。其中,路径 D:/MinGW/libraries/g2o_20170730 是安装 G2O 的位置,包含以下文件:
bin
include
lib
FindCSparse.cmake
FindG2O.cmake
cmake_minimum_required(VERSION 3.2)
project(test)
add_compile_options(-std=c++14)
set(Eigen3_DIR D:/MinGW/libraries/share/eigen3/cmake)
find_package(Eigen3 REQUIRED)
set(G2O_ROOT D:/MinGW/libraries/g2o_20170730)
set(CMAKE_MODULE_PATH ${G2O_ROOT})
find_package(G2O REQUIRED)
find_package(CSPARSE REQUIRED)
include_directories(
${EIGEN3_INCLUDE_DIRS}
${G2O_INCLUDE_DIR}
${CSPARSE_INCLUDE_DIR}
D:/MinGW/libraries/include
)
link_directories(${G2O_ROOT}/lib)
add_executable(main main.cpp)
target_link_libraries(main
g2o_core
g2o_stuff
g2o_types_sba
g2o_types_slam3d
)
# cmake -G "MinGW Makefiles" ..
程序运行结果如下面的左图。
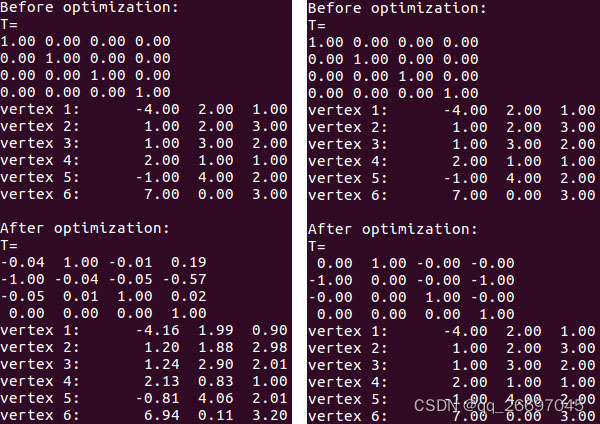
分析:可以看到计算的结果有一定的误差,尤其是平移向量 (0.19,-0.57,0.02) 与实际值 (0,-1,0) 相差较大。这是因为我们在使用 G2O 优化时同时调整了位姿与 3D 点。vertex 1 到 vertex 6 都被调整了,所以不能得到实际的位姿。但这样做在工程中却是有意义的。因为 3D 点的坐标准确度不那么可信,所以有必要把它们和位姿一块调整。如果能确定这些 3D 点的坐标是准确的,就可以得到准确的位姿,比如去掉对 point->setFixed(true) 的注释,就可以得到右图的结果。
3.2 双目
双目摄像头有视差,根据视差公式可以得到深度信息,所以使用 G2O 定义的边 EdgeStereoSE3ProjectXYZ 可以利用更多约束求解 PnP 问题。
#include <iostream>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
using namespace std;
Eigen::Vector2d cam2pix(const Eigen::Vector3d &p, const Eigen::Matrix3d &K) {
return Eigen::Vector2d((p(0) * K(0, 0)) / p(2) + K(0, 2),
(p(1) * K(1, 1)) / p(2) + K(1, 2));
}
void bundleAdjustment(const vector<Eigen::Vector3d> &points_3d,
const vector<Eigen::Vector2d> &points_2d,
const vector<int> &zs, const Eigen::Matrix3d &K,
const Eigen::Matrix3d &R, const Eigen::Vector3d &t) {
// 1.定义优化器。
typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> Block;
Block::LinearSolverType *linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>();
Block *solver_ptr = new Block(linearSolver);
g2o::OptimizationAlgorithmLevenberg *solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);
// 2.位姿顶点(随意设置的初始值)。
int vertex_idx = 0;
g2o::VertexSE3Expmap *pose = new g2o::VertexSE3Expmap();
pose->setId(vertex_idx++);
pose->setEstimate(g2o::SE3Quat(R, t));
optimizer.addVertex(pose);
// 3.路标顶点。
for (const Eigen::Vector3d p : points_3d) {
g2o::VertexSBAPointXYZ *point = new g2o::VertexSBAPointXYZ();
point->setId(vertex_idx++);
point->setEstimate(p);
point->setMarginalized(true);
point->setFixed(true);
optimizer.addVertex(point);
}
// 4.边。
int edge_idx = 0;
double bfx = K(0, 0); // baseline * fx。
double parallax;
for (const Eigen::Vector2d p : points_2d) {
g2o::EdgeStereoSE3ProjectXYZ *edge = new g2o::EdgeStereoSE3ProjectXYZ();
edge->fx = K(0, 0);
edge->fy = K(1, 1);
edge->cx = K(0, 2);
edge->cy = K(1, 2);
edge->bf = bfx;
edge->setId(edge_idx);
edge->setVertex(0, dynamic_cast<g2o::VertexSBAPointXYZ *>(optimizer.vertex(edge_idx + 1)));
edge->setVertex(1, pose);
parallax = bfx / zs[edge_idx];
edge->setMeasurement(Eigen::Vector3d(p(0), p(1), p(0) - parallax));
edge->setInformation(Eigen::Matrix3d::Identity());
optimizer.addEdge(edge);
edge_idx++;
}
// 5.开始迭代。
optimizer.setVerbose(true);
optimizer.initializeOptimization();
optimizer.optimize(50);
// 6.优化后的位姿。
cout << Eigen::Isometry3d(pose->estimate()).matrix() << endl;
}
int main(int argc, char **argv) {
Eigen::Matrix3d K;
K << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1;
vector<Eigen::Vector3d> pts_3d;
vector<Eigen::Vector2d> pts_2d;
vector<int> zs = {1, 3, 2, 1, 2, 3};
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, 3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, -2, 3), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(3, -2, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(1, -3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(4, 0, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(0, -8, 3), K));
pts_3d.push_back(Eigen::Vector3d(-4, 2, 1));
pts_3d.push_back(Eigen::Vector3d(1, 2, 3));
pts_3d.push_back(Eigen::Vector3d(1, 3, 2));
pts_3d.push_back(Eigen::Vector3d(2, 1, 1));
pts_3d.push_back(Eigen::Vector3d(-1, 4, 2));
pts_3d.push_back(Eigen::Vector3d(7, 0, 3));
Eigen::Matrix3d R;
R << 1, 0, 0, 0, 1, 0, 0, 0, 1;
Eigen::Vector3d t(0, 0, 0);
bundleAdjustment(pts_3d, pts_2d, zs, K, R, t);
}
如果有双目相机,视差是可以直接获取的。由于没有双目相机,我们在第 44 行假设基线是 1 米,在第 56 行利用像素点的深度信息生成视差信息。第 77 行是为每个像素点准备的深度信息,用在第 56 行生成视差。
从上面的程序可以看到,双目 PnP 边和单目 PnP 边用法几乎完全一样,只是测量值除了像素坐标
p
p
p
外,多了一个维度表示
p
x
p_x
p
x
与视差的差值。
4. 自定义顶点与边优化内参
下面我们将自定义顶点与边,在求解 PnP 的问题的过程中,把相机内参也当作待优化项。我们不考虑桶形畸变和枕形畸变,且只针对单目相机。如果考虑畸变,只需再加两个畸变参数,实现起来很容易。
4.1 二元边
《视觉 SLAM 十四讲 第 2 版》第 9 章的
示例程序
演示了怎么优化畸变参数,本小节就是参考该实例程序而来。
#include <iostream>
#include <sophus/se3.hpp>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_binary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/robust_kernel_impl.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
using namespace std;
struct SE3Vector4 {
SE3Vector4() {
R = Sophus::SO3d::exp(Eigen::Vector3d(0, 0, 0));
t = Eigen::Vector3d(0, 0, 0);
K = Eigen::Vector4d(0, 0, 0, 0);
}
explicit SE3Vector4(const Eigen::Matrix3d &_R, const Eigen::Vector3d &_t, const Eigen::Matrix3d &_K) {
R = Sophus::SO3d(_R);
t = _t;
K = Eigen::Vector4d(_K(0, 0), _K(1, 1), _K(0, 2), _K(1, 2));
}
Sophus::SO3d R;
Eigen::Vector3d t;
Eigen::Vector4d K;
};
class VertexSE3Vector4 : public g2o::BaseVertex<10, SE3Vector4> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
VertexSE3Vector4() {}
virtual void setToOriginImpl() override {
_estimate = SE3Vector4();
}
virtual void oplusImpl(const double *update) override {
Sophus::SO3d delta_R = Sophus::SO3d::exp(Eigen::Vector3d(update[0], update[1], update[2]));
Eigen::Vector3d delta_t = Eigen::Vector3d(update[3], update[4], update[5]);
Eigen::Vector4d delta_K = Eigen::Vector4d(update[6], update[7], update[8], update[9]);
_estimate.R = delta_R * _estimate.R;
_estimate.t = delta_t + _estimate.t;
_estimate.K = delta_K + _estimate.K;
}
Eigen::Vector2d project(const Eigen::Vector3d &point) {
Eigen::Vector3d pc = _estimate.R * point + _estimate.t;
double u = pc(0) * _estimate.K(0) / pc(2) + _estimate.K(2);
double v = pc(1) * _estimate.K(1) / pc(2) + _estimate.K(3);
return Eigen::Vector2d(u, v);
}
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
class EdgeProjectXYZKUV : public g2o::BaseBinaryEdge<2, Eigen::Vector2d, g2o::VertexSBAPointXYZ, VertexSE3Vector4> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
virtual void computeError() override {
auto v0 = (g2o::VertexSBAPointXYZ *)_vertices[0];
auto v1 = (VertexSE3Vector4 *)_vertices[1];
auto proj = v1->project(v0->estimate());
_error = proj - _measurement;
}
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
Eigen::Vector2d cam2pix(const Eigen::Vector3d &p, const Eigen::Matrix3d &K) {
return Eigen::Vector2d((p(0) * K(0, 0)) / p(2) + K(0, 2),
(p(1) * K(1, 1)) / p(2) + K(1, 2));
}
void bundleAdjustment(const vector<Eigen::Vector3d> points_3d,
const vector<Eigen::Vector2d> points_2d,
const Eigen::Matrix3d &K,
const Eigen::Matrix3d &R, const Eigen::Vector3d &t) {
// 1.定义优化器。
typedef g2o::BlockSolverX Block;
Block::LinearSolverType *linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>();
Block *solver_ptr = new Block(linearSolver);
g2o::OptimizationAlgorithmLevenberg *solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);
int vertex_idx = 0;
// 2.位姿内参顶点。
VertexSE3Vector4 *pose = new VertexSE3Vector4();
pose->setId(vertex_idx++);
pose->setEstimate(SE3Vector4(R, t, K));
pose->setFixed(false);
optimizer.addVertex(pose);
// 3.路标顶点。
for (const Eigen::Vector3d p : points_3d) {
g2o::VertexSBAPointXYZ *point = new g2o::VertexSBAPointXYZ();
point->setId(vertex_idx++);
point->setEstimate(p);
point->setMarginalized(true);
// point->setFixed(true);
optimizer.addVertex(point);
}
// 4.边。
int edge_idx = 0;
for (const Eigen::Vector2d p : points_2d) {
EdgeProjectXYZKUV *edge = new EdgeProjectXYZKUV();
edge->setId(edge_idx);
edge->setVertex(0, dynamic_cast<g2o::VertexSBAPointXYZ *>(optimizer.vertex(edge_idx + 1)));
edge->setVertex(1, pose);
edge->setMeasurement(p);
edge->setInformation(Eigen::Matrix2d::Identity());
optimizer.addEdge(edge);
edge_idx++;
}
// 5.开始迭代。
optimizer.setVerbose(true);
optimizer.initializeOptimization();
optimizer.optimize(50);
// 6.优化后的位姿和内参。
cout << pose->estimate().R.matrix() << endl;
cout << pose->estimate().t.transpose() << endl;
cout << pose->estimate().K.transpose() << endl;
}
int main(int argc, char **argv) {
Eigen::Matrix3d K;
K << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1;
vector<Eigen::Vector3d> pts_3d;
vector<Eigen::Vector2d> pts_2d;
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, 3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, -2, 3), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(3, -2, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(1, -3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(4, 0, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(0, -8, 3), K));
pts_3d.push_back(Eigen::Vector3d(-4, 2, 1));
pts_3d.push_back(Eigen::Vector3d(1, 2, 3));
pts_3d.push_back(Eigen::Vector3d(1, 3, 2));
pts_3d.push_back(Eigen::Vector3d(2, 1, 1));
pts_3d.push_back(Eigen::Vector3d(-1, 4, 2));
pts_3d.push_back(Eigen::Vector3d(7, 0, 3));
Eigen::Matrix3d R;
R << 1, 0, 0, 0, 1, 0, 0, 0, 1;
Eigen::Vector3d t(0, 0, 0);
bundleAdjustment(pts_3d, pts_2d, K, R, t);
}
结构体 SE3Vector4 用于存放自定义顶点 VertexSE3Vector4 的待优化的量:位姿和内参。类似于 g2o 为顶点 VertexSE3Expmap 定义的 SE3Quat。
自定义边 VertexSE3Vector4 时使用的模板参数是 <10, SE3Vector4>,前者指定该边的成员函数 oplusImpl 的参数数组长度,暂且称为增量维度,后者指定该边的成员变量 _estimate 的类型。
配置文件 CMakeLists.txt 内容如下。
cmake_minimum_required(VERSION 3.2)
project(test)
add_compile_options(-std=c++14)
set(Eigen3_DIR D:/MinGW/libraries/share/eigen3/cmake)
find_package(Eigen3 REQUIRED)
set(G2O_ROOT D:/MinGW/libraries/g2o_20170730)
set(CMAKE_MODULE_PATH ${G2O_ROOT})
find_package(G2O REQUIRED)
find_package(CSPARSE REQUIRED)
include_directories(
${EIGEN3_INCLUDE_DIRS}
${G2O_INCLUDE_DIR}
${CSPARSE_INCLUDE_DIR}
D:/MinGW/libraries/Sophus220401/include
D:/MinGW/libraries/fmt800/include
)
link_directories(
${G2O_ROOT}/lib
D:/MinGW/libraries/fmt800/lib
)
add_executable(main main.cpp)
target_link_libraries(main
g2o_core
g2o_stuff
g2o_types_sba
g2o_types_slam3d
g2o_types_sim3
fmt
)
# cmake -G "MinGW Makefiles" ..
4.2 三元边
下面定义三元边实现 4.1 节的功能,边连接的三个顶点是三维路标、位姿、相机内参。
#include <iostream>
#include <float.h>
#include <sophus/se3.hpp>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_binary_edge.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/robust_kernel_impl.h>
#include <g2o/solvers/eigen/linear_solver_eigen.h>
#include <g2o/types/sba/types_six_dof_expmap.h>
using namespace std;
class VertexIntrinsics : public g2o::BaseVertex<4, Eigen::Matrix3d> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
virtual void setToOriginImpl() override {
_estimate = Eigen::Matrix3d::Zero();
}
virtual void oplusImpl(const double *update) override {
_estimate(0, 0) += update[0];
_estimate(1, 1) += update[1];
_estimate(0, 2) += update[2];
_estimate(1, 2) += update[3];
}
Eigen::Vector2d project(const Eigen::Vector3d &point, const g2o::SE3Quat &T) {
Eigen::Vector3d pc = T * point;
double u = pc(0) * _estimate(0, 0) / pc(2) + _estimate(0, 2);
double v = pc(1) * _estimate(1, 1) / pc(2) + _estimate(1, 2);
return Eigen::Vector2d(u, v);
}
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
class EdgeProjectPTK : public g2o::BaseMultiEdge<2, Eigen::Vector2d> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
EdgeProjectPTK() {
this->resize(3);
}
virtual void computeError() override {
auto v0 = (g2o::VertexSBAPointXYZ *)_vertices[0];
auto v1 = (g2o::VertexSE3Expmap *)_vertices[1];
auto v2 = (VertexIntrinsics *)_vertices[2];
auto proj = v2->project(v0->estimate(), v1->estimate());
_error = proj - _measurement;
}
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};
Eigen::Vector2d cam2pix(const Eigen::Vector3d &p, const Eigen::Matrix3d &K) {
return Eigen::Vector2d((p(0) * K(0, 0)) / p(2) + K(0, 2),
(p(1) * K(1, 1)) / p(2) + K(1, 2));
}
void bundleAdjustment(const vector<Eigen::Vector3d> points_3d,
const vector<Eigen::Vector2d> points_2d,
const Eigen::Matrix3d &K,
const Eigen::Matrix3d &R, const Eigen::Vector3d &t) {
// 1.定义优化器。
typedef g2o::BlockSolverX Block;
Block::LinearSolverType *linearSolver = new g2o::LinearSolverEigen<Block::PoseMatrixType>();
Block *solver_ptr = new Block(linearSolver);
g2o::OptimizationAlgorithmLevenberg *solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);
int vertex_idx = 0;
// 2.路标顶点。
for (const Eigen::Vector3d p : points_3d) {
g2o::VertexSBAPointXYZ *point = new g2o::VertexSBAPointXYZ();
point->setId(vertex_idx++);
point->setEstimate(p);
point->setMarginalized(true);
// point->setFixed(true);
optimizer.addVertex(point);
}
// 3.位姿顶点。
g2o::VertexSE3Expmap *pose = new g2o::VertexSE3Expmap();
pose->setId(vertex_idx++);
pose->setEstimate(g2o::SE3Quat(R, t));
pose->setFixed(false);
optimizer.addVertex(pose);
// 4.内参顶点。
VertexIntrinsics *intrinsics = new VertexIntrinsics();
intrinsics->setId(vertex_idx++);
intrinsics->setEstimate(K);
// intrinsics->setFixed(true);
optimizer.addVertex(intrinsics);
// 5.边。
int edge_idx = 0;
for (const Eigen::Vector2d p : points_2d) {
EdgeProjectPTK *edge = new EdgeProjectPTK();
edge->setId(edge_idx);
edge->setVertex(0, dynamic_cast<g2o::VertexSBAPointXYZ *>(optimizer.vertex(edge_idx)));
edge->setVertex(1, pose);
edge->setVertex(2, intrinsics);
edge->setMeasurement(p);
edge->setInformation(Eigen::Matrix2d::Identity());
optimizer.addEdge(edge);
edge_idx++;
}
// 6.开始迭代。
optimizer.setVerbose(true);
optimizer.initializeOptimization();
optimizer.optimize(50);
// 7.优化后的位姿和内参。
cout << Eigen::Isometry3d(pose->estimate()).matrix() << endl;
cout << intrinsics->estimate() << endl;
}
int main(int argc, char **argv) {
Eigen::Matrix3d K;
K << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1;
vector<Eigen::Vector3d> pts_3d;
vector<Eigen::Vector2d> pts_2d;
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, 3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(2, -2, 3), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(3, -2, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(1, -3, 1), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(4, 0, 2), K));
pts_2d.push_back(cam2pix(Eigen::Vector3d(0, -8, 3), K));
pts_3d.push_back(Eigen::Vector3d(-4, 2, 1));
pts_3d.push_back(Eigen::Vector3d(1, 2, 3));
pts_3d.push_back(Eigen::Vector3d(1, 3, 2));
pts_3d.push_back(Eigen::Vector3d(2, 1, 1));
pts_3d.push_back(Eigen::Vector3d(-1, 4, 2));
pts_3d.push_back(Eigen::Vector3d(7, 0, 3));
Eigen::Matrix3d R;
R << 1, 0, 0, 0, 1, 0, 0, 0, 1;
Eigen::Vector3d t(0, 0, 0);
bundleAdjustment(pts_3d, pts_2d, K, R, t);
}
从第 35 行可以看出,定义三元边时继承了 BaseMultiEdge。和定义一元边、二元边不同的是,定义三元边时的模板参数只有增量维度和测量值类型,没有各顶点类型。在 39 行使用 resize 函数指定该边是三元边。
4.3 总结
从上面的两个程序可以看出,在位姿不固定的情况下:如果固定三维的路标顶点,无论相机内参的四个初始值与真实值相差多大,都能收敛到真实值;如果不固定路标顶点,相机内参就难以收敛到真实值,而是在初始值附近。这个原因很好解释:路标、像素坐标、位姿、内参这几项,确定的项越多,优化得到的不确定项就越准确。因此在 SLAM 中,标定相机内参很重要。
求解 PnP 问题的方法有很多,比如本文介绍的 DLT、P3P、EPnP 以及第 3、4 节使用 G2O 的非线性优化。第 3、4 节把空间点变换到相机坐标系,再投影得到像素坐标,优化的目标是使像素坐标与观测值的误差趋向 0,这就是 BA(bundle adjustment)算法。
5. 参考
-
PnP
,博客园。 -
OpenCV 中的 9 种 PnP 算法
,CSDN。 -
G2O 路标顶点的 setMarginalized 函数
,知乎专栏。