目录索引:
畅游面试中算法题集锦
一些概念:
割点
在一个
无向图
中,如果有一个顶点集合,删除这个顶点集合以及这个集合中所有顶点相关联的边以后,图的连通分量增多,就称这个点集为
割点集合
,如果某个割点集合只含有一个顶点 X(也即{X}是一个割点集合),那么X称为一个
割点
割边
在一个
无向图
中,如果有一个边集合,删除这个边集合以后,图的连通分量增多,就称这个边集为
割边集合
,如果某个割边集合只含有一条边 X(也即{X}是一个边集合),那么X称为一个
割边
,也叫做
桥
步骤
-
1.如果要找欧拉回路,可以从任意点开始,如果要找欧拉路径,需要从有着奇数度的两个及顶点中的一个开始,如果有奇数度顶点的话
-
2.选择当前点相连的边,确保删除该边,不会将欧拉图分成两个不同的联通分量
-
3.将该边加入到路径中,并将该边从欧拉图中删除,
如果当前的选择有一个桥与非桥的边时候,优先选非桥的边,不到万不得已,不选桥
-
4.持续该过程直到路径收集完成
分析
-
上面的步骤中,选桥边与非桥边的时候,
如何判断当前的边是否是桥
,这个过程很关键,大体的思路是:-
从当前节点
u
出发,计数,哪些顶点可以通过
u
可达,直接可达和间接可达均可以,记为
count1
-
移除掉
u-v
这条边 -
从当前节点
v
出发,,哪些顶点可以通过
v
可达,直接可达和间接可达均可以,记为
count2
-
恢复
u-v
这条边 -
返回
count1
与
count2
的大小,如果
count2
要比
count1
小,说明移除
u-v
这条边,从v可达的顶点数量减少,产生了额外的联通分量,此时返回
falase
,说明这条边是桥,反之返回
true
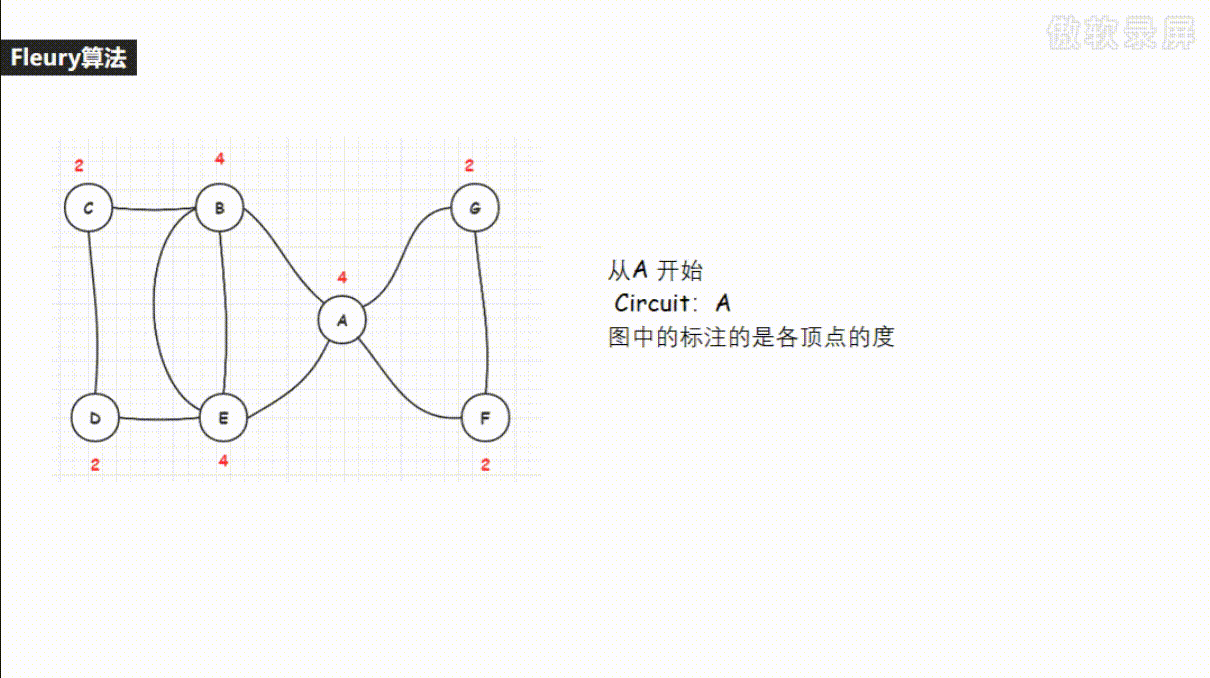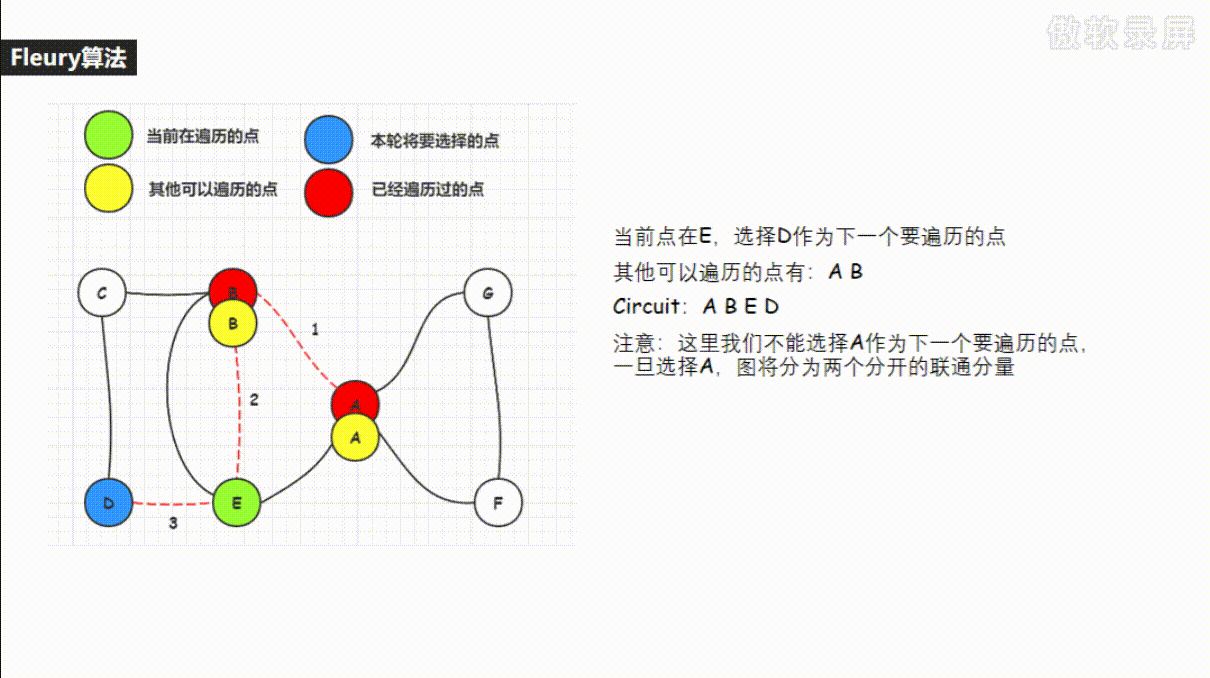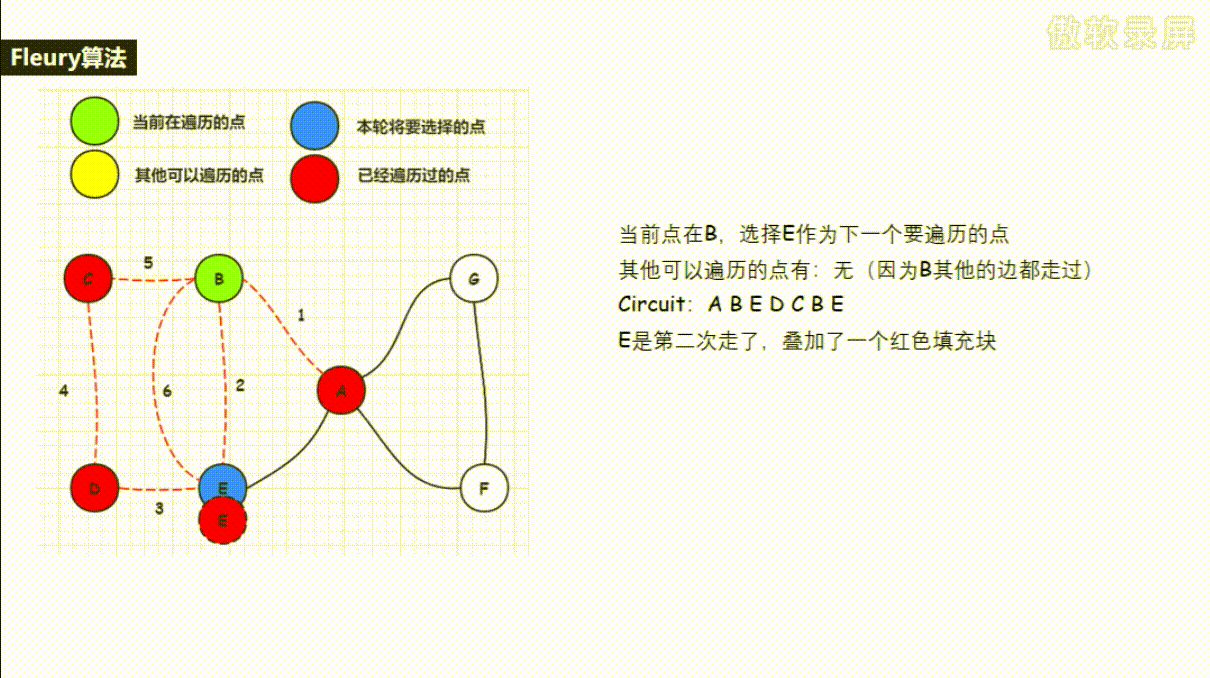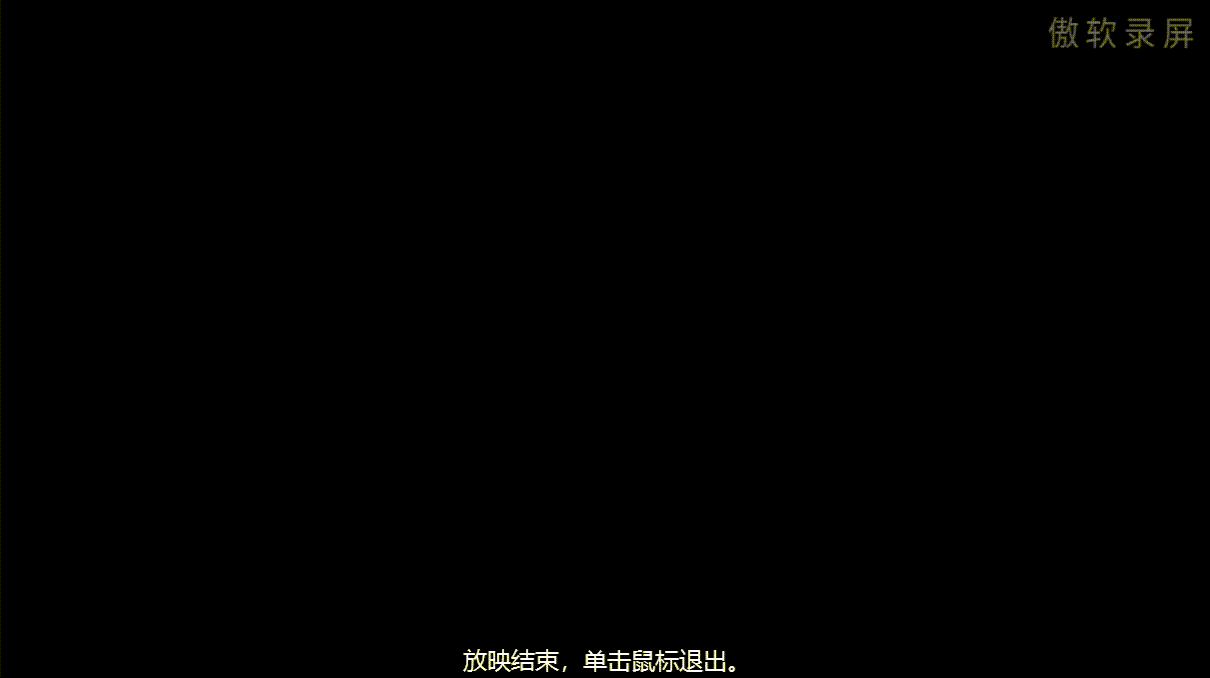
-
从当前节点
图结构 Graph
/**
* 图结构
*/
public static class Graph {
private static int vertices; //顶点的数量
private static ArrayList<Integer>[] adj; // 邻接表
Graph(int vertices) {
this.vertices = vertices;//复制
initGraph();
}
// 初始化邻接表
private static void initGraph() {
adj = new ArrayList[vertices];
for (int i = 0; i < vertices; i++) {
adj[i] = new ArrayList<>();
}
}
// 添加边u-v
private static void addEdge(Integer u, Integer v) {
adj[u].add(v);
adj[v].add(u);
}
// 移除边u-v
private static void removeEdge(Integer u, Integer v) {
adj[u].remove(v);
adj[v].remove(u);
}
}
Fleury算法核心类 FleuryProcess
public static class FleuryProcess {
/**
* 入口类
*/
public static void printEulerTour() {
//找到起点,如果没有奇数度的点,从0开始
int u = 0;
for (int i = 0; i < Graph.vertices; i++) {
if (Graph.adj[i].size() % 2 == 1) {
u = i;
break;
}
}
printEulerUtil(u);
}
/**
* 打印欧拉路径
* @param u 当前处理的顶点
*/
private static void printEulerUtil(Integer u) {
for (int i = 0; i < Graph.adj[u].size(); i++) {
Integer v = Graph.adj[u].get(i);
if (isValidNextEdge(u, v)) {
System.out.printf("%d->%d ", u, v);
Graph.removeEdge(u, v);
printEulerUtil(v);
}
}
System.out.println();
}
/**
* 判断u-v是否是桥 桥与非桥
* @param u
* @param v
* @return
*/
private static boolean isValidNextEdge(Integer u, Integer v) {
if (Graph.adj[u].size() == 1) return true;//当前只有条边,返回
boolean[] visited = new boolean[Graph.vertices];//顶点的访问数组
int count1 = dfs(u, visited);//获得count1
Graph.removeEdge(u, v);//移除边
visited = new boolean[Graph.vertices];
int count2 = dfs(u, visited);//获得count2
Graph.addEdge(u, v);//恢复边
return count1 <= count2;
}
/**
* 计算当前点v 可达的顶点数量
* @param v
* @param visited
* @return
*/
private static int dfs(Integer v, boolean[] visited) {
visited[v] = true;//标记
int count = 1;
for (int adj : Graph.adj[v]) {
if (!visited[adj]) {
count += dfs(adj, visited);
}
}
return count;
}
}
测试类 Test
public class Test{
public static void main(String[] args) {
FleuryProcess handler = new FleuryProcess();
Graph graph = new Graph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(2, 3);
handler.printEulerTour();
graph = new Graph(3);
graph.addEdge(0, 1);
graph.addEdge(1, 2);
graph.addEdge(2, 0);
handler.printEulerTour();
graph = new Graph(5);
graph.addEdge(1, 0);
graph.addEdge(0, 2);
graph.addEdge(2, 1);
graph.addEdge(0, 3);
graph.addEdge(3, 4);
graph.addEdge(3, 2);
graph.addEdge(3, 1);
graph.addEdge(2, 4);
graph = new Graph(3);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(2, 0);
handler.printEulerTour();
}
}
//打印结果:
2->0 0->1 1->2 2->3
0->1 1->2 2->0
0->2 2->0 0->1
Reference
版权声明:本文为wat1r原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。