作为研究生的入门课，数值计算的大作业算是所有研究生开学的重要编程作业。

我把最小二乘算法在MATLAB中整合成了一个M函数文件least square fitting.m，直线拟合函数lsf_linear.m，以及抛物线拟合函数lsf_parabolic.m。程序放在文章最后了，需要的同学自取。下文为作业详解

题目：根据降雨量的数据拟合流速余降雨量函数

在水资源工程学中，水库的大小与为了蓄水而拦截的河道中的水流速度密切相关。 对于某些河流来说，这种长时间的历史水流记录很难获得。然而通过容易得到过去若干年间关于降水量的气象资料。鉴于此，推导出流速与降水量之间的关系式往往特别有用。 只要获得那些年份的降水量数据，就可以利用这个关系式计算出水流速度。下表是在被水库拦截的某河道中测得的数据

数学原理：



最小二乘法多项式曲线拟合，根据给定的m个点,并不要求这条曲线精确地经过这些点，而是曲线y=f(x)的近似曲线y=φ(x)。

在实际运算过程中，给定数据点pi(xi,yi)，其中i=1,2,…,m。求近似曲线y= φ(x)。并且使得近似曲线与y=f(x)的偏差最小。近似曲线在点pi处的偏差为δi= φ(xi)-y，i=1,2,…,m。按偏差平方和最小的原则选取拟合曲线，并且采取二项式方程为拟合曲线的方法,称为最小二乘法。

本次大作业中，建立的两个一维向量RF（rainfall）,FV(flow velocity)分别代表的是表中测量数据的降水量和流速。工作目录中建立的两个功能函数，

function


f=lsf_parabolic(x)


为


抛物线最小二乘拟合

function f=lsf_parabolic(x)
% 抛物线最小二乘拟合
f(1)=1;
f(2)=x;
f(3)=x^2;
end

function


f=lsf_linear(x)


为


直线最小二乘拟合

function f=lsf_linear(x)
% 直线最小二乘拟合
f(1)=1;
f(2)=x;
end

拟合过程：



对于给定的一组数据{(x,y)}n假定拟合函数为

Φ(x)=a0Φ0(x)+a1Φ1(x)+……+anΦn(x)

其中基函数为线性无关的函数系，最小二乘拟合问题就是求系数，使得所有拟合值和实际值的平方差去极小值。因此利用给定的两个一维向量构建系数矩阵和结果矩阵，再利用这两个矩阵构建法方程。

如此最小二乘拟合问题就转化为超定线性方程组：

Ax=y

因此本实验要点就在于



构建法方程并解出相应拟合图像拟合出的拟合函数

实验过程及结果如下

1.绘制数据离散点图形

RF=[88.9 108.5 104.1 139.7 127 94 116.8 99.1];
FV=[14.6 16.7 15.3 23.2 19.5 16.1 18.1 16.6];
plot(RF,FV,'r.');
grid on；
xlabel('x');
ylabel('y');

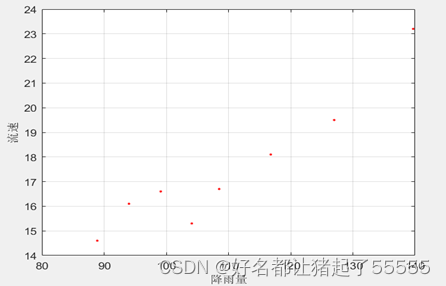
2.利用直线进行最小二乘拟合，将拟合直线添加到离散点图形上

程序在附录中，并给出具体注释

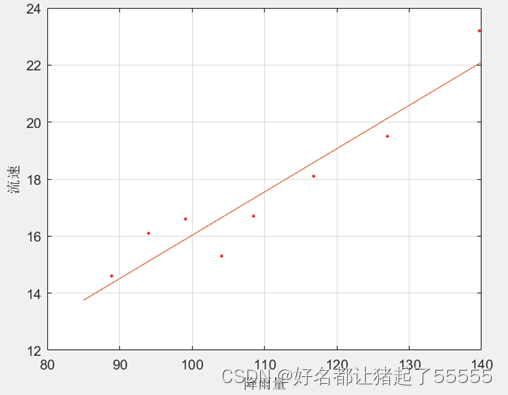
结论：

根据拟合过程，可知图像中所有离散点到拟合直线绝对距离之和比其他所有直线都小。

3.利用抛物线进行最小二乘拟合，将拟合抛物线添加到离散点图形上

程序在附录中，并给出具体注释

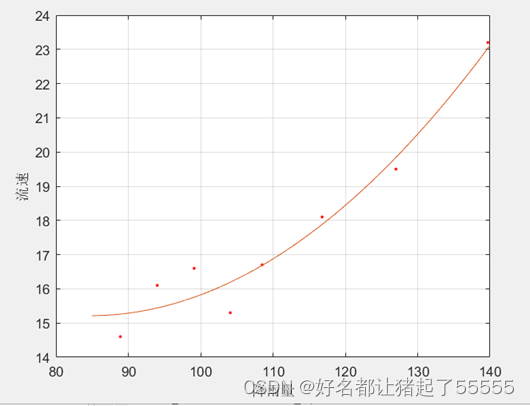
结论：

根据拟合过程，可知图像中所有离散点到拟合抛物线的绝对距离之和的比其他所有抛物线都小

4.若某年的降水量是




120cm




，利用拟合直线估计当年的水流速度

% 若某年的降水量是 120cm，利用拟合直线估计当年的水流速度,并展示
RF_4=120;
FV_4=C(1)*1+C(2)*RF_4;
disp(FV_4);

结论：

利用第二问拟合直线方程，可直接计算出当降水量为120cm时水流速度为19.0673m2/s

% least square fitting.m
% 设置两个一维向量，降水量RF和流速FV
RF=[88.9 108.5 104.1 139.7 127 94 116.8 99.1]';
FV=[14.6 16.7 15.3 23.2 19.5 16.1 18.1 16.6]';
%单独绘制离散图形
% plot(RF,FV,'r.')
% 写最小二乘拟合基函数
% 形成线性方程的系数矩阵,若采用直线进行拟合a=zeros(m,2),拟合函数为lsf_linear；用抛物线则为a=zeros(m,3)，拟合函数为lsf_parabolic
m=length(RF);
a=zeros(m,3);
for i=1:m
  a(i,:)=lsf_parabolic(RF(i));
end
 b=FV;
% 法方程,以及求解各系数放置于C中
A=a'*a;
B=a'*b;
C=A\B;
%画图拟合曲线图像以及原离散图形，直线拟合y_nh=C(1)*1+C(2)*plotx;抛物线拟合则为y_nh=C(1)*1+C(2)*plotx+C(3)*plotx.^2;
plotx=85:0.01:140;
y_nh=C(1)*1+C(2)*plotx+C(3)*plotx.^2;
plot(RF,FV,'r.',plotx,y_nh);
grid on
xlabel('降雨量');
ylabel('流速');
% 若某年的降水量是 120cm，利用拟合直线估计当年的水流速度,并展示
% RF_4=120;
% FV_4=C(1)*1+C(2)*RF_4;
% disp(FV_4);
    function f=lsf_linear(x)
   % 直线最小二乘拟合
    f(1)=1;
    f(2)=x;
    end
function f=lsf_parabolic(x)
% 抛物线最小二乘拟合
f(1)=1;
f(2)=x;
f(3)=x^2;
end