博客

⭐

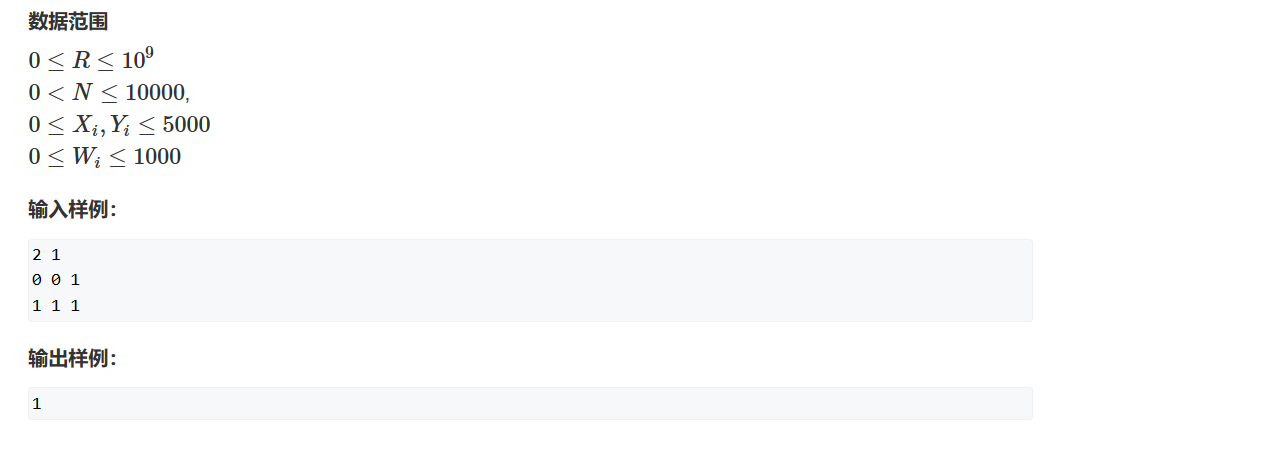
原题地址

🤠 1 MB = 1 兆 = 1024 * 1024 Byte ≈ 10^6 Byte = 250 000 个 int

🤠 128 MB ≈ 32 000 000 （三千两百万个） int

🤠 由于本题内存限制比较苛刻，所以只开一个二维数组，前边记录 前n项的值 后边记录前n项和

😤 避坑

① 价值在 交点上面，并不是在方格里边
② 读入价值的时候需要用 += ，因为每个点上的价值会重复叠加
③ 前缀和数组需要处理到 5001 ，必须大于数据范围 1 以上才可能实现堆 右下角的 点 实现覆盖
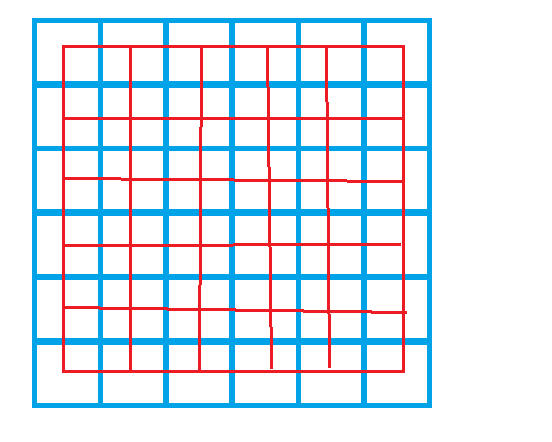
④ r * r 的正方形 只能覆盖 r * r 个点，边缘上的点并不会被炸到，如下图所示
⑤ r 最大到 5001 就已经可以覆盖全局了，再大也是这个结果

👨‍🏫 前缀和 思维转变

值存交点 -> 存格子中间
在交点存值的方格外面 再加上一层方格，这样 值 就可以放在格子中间了，也就是常见的二维前缀和思路
注意 ：边长得开大一个空间

😋 好了，又是一个背出来的前缀和模板，代码如下

import java.io.*;
 
public class Main
{
	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
	static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
	static int N = 5010;

	static int[][] s = new int[N][N];

	public static void main(String[] args) throws NumberFormatException, IOException
	{
		String[] split = in.readLine().split(" ");
		int n = Integer.parseInt(split[0]);
		int r = Integer.parseInt(split[1]);

		for (int i = 0; i < n; i++)
		{
			String[] split2 = in.readLine().split(" ");
			int x = Integer.parseInt(split2[0]);
			int y = Integer.parseInt(split2[1]);
			int w = Integer.parseInt(split2[2]);
			s[x + 1][y + 1] += w;// 细节 += （一个位置可能有多个目标）
		}

//		预处理前缀和数组
		for (int i = 1; i <= 5001; i++)
			for (int j = 1; j <= 5001; j++)
			{
				s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
			}

		int res = 0;
		r = Math.min(r, 5001);
		for (int i = r; i <= 5001; i++)
			for (int j = r; j <= 5001; j++)
			{
				res = Math.max(res, s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r]);
			}

		out.write(res + "");
		out.flush();
	}
}