说明
自己整理,欢迎交流~
2.1 数据集包含1000个样本,其中500个正例、500个反例,将其划分为包含70%样本的训练集和30%样本的测试集用于留出法评估,试估计有多少种划分方式。
答:30%用于测试集相当于要从正负样本各选500*30%=150个样本
所以一共有
C
500
150
⋅
C
500
150
C_{500}^{150}·C_{500}^{150}
C
5
0
0
1
5
0
⋅
C
5
0
0
1
5
0
2.2 数据集包含100个样本,其中正、反例各一半,假定学习算法所产生的模型试将新样本预测为训练样本数较多的类别(训练样本数相同时进行随机猜测),试给出用10折交叉验证法和留一法分别对错误率将性评估所得的结果。
答:10折交叉验证每次验证集上的正负样本理想状态下可理解为正负各一半,训练样本也是正负各一半,所以预测准确率是50%;留一法可分为2种情况理解,留下的样本是正例,则训练样本种正样本49,负样本50,预测为负样本,预测错误,同理,留下的是负样本,则预测为正样本也预测错误,故留一法预测错误率为100%。
2.3 若学习器A 的F1值笔学习器B高,试析A的BEP值是否也比B高。
答:
首先说下概念:
- BEP(Break-Even Point):是 P=R时的取值
-
F1:
F1
=
2
∗
P
∗
R
P
+
R
F1=\frac{2*P*R}{P+R}
F
1
=
P
+
R
2
∗
P
∗
R
则:
-
若P=R, 则F1=P=R=BEP,
-
若
F1
A
>
F
1
B
F1_A > F1_B
F
1
A
>
F
1
B
, 则
BE
P
A
>
B
E
P
B
BEP_A >BEP_B
B
E
P
A
>
B
E
P
B
-
若
- 若P != R,在PR曲线上,每个(P,R)点都对应一个F1值,这时可以看出F1和BEP并没有相关的关系,可以说BEP是F1的特殊情况,并不能代表全局情况。
2.4 试述真正例率(TPR),假正例率(FPR)、查准率(P)、查全率(R)之间的关系。
答:
-
TP
R
=
T
P
T
P
+
F
N
TPR=\frac{TP}{TP+FN}
T
P
R
=
T
P
+
F
N
T
P
-
FP
R
=
F
P
F
P
+
T
N
FPR=\frac{FP}{FP+TN}
F
P
R
=
F
P
+
T
N
F
P
-
P=
T
P
T
P
+
F
P
P=\frac{TP}{TP+FP}
P
=
T
P
+
F
P
T
P
-
R=
T
P
T
P
+
F
N
R=\frac{TP}{TP+FN}
R
=
T
P
+
F
N
T
P
由上面的公式可以看出,TPR=R,其他公式之间并没有关系。
2.5 试证明式(2.21)
式2.22:
A
U
C
=
1
−
l
r
a
n
k
AUC=1-l_{rank}
A
U
C
=
1
−
l
r
a
n
k
答:
A
U
C
=
1
2
∑
i
=
1
m
−
1
(
x
i
+
1
−
x
i
)
(
y
i
+
y
i
+
1
)
AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)(y_i+y_{i+1})
A
U
C
=
2
1
i
=
1
∑
m
−
1
(
x
i
+
1
−
x
i
)
(
y
i
+
y
i
+
1
)
l
r
a
n
k
=
1
m
+
m
−
∑
x
+
∈
D
+
∑
x
−
∈
D
−
(
I
I
(
f
(
x
+
)
<
f
(
x
−
)
)
+
1
2
I
I
(
f
(
x
+
)
=
f
(
x
−
)
)
)
l_{rank}=\frac{1}{m_+m_-}\sum_{x^+\in{D^+}}\sum_{x^-\in{D^-}}(II(f(x^+)<f(x^-))+\frac{1}{2}II(f(x^+)=f(x^-)))
l
r
a
n
k
=
m
+
m
−
1
x
+
∈
D
+
∑
x
−
∈
D
−
∑
(
I
I
(
f
(
x
+
)
<
f
(
x
−
)
)
+
2
1
I
I
(
f
(
x
+
)
=
f
(
x
−
)
)
)
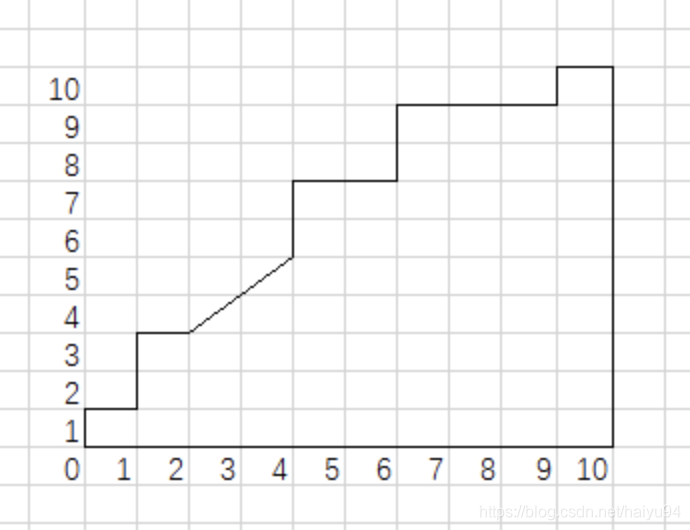
公式2.21累加了所有不在正例的反例数目,其中同样的位置标记为0.5,在正例前面标记为1,从图2.4的ROC曲线可以看出,曲线每次向右上延伸,说明遇到了反例,折线上方对应的面积,就是该反例后面有多少个正例,每个正例是一个正方形,对应的面积是1。同位置上的正例是个三角形,对应的面积是0.5。计算出总面积后,由于ROC图的坐标是归一化的,所以总面积要除以一开始放大的倍数,也就是
m
+
m
−
m^+m^−
m
+
m
−
。
注:图文参考:https://www.cnblogs.com/daigz1224/p/7163342.html
2.6 试述错误率与ROC曲线的关系
答:
ROC曲线每个点对应TPR,FPR
错误率
E
(
f
;
D
)
=
1
m
∑
i
m
I
I
(
f
(
x
i
)
!
=
y
i
)
=
F
P
+
F
N
m
+
+
m
−
=
F
P
+
m
+
−
T
P
m
+
+
m
−
=
m
−
∗
F
P
m
−
+
m
+
∗
(
1
−
T
P
m
+
)
m
+
+
m
−
=
m
−
∗
F
P
R
+
m
+
∗
(
1
−
T
P
R
)
m
+
+
m
−
E(f;D)=\frac{1}{m}\sum_i^mII(f(x_i) !=y_i)=\frac{FP+FN}{m^++m^-}=\frac{FP+m^+-TP}{m^++m^-}=\frac{m^-*\frac{FP}{m^-}+m^+*(1-\frac{TP}{m^+})}{m^++m^-}=\frac{m^- * FPR + m^+ * (1-TPR)}{m^++m^-}
E
(
f
;
D
)
=
m
1
i
∑
m
I
I
(
f
(
x
i
)
!
=
y
i
)
=
m
+
+
m
−
F
P
+
F
N
=
m
+
+
m
−
F
P
+
m
+
−
T
P
=
m
+
+
m
−
m
−
∗
m
−
F
P
+
m
+
∗
(
1
−
m
+
T
P
)
=
m
+
+
m
−
m
−
∗
F
P
R
+
m
+
∗
(
1
−
T
P
R
)
2.7 试证明任意一条ROC曲线都有一条代价曲线与之对应,反之亦然。
答:

ROC曲线上的每个点对应的是(FPR,TPR),由此可以得到FPR和FNR,从而绘制上图中的从(0,FPR)到(1,FNR)的险段,线段下面的面积为该条件下的期望总体代价,所有线段的下界围成代价曲线。
2.8 min-max规范化和z-score规范化是两种常见的规范化方法,令
x
x
x
和
x
′
x’
x
′
分别表示变量在规范化前后的取值,相应的,令
x
m
i
n
x_{min}
x
m
i
n
和
x
m
a
x
x_{ma x}
x
m
a
x
表示规范化前的最小值和最大值,
x
m
i
n
′
x_{min}’
x
m
i
n
′
和
x
m
a
x
′
x_{max}’
x
m
a
x
′
表示规范化后的最小值和最大值,
x
ˉ
\bar{x}
x
ˉ
和
σ
x
\sigma_x
σ
x
分别表示规范化前的均值和标准差,则min-max规范化、z-score规范化分别如下式所示,试分析二者的优缺点。
x
′
=
x
m
i
n
′
+
x
−
x
m
i
n
x
m
a
x
−
x
m
i
n
∗
(
x
m
a
x
′
−
x
m
i
n
′
)
x’=x’_{min} + \frac{x-x_{min}}{x_{max}-x_{min}} * (x’_{max}-x’_{min})
x
′
=
x
m
i
n
′
+
x
m
a
x
−
x
m
i
n
x
−
x
m
i
n
∗
(
x
m
a
x
′
−
x
m
i
n
′
)
x
′
=
x
−
x
ˉ
σ
x
x’=\frac{x-\bar{x}}{\sigma_x}
x
′
=
σ
x
x
−
x
ˉ
答:
- min−max规范化方法简单,保证规范化后所有元素都是正的且在(0,1)之间,每当有新的元素进来,只有在该元素大于最大值或者小于最小值时才要重新计算全部元素。但是若存在一个极大(小)的元素,会导致其他元素变的非常小(大)。
- z−score标准化对个别极端元素不敏感,保证规范化后所有元素都是正的且在(0,1)之间,且把所有元素分布在0的周围,一般情况下元素越多,0周围区间会分布大部分的元素,每当有新的元素进来,都要重新计算方差与均值。
2.9 试述
χ
2
\chi^2
χ
2
检验过程
答案见:
链接
2.10 试述Friedman检验中使用试2.34和式2.35的区别
(待更新)