有句老话说得好,学会了0-1背包就学会了算法。本篇博客就来盘点一下0-1背包的4种常见解法。
动态规划法
既然要用动态规划法解0-1背包问题,就要能满足动态规划的两个特性:
- 具有重叠子问题。
-
具有最优子结构性。
这两点应该很容易就可以看出,这里就不做过多赘述了。
直接来看关键,之前说过,动态规划的本质就是填表,而解动态规划问题的关键是找出动态转移方程,一旦找出动态转移方程,就可以用方程把整个表都填满了。
这里直接给出动态转移方程
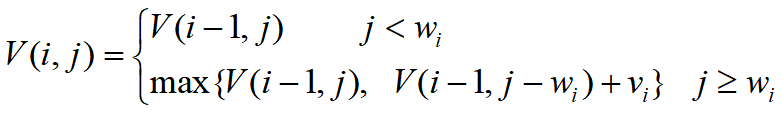
V(i, j)表示在前i(1≤i≤n)个物品中能够装入容量为j(1≤j≤C)的背包中的物品的价值最大值。
第一个式子表明:如果第i个物品的重量大于背包的容量,则物品i不能装入背包,那么装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价值是相同的。
第二个式子表明:如果第i个物品的重量小于背包的容量,则物品i能装入背包,则会有以下两种情况:
1、如果背包足够大,在不取出之前物品的情况下,还可以再放入当前物品,那就直接放。
2、如果背包不是足够大,如果要放入当前物品,就要取出其他的物品来腾空间,这时候就要考虑要不要放。我们可以做一个比较。将不装当前物品的价值V(i-1,j)和把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi进行比较;显然,取二者中价值较大者作为把前i个物品装入容量为j的背包中的最优解。
下面举例来说明:
设背包容量为5,有五个物品:

之前说过,动态规划的本质就是填表,一旦找出动态转移方程,就可以用方程把整个表都填满了。
这里我们先将空表画出来,i表示物品,j表示背包容量。
容易看出,当J=0(背包容量为0)时,背包价值永远为0,故第一列全为0.
当i=0(没有物品)时,背包价值永远为0,故第一行全为0.

接下来我们开始用动态转移方程填表。
当I=1时,我们算出V(1,1),V(1,2),V(1,3),V(1,4),V(1,5)

当I=2时,我们算出V(2,1),V(2,2),V(2,3),V(2,4),V(2,5)

以此类推,填完整张表。

表填完了,那么我们怎么知道最优解是什么呢?
首先我们找到价值最大的一个,即37,然后从他开始,和他上面的格子比较,如果不相等,就说明该元素被放入了背包。然后将背包容量减去改物品的重量,继续之前的方法。
例如:
m[4,5] != m[3,5],i4在最优解中。j=5-2
m[3,3] = m[2,3],i4不在最优解中
m[2,3]!= m[1,3], i2在最优解中。j=3-1
m[1,2] != m[0,2], i1在最优解中。j=2-2
故,放入物品1,2,4背包价值最大。
贪心法
贪心法其实并不能够解决0-1背包问题,因为在0-1背包问题中,物品是不可拆分的,如果我们假设物品可以拆分,即可以装入1/2个物品或者1/4个物品等,那么问题就可以用贪心法来解决了。
贪心法解决背包问题的思路很简单,我们用物品价值/物品重量,得到物品的单位价值,然后按单位价值排序,再往里面按顺序装就行了,如果最后一个物品装不下了,就把物品拆分,把背包的空装满就行。
public class test{
public void tanxin()
{
float rest= bag;
int j=0;
float b=0;
for(int i=2;i>=0;i--)
{
if(goods[i].weight<=rest)
{
goods[i].bn=goods[i].weight;
goods[i].an=goods[i].value;
rest=rest-goods[i].weight;
b=b+goods[i].value;
j++;
}
else if(rest>0){
float a =(float)rest/goods[i].weight;
goods[i].an=goods[i].value*a;
goods[i].bn=goods[i].weight*a;
b=b+(goods[i].value*a);
rest=0;
}
}
回溯法
首先我们将物品安装单位价值排序。
V表示物品的价值
w表示物品的重量
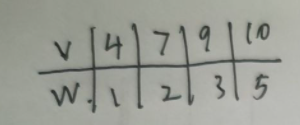
然后用上文提到的贪心法计算一个上界:22
背包初始大小为7
设置一个剪枝函数
:如果cv(当前价值)+r(剩余价值)>=22,才进入右子树,否则直接跳过右子树,不用计算。
下面开始深度优先遍历子集树:
我们定义两个变量:
cv表示当前背包中所有物品的价值总和
CJ表示当前背包中剩余的空间

我们将第1个物品放入,进入1的左子树,此时cv(当前价值)=4,cj(背包剩余容量)=6
我们将第2个物品放入,进入2的左子树,此时cv(当前价值)=11,cj(背包剩余容量)=4
我们将第3个物品放入,进入3的左子树,此时cv(当前价值)=20,cj(背包剩余容量)=1
我们将第4个物品放入,进入4的左子树,此时背包剩余容量不足不能够放入,故左子树走不通。
回溯,通过剪枝函数考察4的右节点,cv+r>22,所以进入右子树,到达叶子节点,这一条路径就是0-1背包的一个解cv=20(不一定是最优解)。
回溯,通过剪枝函数考察3的右节点,cv+r<22,减枝
回溯,通过剪枝函数考察2的右节点,cv+r>22,所以进入2的右子树,
我们将第3个物品放入,进入7的左子树,此时cv(当前价值)=13,cj(背包剩余容量)=3
我们将第4个物品放入,进入8的左子树,背包剩余容量不足,故左子树走不通。
回溯,通过剪枝函数考察8的右节点,cv+r>22,所以进入右子树,到达叶子节点,这一条路径就是0-1背包的一个解cv=13(不一定是最优解)。
回溯,通过剪枝函数考察7的右节点,cv+r<22,减枝。
回溯,通过剪枝函数考察1的右节点,cv+r>22,所以进入右子树,
我们将第2个物品放入,进入11的左子树,此时cv(当前价值)=7,cj(背包剩余容量)=5
我们将第3个物品放入,进入12的左子树,此时cv(当前价值)=16,cj(背包剩余容量)=2
我们将第4个物品放入,进入13的左子树,背包剩余容量不足,故左子树走不通。
回溯,通过剪枝函数考察13的右节点,cv+r>22,所以进入右子树,到达叶子节点,这一条路径就是0-1背包的一个解cv=16(不一定是最优解)。
回溯,通过剪枝函数考察12的右节点cv+r<22,减枝。
回溯,通过剪枝函数考察11的右节点cv+r<22,减枝。
至此,子集树的深度遍历完成,我们得到了0-1背包的三个解,取其中最大的一个cv=20,即是0-1背包的最优解。
public void backtrack(int i)
{
if (i>n-1)
{
if(cp>bestp)
{
bestp = cp;
for(int x=0;x<n;x++)
{
fin[x]=put[x];
}
}
return;
}
if (cw + goods[i].weight <= c)
{
cw += goods[i].weight;
cp += goods[i].value;
put[i] = 1;
backtrack(i + 1);
cw -= goods[i].weight;
cp -= goods[i].value;
put[i] = 0;
}
if (bound(i + 1) > bestp)
{
backtrack(i + 1);
}
}
//计算上界函数,功能为剪枝
public double bound(int i)
{ //判断当前背包的总价值cp+剩余容量可容纳的最大价值<=当前最优价值
double leftw = c - cw;
double b = cp;//最大价值
while (i <= n-1 && goods[i].weight <= leftw)
{
leftw -= goods[i].weight;
b += goods[i].value;
i++;
}
//装满背包
if (i <= n-1)
b += goods[i].value / goods[i].weight * leftw;
return b;//返回计算出的上界
}
分支限界法
分支限界法和回溯法的区别,一个是广度优先,一个是深度优先。
这里我们直接用广度优先来遍历子集树就行了。
0-1背包的子集树

首先我们将物品安装单位价值排序。

然后计算一个上界和下界:
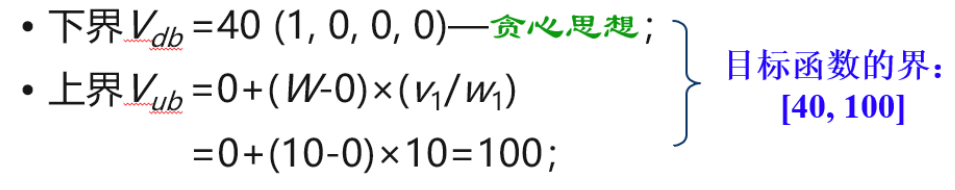
下界是指,背包里只装第一个物品,其他都不装,此时背包的价值达到最小。
上界是假设第一个物品正好把背包装满,因为第一个物品的单位价值最高,此时背包的价值达到最大。
那么实际的最优情况应该介于两者之间,越大越好。如果超出这个界限,就直接舍弃掉。
此外,我们需要设定一个界限函数ub,这个界限函数的作用是帮我们计算,在当前状况下我们背包最后可以达到的最高价值。

最后我们设置一个队列PT{}来存放活结点。
下面我们开始按广度优先的方式遍历子集树。

首先,从第一个物品开始,计算它的左孩子(放入第一个物品)和右孩子(不放第一个物品)。计算完成后,我们发现2节点的ub比3大,所以2应该排在3前面,于是此时PT{2,3}。
接下来计算2节点的左孩子(放入第2个物品)和右孩子(不放第2个物品),计算完成后,我们发现4节点超出了背包大小,5节点的ub比3节点大,所以5节点应该排在3节点前面,于是此时PT{5,3}。
接下来计算5节点的左孩子(放入第3个物品)和右孩子(不放第3个物品),计算完成后,6节点的ub比7节点大,7节点的ub比3节点大,所以6节点应该排在7节点前面,7节点应该排在3节点前面,于是此时PT{6,7,3}。
接下来计算6节点的左孩子(放入第4个物品)和右孩子(不放第4个物品),计算完成后,我们发现8节点超出了背包大小,9节点到达了叶子节点,根据分支限界的规则,算法结束。