运算方法和运算器

一、基本的二进制加法/减法器

半加器

不考虑进位

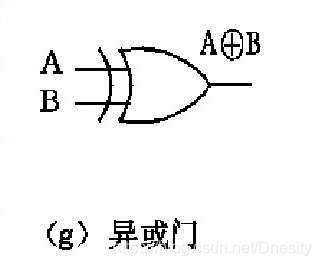
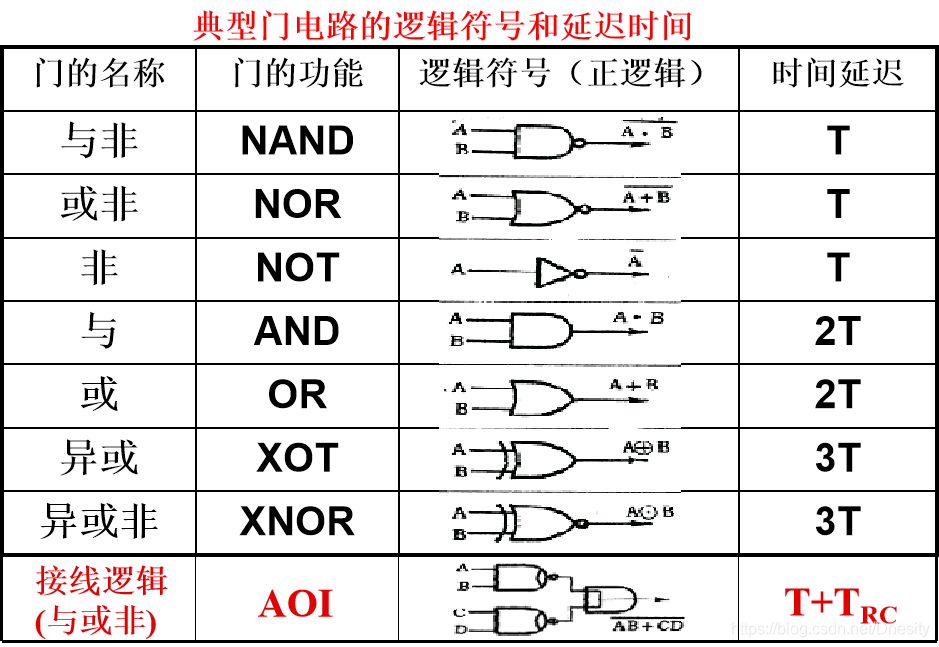
各种逻辑门的图形符号

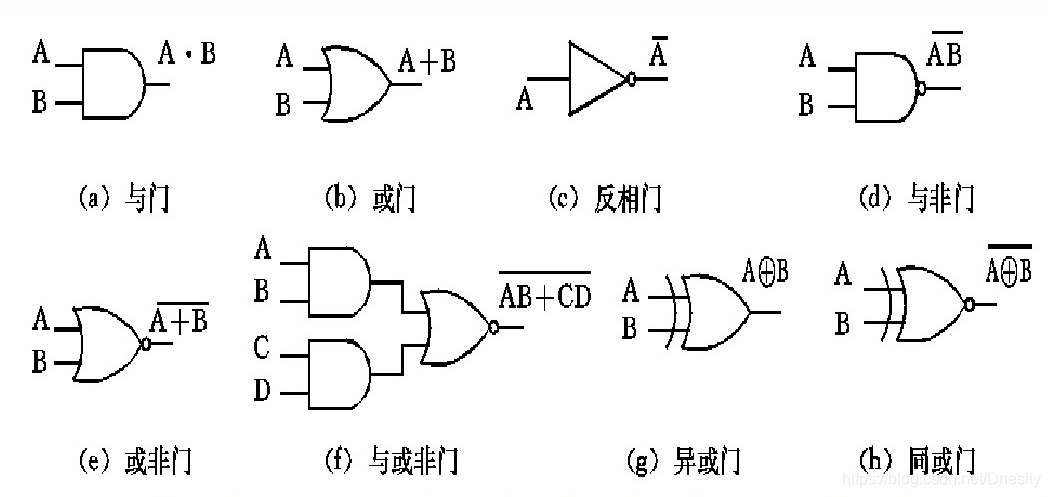
1.一位全加器

常用的全加器逻辑电路

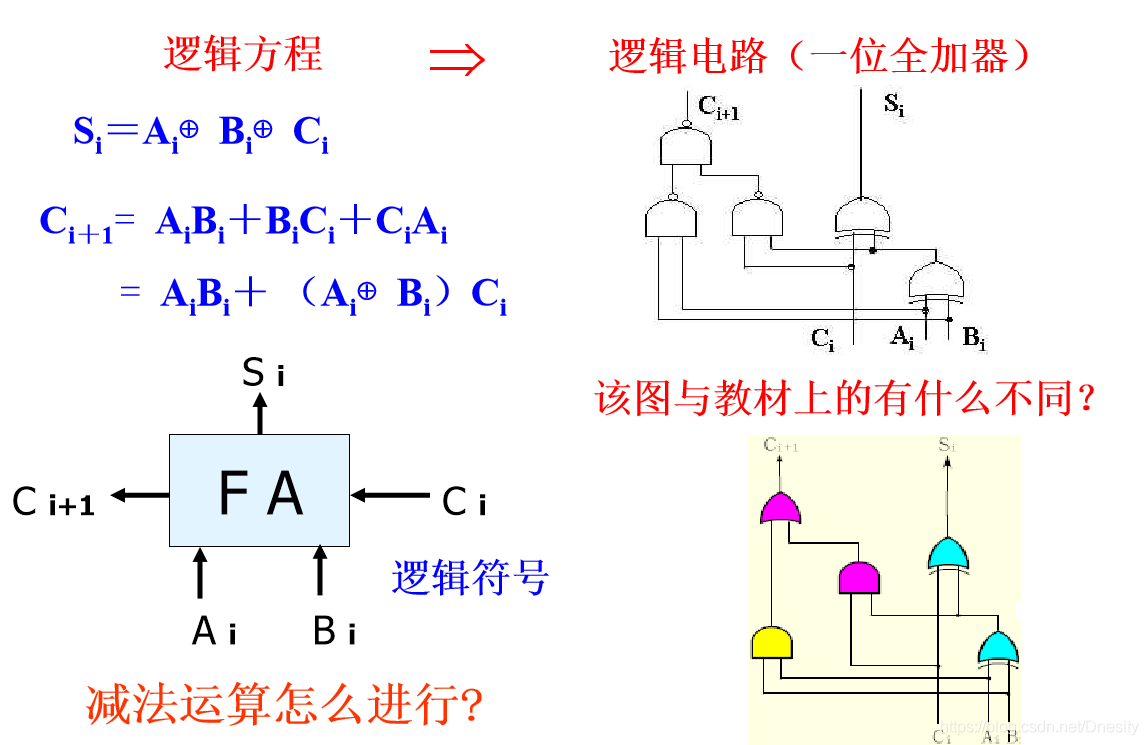
2.n位的行波进位加减器

n个1位的全加器(FA)可级联成一个n位的行波进位加减器。

行(xing)波进位:串行进位，高位的运算要等待低位的进位传到才能执行，区别于并行进位或超前进位。

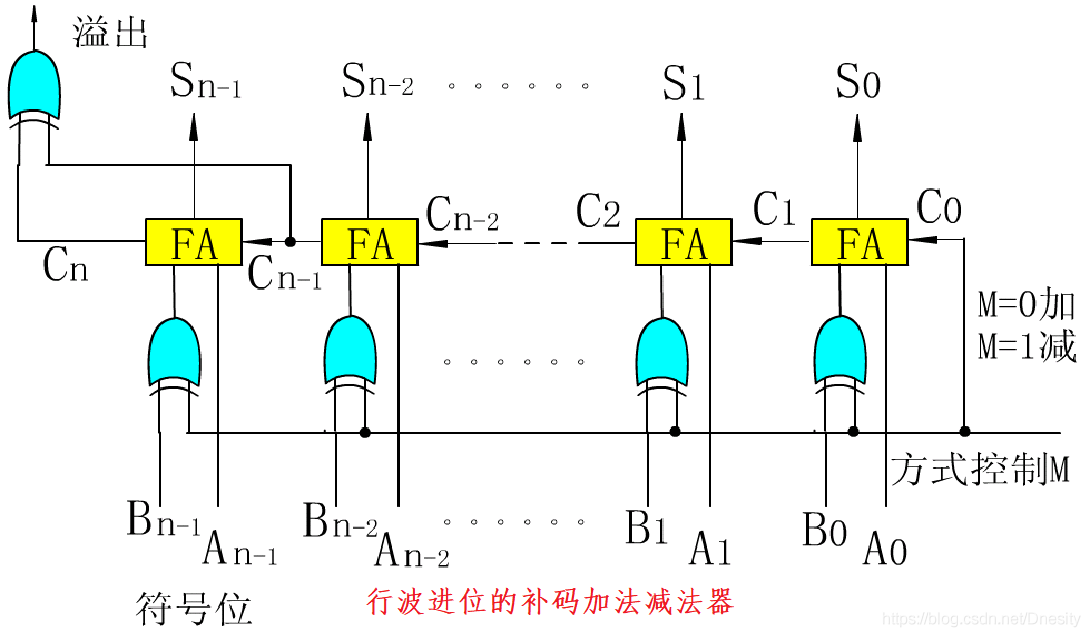
对行波进位加法/减法器的解读

1.行波进位加/减法器

n个1位的全加器(FA)可级联成一个n位的行波进位加减器

2.M为方式控制输入线(控制进行加法，还是减法运算) :

当M= 0时，作加法(A+B)运算;

当M= 1时，作减法(A- B)运算;

具体地，

[A-B]补=[A]补+[-B]补

已知[B]补，通过M=1，得到[-B]补

3.电路采用单符号位法的溢出检测逻辑:

当Cn=Cn-1时,运算无溢出;

当Cn≠Cn- 1时,运算有溢出,经异或门J产生溢出信号。

4.n位行波进位加法器的延迟时间ta的计算

当前位全加和Si必须等低位进位Ci-1来到后才能进行，加法时间与位数有关。

定义T:单级逻辑电路的单位门延迟，T通常采用一个“与非”门或一个“或非”门的时间延迟来作为度量单位。

3T:异或门的延迟时间

加法器开启之后经过3T:确定了是加运算还是减运算

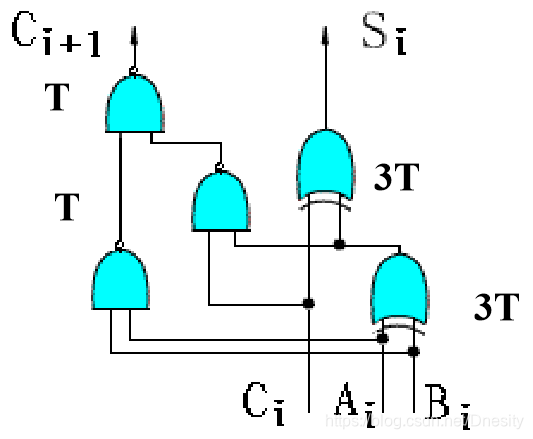
对一位全加器(FA)来说，Si的时间延迟为6T(每级异或门延迟3T)；Ci＋1的时间延迟为5T。

加法器开启之后经过6T:每个全加器Ai⊕Bi的值得到

加法器开启之后经过8T:通过C0得到了C1的值

最后一次进位完成之后，耗费3T:完成溢出检测

在整个行波进位的过程中同时得到各Si

n位行波进位加法器的延迟时间ta为:ta=3T+ 3T+ n:2T+ 3T=n.2T+9T=(2n+9)T

从上式可看出，采用行波进位加法器时，位数越多，延迟时间越长。也可采用先行进位等方法缩减运算时间。

ta为在加法器的输入端输入加数和被加数后,在最坏的情况下加法器输出端得到稳定的求和输出所需要的最长时间。

ta越小越好。

5.由一位全加器(FA)构成的行波进位加法器的缺点：

缺点：

(1)串行进位,它的运算时间长；

(2)只能完成加法和减法两种操作而不能完成逻辑操作。

多功能算术/逻辑运算单元(ALU):

不仅具有多种算术运算和逻辑运算的功能；

而且具有先行进位逻辑。

从而能实现高速运算。

二、定点乘法运算

1.乘法的手工算法

设n位被乘数和乘数用定点小数表示

被乘数 [x]原＝xf . xn－1… x1x0

乘数　[y]原＝yf . yn－1… y1y0

则乘积

[z]原＝(xf⊕yf)＋(0. xn－1… x1x0)(0. yn－1… y1y0)

式中，xf 为被乘数符号， yf 为乘数符号。

(1)乘积符号的运算规则：同号相乘为正，异号相乘为负。

(2) 手工运算过程：

设ｘ＝0.1101,ｙ＝0.1011

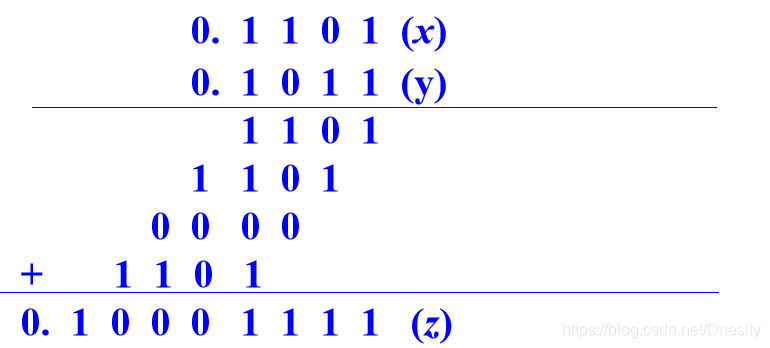
机器与人们习惯的算法不同之处：

(1) 机器通常只有n位长, 两个n位数相乘, 乘积可能为2n位。

(2) 只有两个操作数相加的加法器难以胜任将n位积一次相加起来的运算。

2.适合定点机的形式

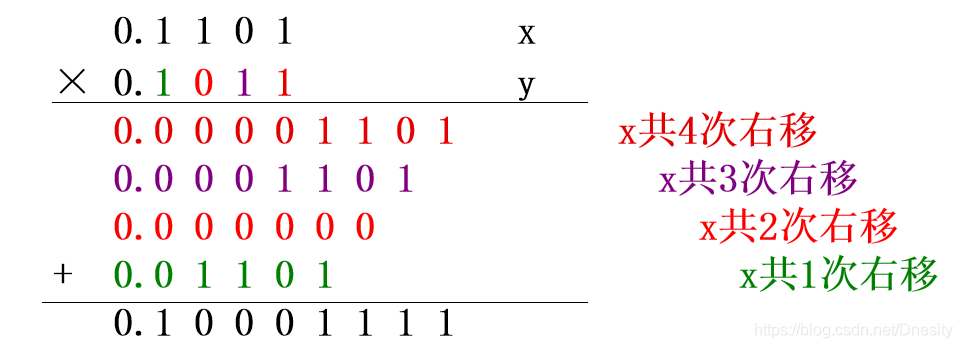
为了适合两个操作数相加的加法器，将 x·y 改写成下面形式：

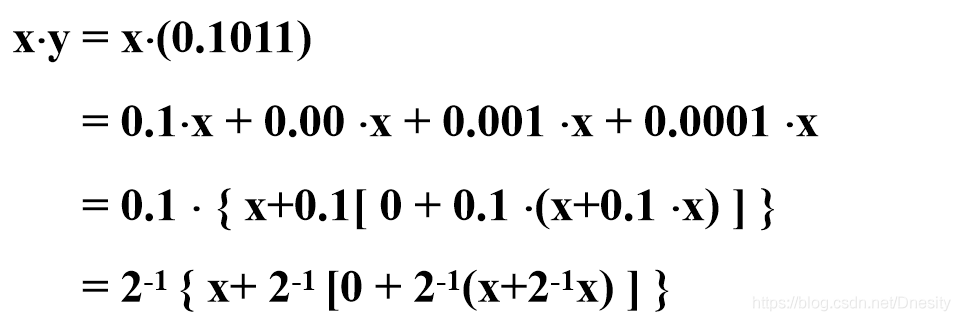
根据此式，按式中括号可表达的层次，从内向外逐次进行移位累加。

一般而言，设被乘数x,乘数y都是小于1的n位定点正数：

x=0.x1x2……xn <1

y=0.y1y2……yn <1

形成递推公式

3.原码一位乘法流程图

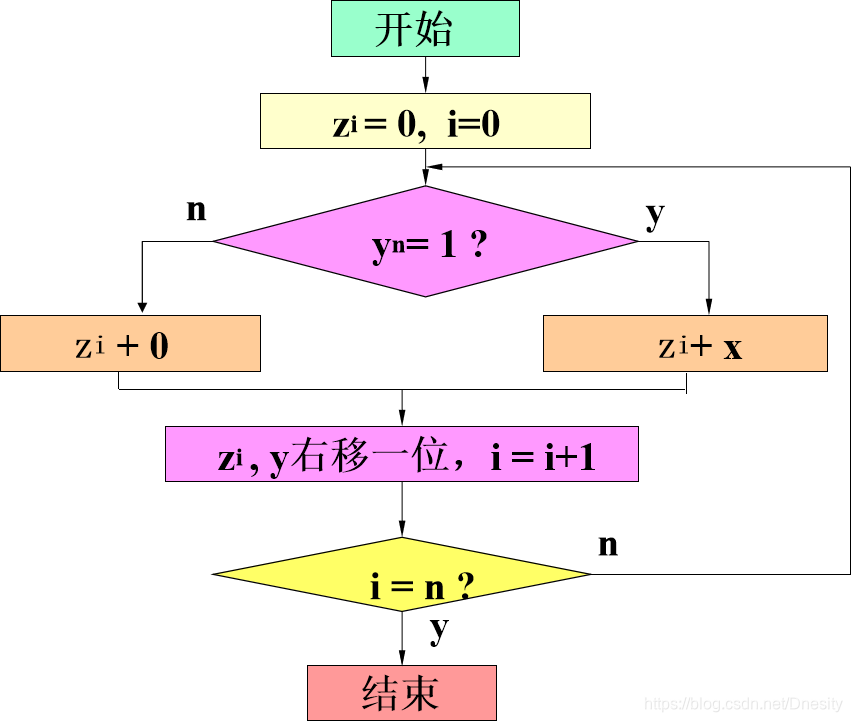
高基乘法：

以上讨论的乘法都只是检查一位二进制位。能否同时检查K位二进制位？以K=2， C=A × B为例

如果这两位二进制位为00,则加0

如果这两位二进制位为01,则加A

如果这两位二进制位为10,则加2A 2A=4A-2A

如果这两位二进制位为11,则加3A 3A=4A-A

如果这两位二进制位为11,则减A, 4A待下一次补上，由于部分积己右移两位，原来加4A变成加A号

如何知道有4A的操作?

两位二进制位为10或11，则加4A

高速乘法部件——阵列乘法器

硬件乘法器的常规设计是适用“串行移位”和“并行加法”相结合的方法

，这种方法并不需要很多器件。

然而串行方法毕竟太慢，执行一次乘法的时间至少是执行一次加法时间的n倍，

不能满足科学技术对高速乘法所提出的要求。自从大规模集成电路问世以来，高速的单元阵列乘法器应运而生，出现了各种形式的

流水线阵列乘法器

，它们属于并行乘法器，提供了极快的速度。阵列乘法器的运算过程如下：

第一：当乘数的位数字为1 时,我们可以将被乘数的值直接放置适当的位置。而适当的位置是依乘数的第几个位和被乘数做运算之后所放的位置。

第二：当乘数的位数字为0 时，我们可以将0 放置适当的位置, 以作为部分乘积。

第三：我们利用笔和纸计算的乘法，在硬件中使用与门来实现。例如：1000 ×1中，乘数1 和每一个被乘数的位都个别做与运算,其结果为1000 正是我们所要的结果。由此可知我们只需用与门就可以完成我们所要的乘法。

第四：当部分乘积都运算完成后，使用加法来完成最终的乘法结果运算。

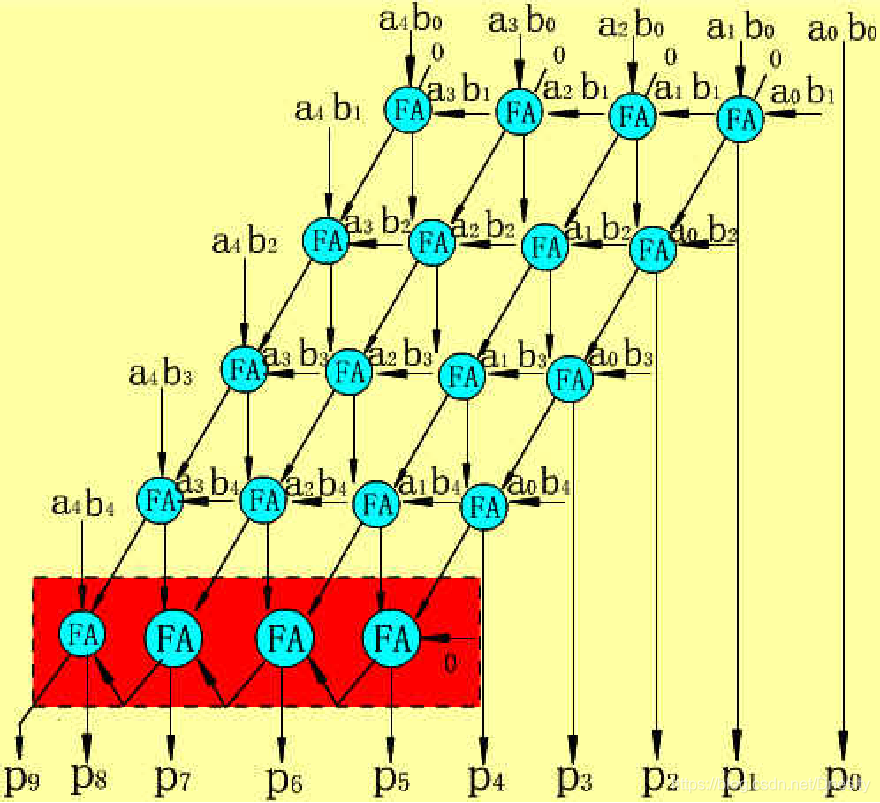
根据以上四点的说明，我们可以运用最简单、最直观的方式来描述固定点乘法器的电路描述。我们使用与门来做部分积运算，使用全加器(Full adder)来运算部分积的最终结果。图1所示为有符号位的5×5固定点乘法器的架构图。

1.串行加法器的优劣分析

• 不需要很多器件，硬件结构简单；

• 速度太慢，执行一次乘法操作的时间至少是加法操作的n倍；

由于乘法操作大约占全部算术运算的1/3，故采用高速乘法部件是非常必要的。

2.不带符号的阵列乘法器

设有两个不带符号的二进制整数 A＝am-1…a1a0 , B＝bn－1…b1b0

它们的数值分别为a和b,即：

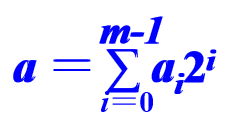
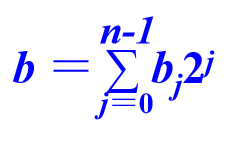
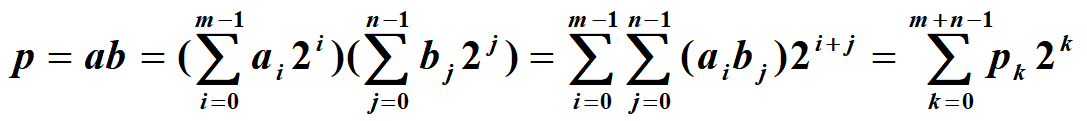
(1) 习惯方法运算过程：

(2) 不带符号阵列乘法器逻辑框图

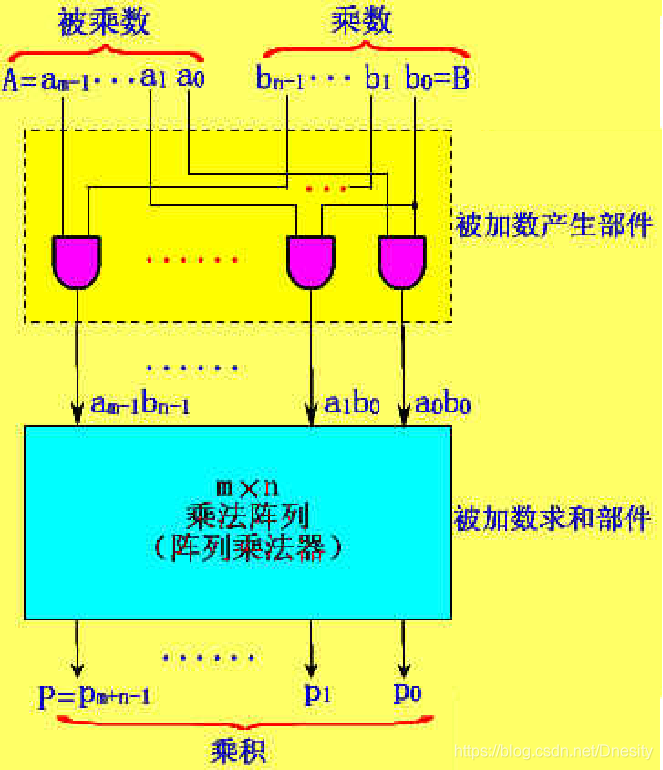
(3) 5 X 5位不带符号阵列乘法器逻辑电路图

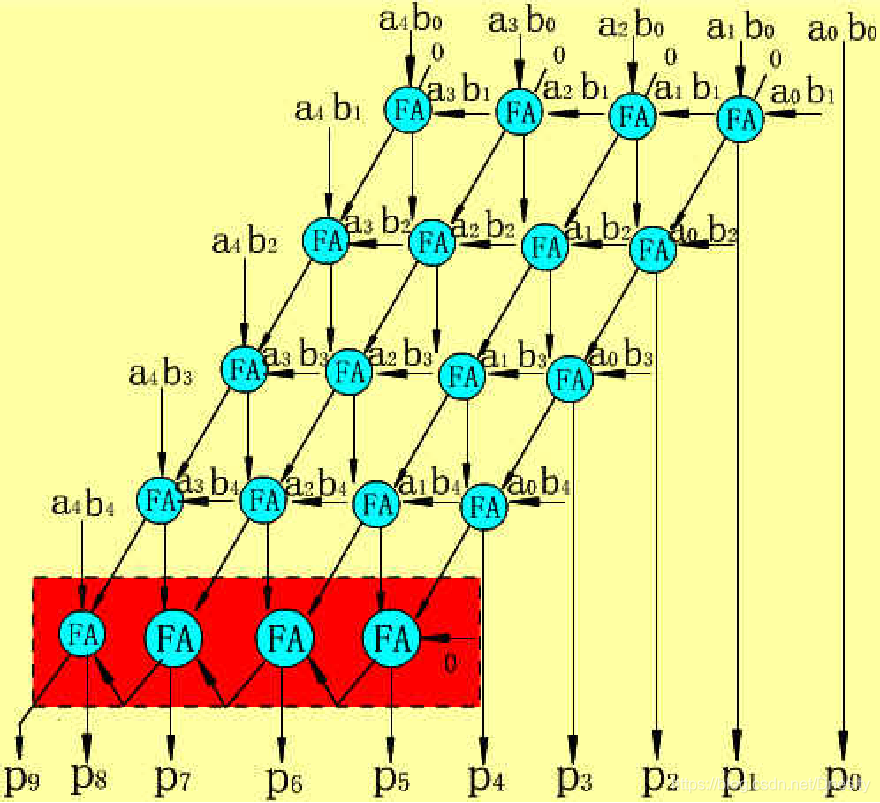
3.带符号的阵列乘法器

(1) 对2求补器电路

例1：对1010求补。

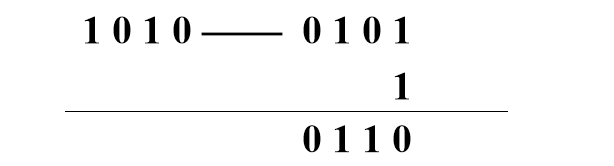
例2：对1011求补。

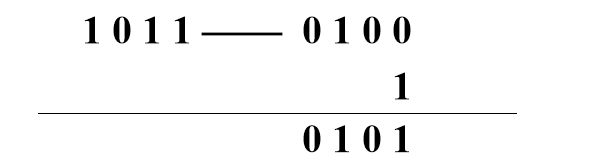
方法：

从数的最右端a0开始,由右向左, 直到找出第一个“1

”,例如ai＝1, 0≤i≤n。这样, ai以左的每一个输入位都求反, 即1变0, 0变1。

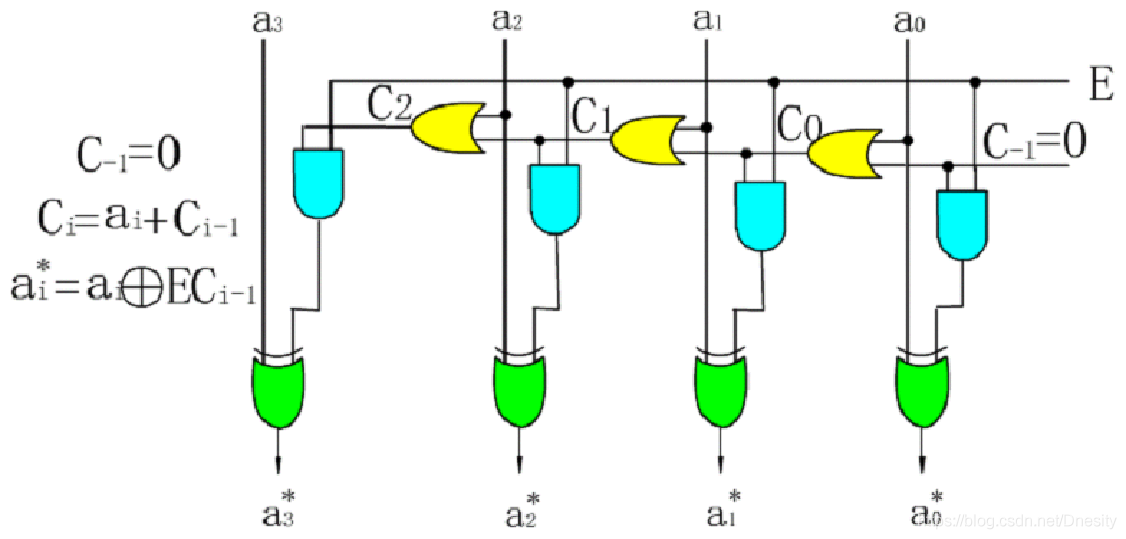
对2求补电路

(2) 带符号A的阵列乘法器

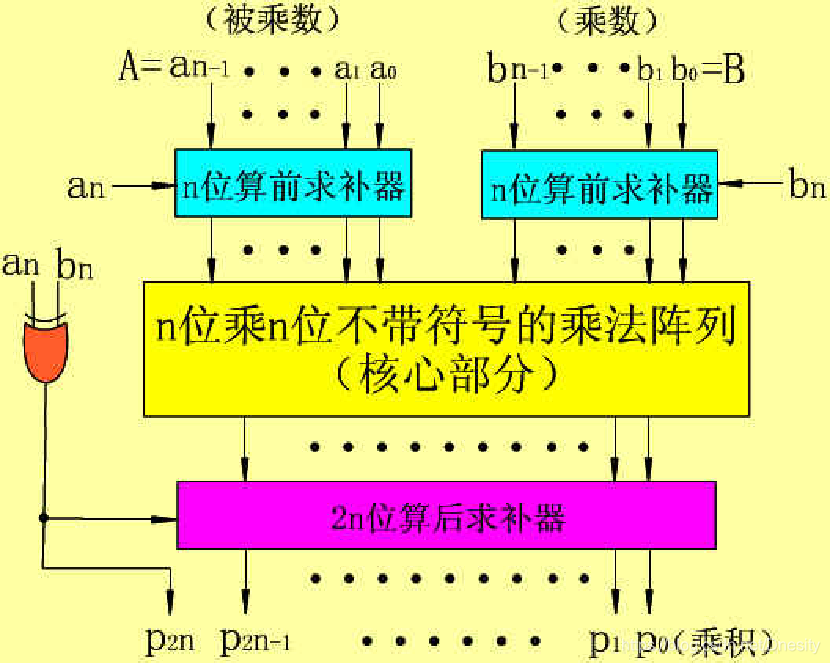
(3) 结构:

包括求补级的乘法器又称为符号求补的阵列乘法器。

在这种逻辑结构中，共使用三个求补器:

• 两个算前求补器作用是：

将两个操作数A和B在被不带符号的乘法阵列(核心部件)相乘以前，先变成正整数。

• 算后求补器作用是：

当两个输入操作数的符号不一致时,把运算结果变成带符号的数。

在必要的求补操作以后，A和B的码值输送给n×n位不带符号的阵列乘法器，并由此产生2n位的乘积:

A·B＝P＝p2n－1…p1p0 p2n＝an⊕bn 其中P2n为符号位。

三、定点除法运算

除法算法设计

设有n位定点小数：

被除数 x，其原码为　[x]原＝xf . xn－1… x1 x0

除数 y，其原码为　　[y]原＝yf . yn－1… y1 y0

则有商q＝ｘ/ｙ,其原码为 [q]原＝(xf⊕yf) + (0. xn－1…x1x0 / 0.yn－1… y1y0)

• 商的符号运算qf＝xf⊕yf 与原码乘法一样;

• 商的数值部分的运算,实质上是两个正数求商的运算。

1.手算运算步骤

例: 设被除数x=0.1001, 除数y=0.1011, 仿十进制除法运算, 手算求x÷y的过程。

得ｘ÷ｙ的商q＝0.1101, 余数为r＝0.00000001。

2.机器运算与手算的不同

原码一位除法

结果与手算相同，但余数不是真正的余数

，

多乘了2n，故正确的余数应为2-n×rn，即：0.00000001

(1) 在计算机中,小数点是固定的,不能简单地采用手算的办法。为便于机器操作,

除数Y固定不变, 被除数和余数进行左移 (相当于乘2)。

(2) 机器不会心算,必须先作减法,若余数为正, 才知道够减；若余数为负, 才知道不够减。不够减时必须恢复原来的余数, 以便再继续往下运算。这种方法称为恢复余数法。

(3) 要恢复原来的余数, 只要当前的余数加上除数即可。但由于要恢复余数, 使除法进行过程的步数不固定, 因此控制比较复杂。

实际中常用不恢复余数法,又称加减交替法。其特点是运算过程中如出现不够减,则不必恢复余数,根据余数符号, 可以继续往下运算,因此步数固定,控制简单。

3.恢复余数法

被除数减除数，够减时，商1；不够减时商0。

由于商０时若不够减，即不能作减法，但现在在判断是否商０时，已经减了除数，为了下次能正确运算，必须把已减掉的除数加回去恢复余数。这就是“

恢复余数法

”。

【例1】x=0.1001, y=0.1011, 用恢复余数法求 x/y。

解：[x]原 =[x]补= x=0.1001, [y]补=0.1011, [-y]补=1.0101

余数每次左移相当于乘以2，在求得n位商后，相当于多乘了2^n，所以最后余数应乘以2^(-n)才是正确的值。

故：[q]原=0. 1 1 0 1 余数 [r4]原=0.

0000

0001

4.加减交替法（不恢复余数法）

上述恢复余数法由于要恢复余数，使得除法的步数不固定，控制比较复杂。实际上常用的是

加减交替法。

特点：当运算过程中出现不够减的情况，不必恢复余数，而是根据余数的符号，继续往下运算，因此步数固定，控制简单。

运算规则：

当余数为正时，商1，余数左移一位，减除数；

当余数为负时，商0，余数左移一位，加除数。

【例2】x=0.1001, y=0.1011, 用加减交替法求 x/y. 解：[x]原=[x]补= x =0.1001, [y]补=0.1011, [- y]补=1.0101

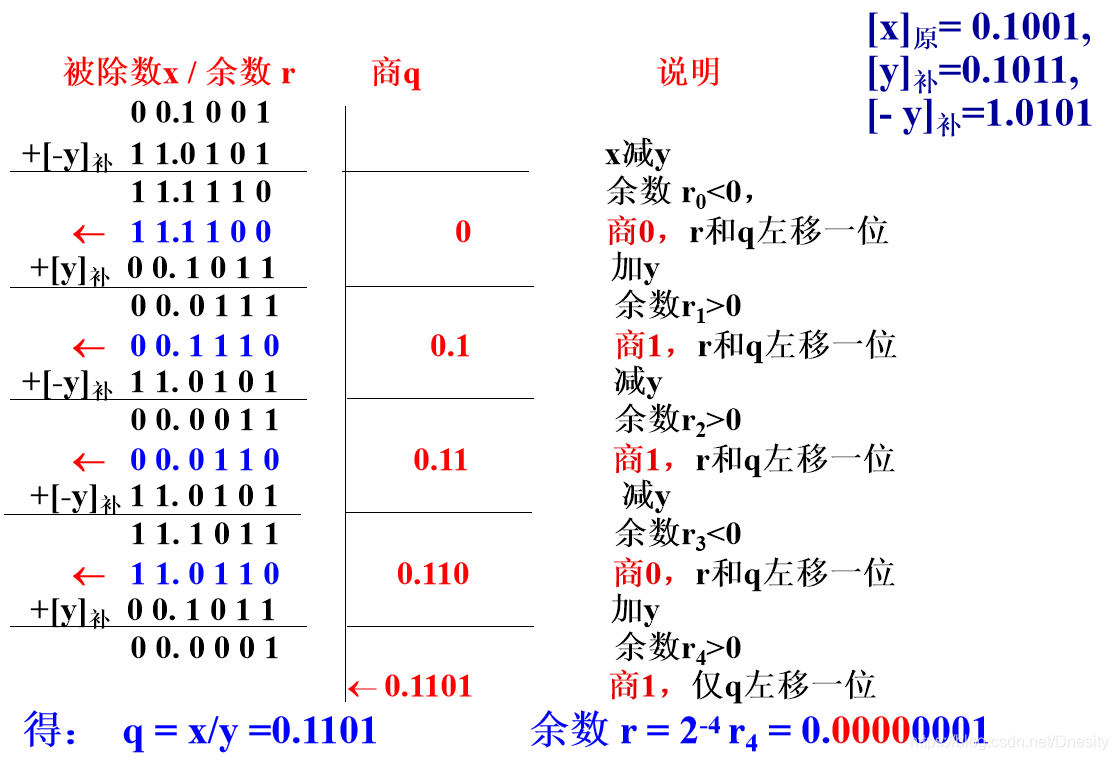
【例3】x=0.1011, y=0.1101, 用加减交替法求 x/y. 解：[x]原=[x]补= x =0.1011, [y]补=0.1101, [- y]补=1.0011

原码加减交替除法流程图

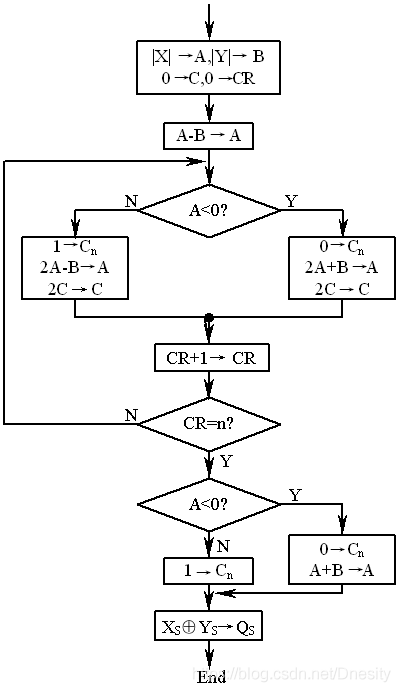
原码加减交替法原理逻辑框图

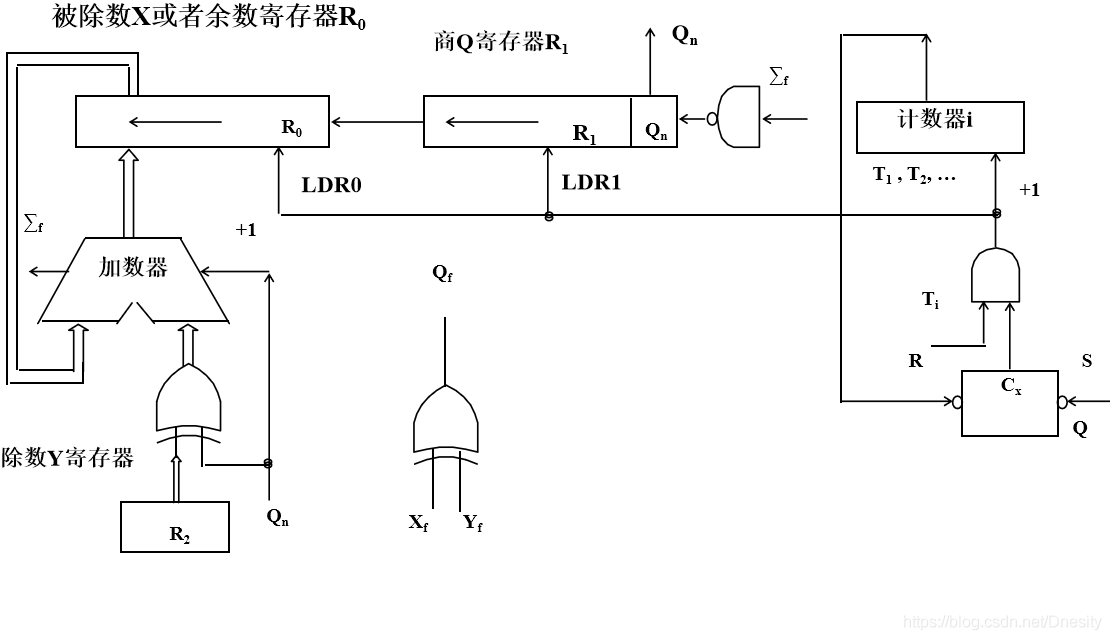
阵列除法器

阵列式除法器是一种并行运算部件, 采用大规模集成电路制造。与早期的串行除法器相比, 阵列除法器不仅所需的控制线路少, 而且能提供令人满意的高速运算速度。

阵列除法器有多种多样形式：

不恢复余数阵列除法器；

补码阵列除法器等等。

1.可控加法/减法(CAS)单元

用于并行除法流水逻辑阵列中。

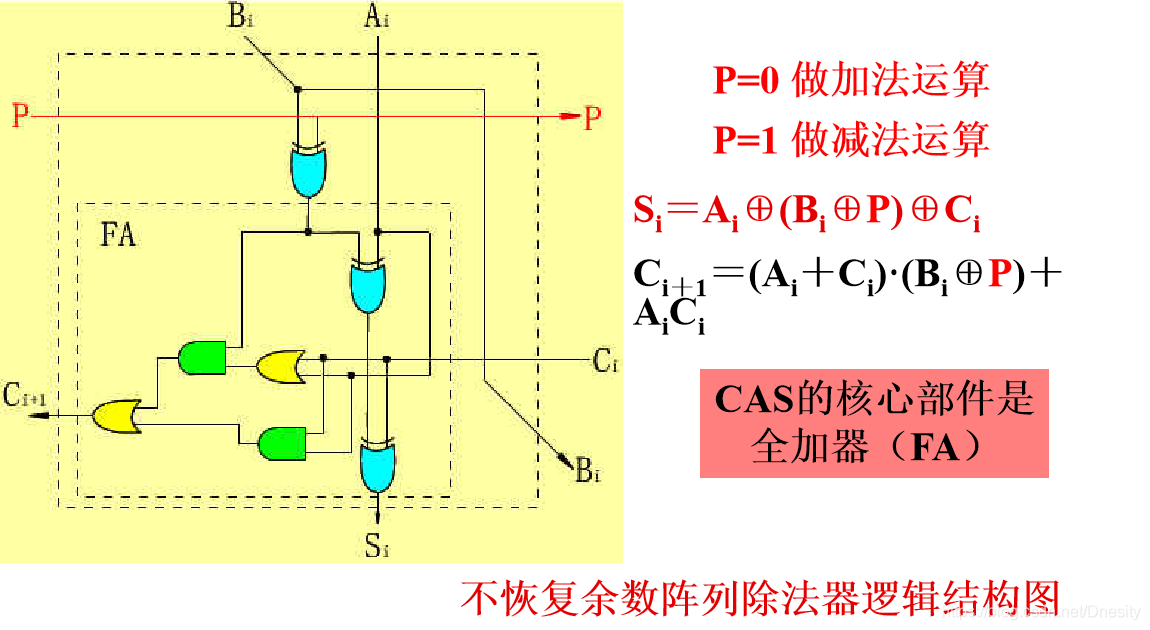
CAS单元的输入与输出的关系可用如下一组逻辑方程来表示：

Si＝Ai⊕(Bi⊕P)⊕Ci

Ci＋1＝(Ai＋Ci)·(Bi⊕P)＋AiCi

• 当P＝0时, 即是我们熟悉的一位全加器(FA)的公式：

Si＝Ai⊕Bi⊕Ci

Ci＋1＝AiBi＋BiCi＋AiCi

• 当P＝1时, 则得求差公式：

在减法情况下：输入Ci称为借位输入,而Ci＋1称为借位输出。

为说明CAS单元的实际内部电路实现,将方程式

Si＝Ai⊕(Bi⊕P)⊕Ci

Ci＋1＝(Ai＋Ci)·(Bi⊕P)＋AiCi

加以变换,可得如下形式：

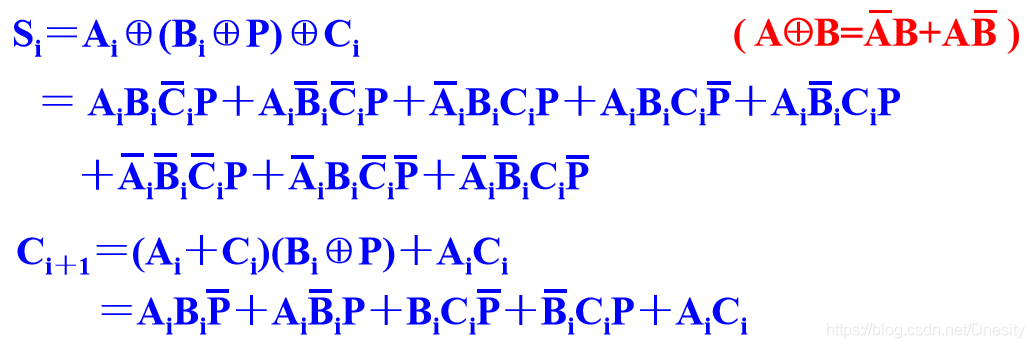
在这两个表达式中,每一个都能用一个三级组合逻辑电路(包括反向器)来实现。因此每一个基本的CAS单元的延迟时间为3T单元。

2.不恢复余数的阵列除法器（不恢复余数阵列除法，也叫加减交替法。）

在不恢复余数的除法阵列中: • 当余数为正时（ri ≥ 0) ,商“1”，下次做减法运算，减法是用2的补码运算来实现的，此时

[x-y]补= [x ]补+ [-y]补;

• 当余数为负时（ri< 0) ,商“0”，下次做加法运算;

• 每次运算完成后要将余数左移一位，再与除数做加或减运算; • 商的符号由两数的符号按位相加求得。

例： x=0.101001, y=0.111, 求x÷y。 [-y]补=1.001

例： x=0.100101, y=0.101, 求x÷y。 [-y]补=1.011

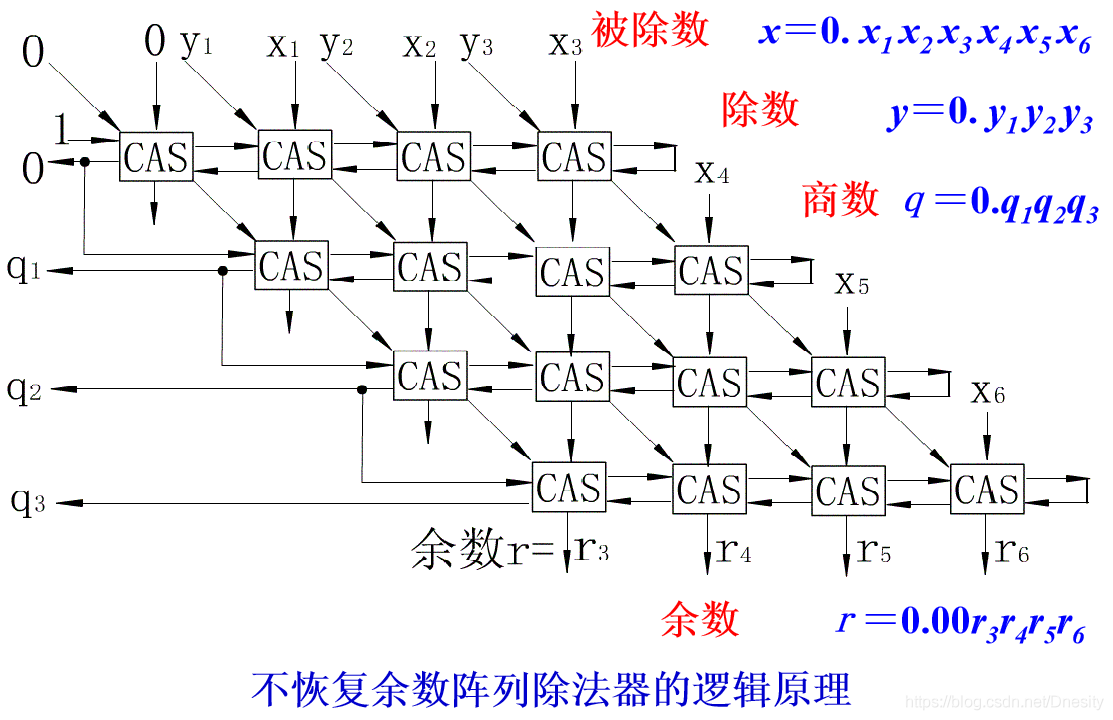
• 被除数ｘ是一个6位的小数(双倍长度值)：

ｘ＝0.ｘ1ｘ2ｘ3ｘ4ｘ5ｘ6

它是由顶部一行和最右边的对角线上的垂直输入线来提供的。

• 除数ｙ是一个3位的小数

ｙ＝0.ｙ1ｙ2ｙ3

它沿对角线方向进入这个阵列。这是因为：

在除法中所需要的部分余数的左移,可以用下列等效的操作来代替：即让余数保持固定,而将除数沿对角线右移。

• 最上面一行所执行的初始操作经常是减法。因此最上面一行的控制线P固定置成“1”。

• 减法是用2的补码运算来实现的，这时右端各CAS单元上的反馈线用作初始的进位输入。

• 每一行最左边的单元的进位输出决定着商的数值。

将当前的商反馈到下一行,我们就能确定下一行的操作。

由于进位输出信号指示出当前的部分余数的符号,因此,它将决定下一行的操作将进行加法还是减法。

由图看出,该阵列除法器是用一个可控加法/减法(CAS)单元所组成的流水阵列来实现的。

推广到一般情况：

一个(n+1) 位除(n+1)位的加减交替除法阵列由(n ＋1)2个CAS单元组成, 其中两个操作数(被除数与除数) 都是正的。 n为尾数位数。

对不恢复余数阵列除法器来说，

在进行运算时：

• 沿着每一行都有进位(或借位)传播；

• 同时所有行在它们的进位链上都是串行连接；

• 而每个CAS单元的延迟时间为3T单元。

因此，对一个2n位除以n位的不恢复余数阵列除法器来说，单元的数量为(n＋1)2，考虑最大情况下的信号延迟，其除法执行时间为

td＝3T(n＋1)^2

其中n为尾数位数。

原文链接：https://blog.csdn.net/Dnesity/article/details/104641758

你可能也喜欢