一、题目
给定一个平衡括号字符串
S
,按下述规则计算该字符串的分数:
-
()
得 1 分。 -
AB
得
A + B
分,其中 A 和 B 是平衡括号字符串。 -
(A)
得
2 * A
分,其中 A 是平衡括号字符串。
二、示例
2.1> 示例 1:
【输入】 “()”
【输出】 1
2.2> 示例 2:
【输入】 “(())”
【输出】 2
2.3> 示例 3:
【输入】 “()()”
【输出】 2
2.4> 示例 4:
【输入】 “(()(()))”
【输出】 6
提示:
-
S
是平衡括号字符串,且只含有
(
和
)
。 -
2
<= S.length <=
50
三、解题思路
根据题目描述,我们需要对字符串s进行解析,并利用堆栈的特点帮助我们进行计算。以下图为例,
s = “(()(()))”
,遍历前两个字符都是‘
(
’,所以我们将‘(’执行入栈操作。遍历到的第三个字符是‘
)
’,我们要将栈顶元素弹出,发现可以匹配成一个括号,由于题目描述,
一个“()”等于1
,所以,我们将字符‘1’入栈。此时堆栈中的元素为
['(', '1']
。具体操作如下图所示:

我们在继续遍历,由于第4和第5个字符都是‘
(
’,所以我们直接入栈即可。当遍历到第6个字符的时候,由于是‘
)
’,所以我们再次执行将栈顶元素踢出堆栈的操作,由于题目描述,
一个“()”等于1
,所以,我们将字符‘1’入栈。此时堆栈中的元素为
['(', '1','(', '1']
。具体操作如下图所示:

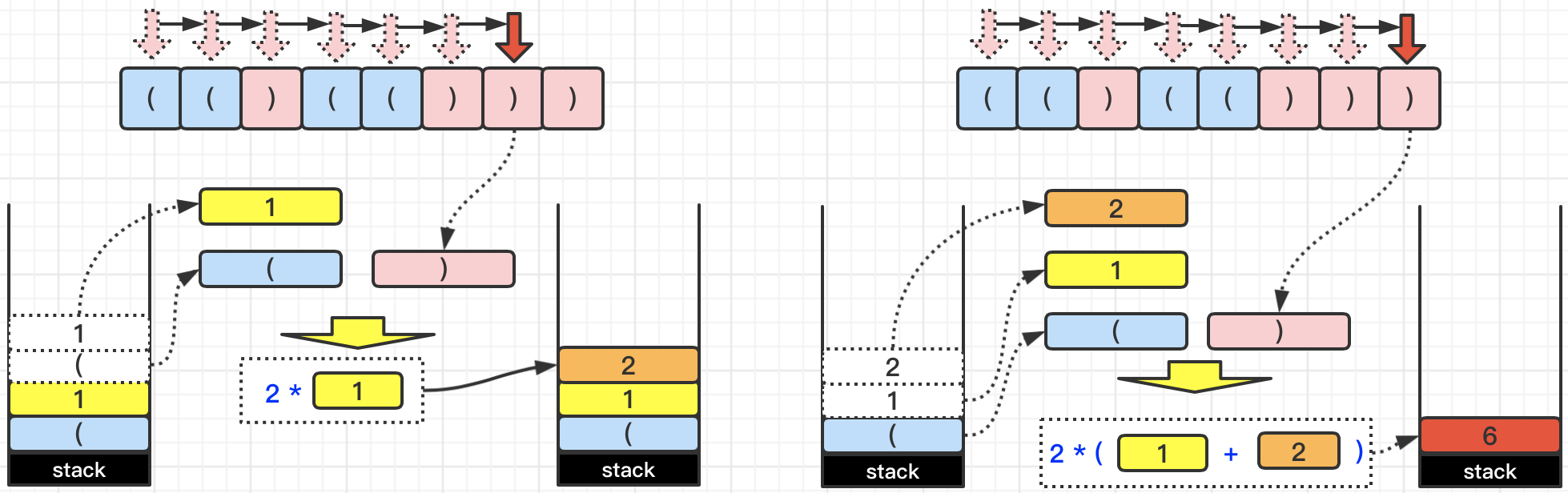
当遍历到第7个字符的时候,由于是‘
)
’,所以我们再次执行将栈顶元素踢出堆栈的操作,由于出栈的字符不是‘(’而是‘1’,所以我们继续踢出栈顶元素,此时出栈字符为‘(’,满足匹配题目中描述的
(A)
得
2 * A
分的情况,所以计算出来的结果为
2*1
等于2,我们将字符‘2’入栈。此时堆栈中的元素为
['(', '1','2']
。
我们在继续向后遍历,由于第8个字符是‘
)
’,我们执行栈顶元素出栈操作,由于栈顶和次栈顶元素分别是‘
2
’和‘
1
’,都不是‘(’,所以继续执行栈顶出栈操作。然后这次出栈的元素是‘(’,可以匹配成一个括号,同时也满足了题目中描述的
AB 得 A + B 分
和
(A) 得 2 * A 分
这两种情况。所以,计算结果为:
2 * (1 + 2)
等于 6,在将6入栈。此时堆栈中的元素为
['6']
。那么遍历s字符串完毕之后,我们将堆栈中所有元素值相加就是最终结果。具体操作,如下图所示:
四、代码实现
class Solution {
public int scoreOfParentheses(String s) {
Deque<Character> deque = new ArrayDeque();
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') deque.addLast('(');
else {
char c = deque.removeLast();
if (c == '(') {
deque.addLast('1');
} else {
int sum = c - '0';
while ((c = deque.removeLast()) != '(') sum += c - '0';
deque.addLast((char) ((sum << 1) + '0'));
}
}
}
int result = 0;
while (!deque.isEmpty()) result += deque.removeLast() - '0';
return result;
}
}

今天的文章内容就这些了:
写作不易,笔者几个小时甚至数天完成的一篇文章,只愿换来您几秒钟的
点赞
&
分享
。
更多技术干货,欢迎大家关注公众号“
爪哇缪斯
” ~ \(^o^)/ ~ 「干货分享,每天更新」