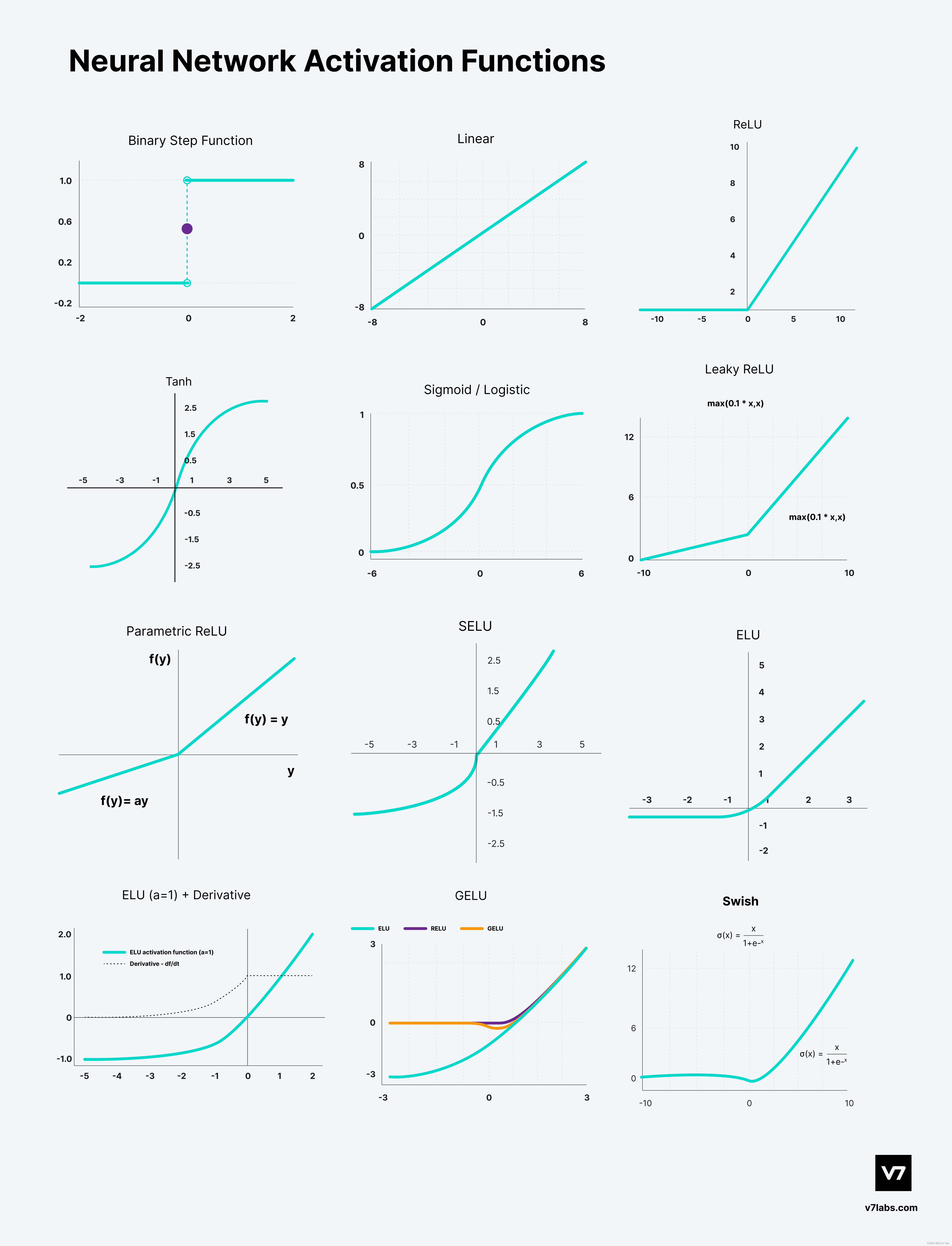

The role of activation functions
The purpose of an activation function is to add
non-linearity
to the neural network.
Let’s suppose we have a neural network working
without
the activation functions.
In that case, every neuron will only be performing a linear transformation on the inputs using the weights and biases. It’s because it doesn’t matter how many hidden layers we attach in the neural network; all layers will behave in the same way because the composition of two linear functions is a linear function itself.
Although the neural network becomes simpler, learning any complex task is impossible, and our model would be just a linear regression model.
Non-linear activation functions solve the following limitations of linear activation functions:
- They allow backpropagation because now the derivative function would be related to the input, and it’s possible to go back and understand which weights in the input neurons can provide a better prediction. 非线性激活函数支持梯度反向传播。
- They allow the stacking of multiple layers of neurons as the output would now be a non-linear combination of input passed through multiple layers. Any output can be represented as a functional computation in a neural network. 非线性激活函数使得网络的堆叠变得有意义,对于线性激活函数而言,网络只能学习到线性变换,也就是说,网络的堆叠没有意义。
1.
Sigmoid
/ Logistic Activation Function
Sigmoid

This function takes any real value as input and outputs values in the range of 0 to 1.
Sigmoid
function
σ
(
x
)
=
1
1
+
e
−
x
\sigma(x)=\frac{1}{1+e^{-x}}
σ
(
x
)
=
1
+
e
−
x
1
The derivative of
Sigmoid
function
σ
′
(
x
)
=
σ
(
x
)
(
1
−
σ
(
x
)
)
\sigma ‘(x)=\sigma(x)(1-\sigma(x))
σ
′
(
x
)
=
σ
(
x
)
(
1
−
σ
(
x
)
)
Advantages of
Sigmoid
Function
It is commonly used for models where we have to predict the probability as an output. Since probability of anything exists only between the range of 0 and 1, sigmoid is the right choice because of its range.
The function is differentiable and provides a smooth gradient, i.e., preventing jumps in output values. This is represented by an S-shape of the sigmoid activation function.
Limitation of
Sigmoid
function
-
梯度消失 It implies that for values greater than 3 or less than -3, the function will have very small gradients. As the gradient value approaches zero, the network ceases to learn and suffers from the
Vanishing gradient
problem. -
计算效率低 ( 与
ReLU
等函数对比)
2.
Tanh
Function (Hyperbolic Tangent)
Tanh

Tanh
激活函数
tanh
(
x
)
=
(
e
x
−
e
−
x
)
(
e
x
+
e
−
x
)
\text{tanh}(x)=\frac{\left(e^{x}-e^{-x}\right)}{\left(e^{x}+e^{-x}\right)}
tanh
(
x
)
=
(
e
x
+
e
−
x
)
(
e
x
−
e
−
x
)
Advantages of
Tanh
Function
- The output of the tanh activation function is Zero centered; hence we can easily map the output values as strongly negative, neutral, or strongly positive.
- Usually used in hidden layers of a neural network as its values lie between -1 to; therefore, the mean for the hidden layer comes out to be 0 or very close to it. It helps in centering the data and makes learning for the next layer much easier.
Limitation of
Tanh
function
- it also faces the problem of vanishing gradients similar to the sigmoid activation function.
3.
ReLU
Function / Rectified Linear Unit
ReLU

ReLU
激活函数
f
(
x
)
=
max
(
0
,
x
)
f(x)=\max (0, x)
f
(
x
)
=
max
(
0
,
x
)
Advantages of
ReLU
Function
-
Since only a certain number of neurons are activated, the ReLU function is far more
computationally efficient
when compared to the sigmoid and tanh functions. -
ReLU accelerates the convergence of gradient descent towards the global minimum of the loss function due to its linear,
non-saturating
property.
Limitation of
ReLU
function
- All the negative input values become zero immediately, which decreases the model’s ability to fit or train from the data properly.
4.
Leaky ReLU
Function
Leaky ReLU
Leaky ReLU
激活函数
f
(
x
)
=
max
(
0.1
x
,
x
)
f(x)=\max (0.1x, x)
f
(
x
)
=
max
(
0
.
1
x
,
x
)
Leaky ReLU is an improved version of ReLU function to solve the Dying ReLU problem as it has a small positive slope in the negative area.
Limitation of
Leaky ReLU
function
- The predictions may not be consistent for negative input values.
-
The gradient for negative values is a small value that
makes the learning of model parameters time-consuming
.
5.
Parametric ReLU
Function
Parametric ReLU
f
(
x
)
=
max
(
α
x
,
x
)
f(x)=\max (\alpha x, x)
f
(
x
)
=
max
(
α
x
,
x
)
Parametric ReLU is another variant of ReLU that aims to solve the problem of gradient’s becoming zero for the left half of the axis.
This function provides the slope of the negative part of the function as an argument
a
. By performing backpropagation, the most appropriate value of
α
\alpha
α
is learnt.
Where
α
\alpha
α
is the slope parameter for negative values.
The parameterized ReLU function is used when the leaky ReLU function still fails at solving the problem of dead neurons, and the relevant information is not successfully passed to the next layer.
This function’s limitation is that it may perform differently for different problems depending upon the value of slope parameter
α
\alpha
α
.
6. Exponential Linear Units (
ELUs
) Function
ELUs

f
(
x
)
=
{
x
for
x
⩾
0
α
(
e
x
−
1
)
for
x
<
0
f(x)=\begin{cases}x & \text { for } x \geqslant 0 \\ \alpha\left(e^{x}-1\right) & \text { for } x<0\end{cases}
f
(
x
)
=
{
x
α
(
e
x
−
1
)
for
x
⩾
0
for
x
<
0
Advantages of
ELU
Function
-
ELU becomes smooth slowly until its output equal to
−α
-\alpha
−
α
whereas ReLU sharply smoothes. - Avoids dead ReLU problem by introducing log curve for negative values of input. It helps the network nudge weights and biases in the right direction.
Limitation of
ELU
function
- It increases the computational time because of the exponential operation included
-
No learning of the
α\alpha
α
value takes place - Exploding gradient problem
7.
Softmax
Function
Softmax
Softmax
activation function make things easy for multi-class classification problems.
8.
Swish
Swish
It is a
self-gated activation function
developed by researchers at Google.

f
(
x
)
=
x
∗
sigmoid
(
x
)
f(x)=x * \operatorname{sigmoid}(x)
f
(
x
)
=
x
∗
s
i
g
m
o
i
d
(
x
)
Here are a few advantages of the Swish activation function over
ReLU
:
-
Swish is a smooth function that means that it does not abruptly change direction like
ReLU
does near x = 0. Rather, it smoothly bends from 0 towards values < 0 and then upwards again. -
Small negative values were zeroed out in
ReLU
activation function. However, those negative values may still be relevant for capturing patterns underlying the data. Large negative values are zeroed out for reasons of sparsity making it a win-win situation. -
The swish function being non-monotonous enhances the expression of input data and weight to be learnt.
9. Gaussian Error Linear Unit (
GELU
)
GELU

f
(
x
)
=
x
P
(
X
≤
x
)
=
x
Φ
(
x
)
=
0.5
x
(
1
+
tanh
[
2
/
π
(
x
+
0.044715
x
3
)
]
)
\begin{gathered} f(x)=x P(X \leq x)=x \Phi(x) \\ =0.5 x\left(1+\tanh \left[\sqrt{2 / \pi}\left(x+0.044715 x^{3}\right)\right]\right) \end{gathered}
f
(
x
)
=
x
P
(
X
≤
x
)
=
x
Φ
(
x
)
=
0
.
5
x
(
1
+
tanh
[
2
/
π
(
x
+
0
.
0
4
4
7
1
5
x
3
)
]
)
The Gaussian Error Linear Unit (
GELU
) activation function is compatible with BERT, ROBERTa, ALBERT, and other top NLP models. This activation function is motivated by combining properties from dropout, zoneout, and
ReLUs
.
GELU
nonlinearity is better than
ReLU
and
ELU
activations and finds performance improvements across all tasks in domains of
computer vision
, natural language processing, and speech recognition.
10. Scaled Exponential Linear Unit (
SELU
)
SELU
SELU
was defined in
self-normalizing
networks and takes care of internal normalization which means each layer preserves the mean and variance from the previous layers.
SELU
enables this normalization by adjusting the mean and variance.
SELU
has both positive and negative values to shift the mean, which was impossible for
ReLU
activation function as it cannot output negative values.
Gradients can be used to adjust the variance. The activation function needs a region with a gradient larger than one to increase it.

f
(
α
,
x
)
=
λ
{
α
(
e
x
−
1
)
for
x
<
0
x
for
x
⩾
0
f(\alpha, x)=\lambda \begin{cases}\alpha\left(e^{x}-1\right) & \text { for } x<0 \\ x & \text { for } x \geqslant 0\end{cases}
f
(
α
,
x
)
=
λ
{
α
(
e
x
−
1
)
x
for
x
<
0
for
x
⩾
0
SELU
has values of alpha α and lambda λ predefined.
Here’s the main advantage of
SELU
over
ReLU
:
-
Internal normalization
is faster than external normalization, which means the network converges faster.
SELU
is a relatively newer activation function and needs more papers on architectures such as CNNs and RNNs, where it is comparatively explored.
Why are deep neural networks hard to train?
There are two challenges you might encounter when training your deep neural networks.
Vanishing Gradients
Like the sigmoid function, certain activation functions squish an ample input space into a small output space between 0 and 1.
Therefore, a large change in the input of the sigmoid function will cause a small change in the output. Hence, the derivative becomes small. For shallow networks with only a few layers that use these activations, this isn’t a big problem.
However, when more layers are used, it can cause the gradient to be too small for training to work effectively.
Exploding Gradients
Exploding gradients are problems where significant error gradients accumulate and result in very large updates to neural network model weights during training.
An unstable network can result when there are exploding gradients, and the learning cannot be completed.
The values of the weights can also become so large as to overflow and result in something called NaN values.
How to choose the right Activation Function?
You need to match your activation function for your output layer based on the type of prediction problem that you are solving—specifically, the type of predicted variable.
Here’s what you should keep in mind.
As a rule of thumb, you can begin with using the ReLU activation function and then move over to other activation functions if ReLU doesn’t provide optimum results.
And here are a few other guidelines to help you out.
- ReLU activation function should only be used in the hidden layers.
- Sigmoid/Logistic and Tanh functions should not be used in hidden layers as they make the model more susceptible to problems during training (due to vanishing gradients).
- Swish function is used in neural networks having a depth greater than 40 layers.
Finally, a few rules for choosing the activation function for your output layer based on the type of prediction problem that you are solving:
-
Regression
– Linear Activation Function -
Binary Classification
—Sigmoid/Logistic Activation Function -
Multiclass Classification
—Softmax -
Multilabel Classification
—Sigmoid
The activation function used in hidden layers is typically chosen based on the type of neural network architecture.
-
Convolutional Neural Network (CNN)
: ReLU activation function. -
Recurrent Neural Network
: Tanh and/or Sigmoid activation function.
参考资料:
[1]
12 Types of Neural Networks Activation Functions: How to Choose? (v7labs.com)