罗德里格斯公式推导
第一部分
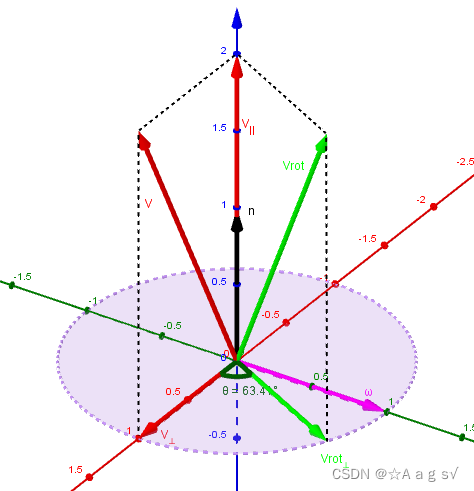
向量
v
=
(
v
x
,
v
y
,
v
z
)
T
v=(v_{x},v_{y},v_{z})^{T}
v
=
(
v
x
,
v
y
,
v
z
)
T
绕
单位
方向矢量
n
=
(
n
x
,
n
y
,
n
z
)
T
n=(n_{x},n_{y},n_{z})^{T}
n
=
(
n
x
,
n
y
,
n
z
)
T
转过角度
θ
\theta
θ
得到向量
v
r
o
t
v_{rot}
v
ro
t
.
v
∣
∣
=
(
v
⋅
n
)
n
w
=
(
n
×
v
)
v
⊥
=
v
−
v
∣
∣
=
v
−
(
v
⋅
n
)
n
v
⊥
=
−
n
×
w
=
−
n
×
(
n
×
v
)
v
∣
∣
=
v
+
n
×
(
n
×
v
)
v_{||}=(v \cdot n)n\\ w= (n\times v)\\ v_{\perp}=v-v_{||}=v-(v \cdot n)n\\ v_{\perp}=-n\times w = -n\times (n\times v)\\ v_{||}=v+n\times (n\times v)
v
∣∣
=
(
v
⋅
n
)
n
w
=
(
n
×
v
)
v
⊥
=
v
−
v
∣∣
=
v
−
(
v
⋅
n
)
n
v
⊥
=
−
n
×
w
=
−
n
×
(
n
×
v
)
v
∣∣
=
v
+
n
×
(
n
×
v
)
n
×
v
=
∣
i
j
k
n
x
n
y
n
z
v
x
v
y
v
z
∣
=
[
0
−
n
z
n
y
n
z
0
−
n
x
−
n
y
n
x
0
]
[
v
x
v
y
v
z
]
=
N
v
=
n
×
v
n\times v\ =\ \left|\begin{array}{ccc}\boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ n_x & n_y & n_z \\ v_x & v_y & v_z \end{array}\right| = \ \left[\begin{array}{ccc} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{array}\right] \left[\begin{array}{c}v_x \\ v_y \\ v_z \end{array}\right]\ = \ Nv\ =\ n^{\times}v
n
×
v
=
i
n
x
v
x
j
n
y
v
y
k
n
z
v
z
=
0
n
z
−
n
y
−
n
z
0
n
x
n
y
−
n
x
0
v
x
v
y
v
z
=
N
v
=
n
×
v
v
r
o
t
=
v
∣
∣
+
v
⊥
cos
θ
+
w
sin
θ
=
v
+
n
×
(
n
×
v
)
−
n
×
(
n
×
v
)
cos
θ
+
(
n
×
v
)
sin
θ
=
v
+
(
1
−
cos
θ
)
N
2
v
+
N
v
sin
θ
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
=
R
v
\begin{aligned} v_{rot}&=v_{||}+v_{\perp}\cos \theta +w\sin \theta \\ &=v+n\times (n\times v) -n\times (n\times v)\cos \theta +(n\times v)\sin \theta \\ &=v+(1-\cos \theta )N^{2}v+Nv\sin \theta \\ &=[I+(1-\cos \theta )N^{2}+N\sin \theta ]v \\ &= Rv \end{aligned}
v
ro
t
=
v
∣∣
+
v
⊥
cos
θ
+
w
sin
θ
=
v
+
n
×
(
n
×
v
)
−
n
×
(
n
×
v
)
cos
θ
+
(
n
×
v
)
sin
θ
=
v
+
(
1
−
cos
θ
)
N
2
v
+
N
v
sin
θ
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
=
R
v
其中
N
2
=
N
⋅
N
=
[
−
n
y
2
−
n
z
2
n
x
n
y
n
x
n
z
n
x
n
y
−
n
x
2
−
n
z
2
n
y
n
z
n
x
n
z
n
y
n
z
−
n
x
2
−
n
y
2
]
=
[
n
x
2
−
1
n
x
n
y
n
x
n
z
n
x
n
y
n
y
2
−
1
n
y
n
z
n
x
n
z
n
y
n
z
n
z
2
−
1
]
=
n
⋅
n
T
−
I
\begin{aligned} N^{2}=N\cdot N &=\left[\begin{array}{ccc} -n_{y}^{2}-n_{z}^{2} & n_{x}n_{y} & n_{x}n_{z} \\ n_{x}n_{y} & -n_{x}^{2}-n_{z}^{2} & n_{y}n_{z} \\ n_{x}n_{z} & n_{y}n_{z} & -n_{x}^{2}-n_{y}^{2} \end{array}\right]\\ &=\left[\begin{array}{ccc} n_{x}^{2}-1 & n_{x}n_{y} & n_{x}n_{z} \\ n_{x}n_{y} & n_{y}^{2}-1 & n_{y}n_{z} \\ n_{x}n_{z} & n_{y}n_{z} & n_{z}^{2}-1 \end{array}\right]\\ &= n \cdot n^{T} – I \end{aligned}
N
2
=
N
⋅
N
=
−
n
y
2
−
n
z
2
n
x
n
y
n
x
n
z
n
x
n
y
−
n
x
2
−
n
z
2
n
y
n
z
n
x
n
z
n
y
n
z
−
n
x
2
−
n
y
2
=
n
x
2
−
1
n
x
n
y
n
x
n
z
n
x
n
y
n
y
2
−
1
n
y
n
z
n
x
n
z
n
y
n
z
n
z
2
−
1
=
n
⋅
n
T
−
I
所以
R
=
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
=
I
+
(
1
−
cos
θ
)
(
n
⋅
n
T
−
I
)
+
N
sin
θ
=
I
cos
θ
+
(
1
−
cos
θ
)
n
⋅
n
T
+
N
sin
θ
\begin{aligned} R&=I+(1-\cos \theta )N^{2}+N\sin \theta \\ &=I+(1-\cos \theta )(n\cdot n^{T}-I)+N\sin \theta \\ &=I\cos \theta +(1-\cos \theta )n\cdot n^{T}+N\sin \theta \end{aligned}
R
=
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
=
I
+
(
1
−
cos
θ
)
(
n
⋅
n
T
−
I
)
+
N
sin
θ
=
I
cos
θ
+
(
1
−
cos
θ
)
n
⋅
n
T
+
N
sin
θ
第二部分
以上是向量
v
=
(
v
x
,
v
y
,
v
z
)
T
v=(v_{x},v_{y},v_{z})^{T}
v
=
(
v
x
,
v
y
,
v
z
)
T
和
单位
方向矢量
n
=
(
n
x
,
n
y
,
n
z
)
T
n=(n_{x},n_{y},n_{z})^{T}
n
=
(
n
x
,
n
y
,
n
z
)
T
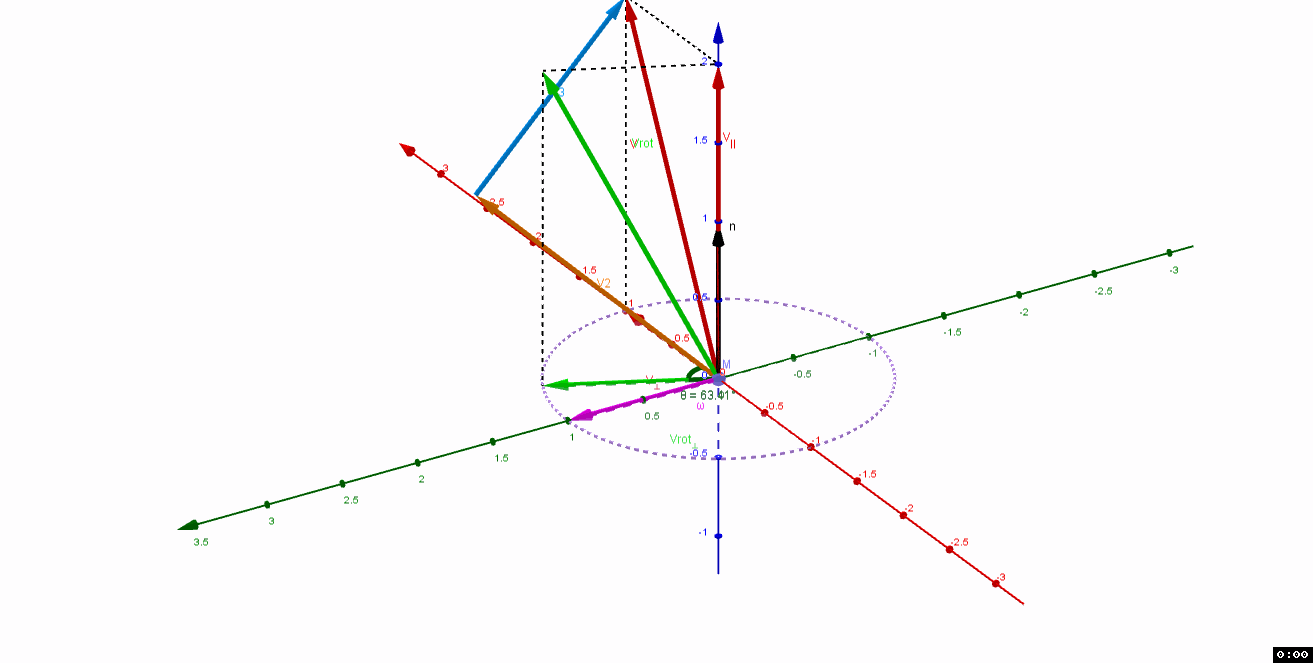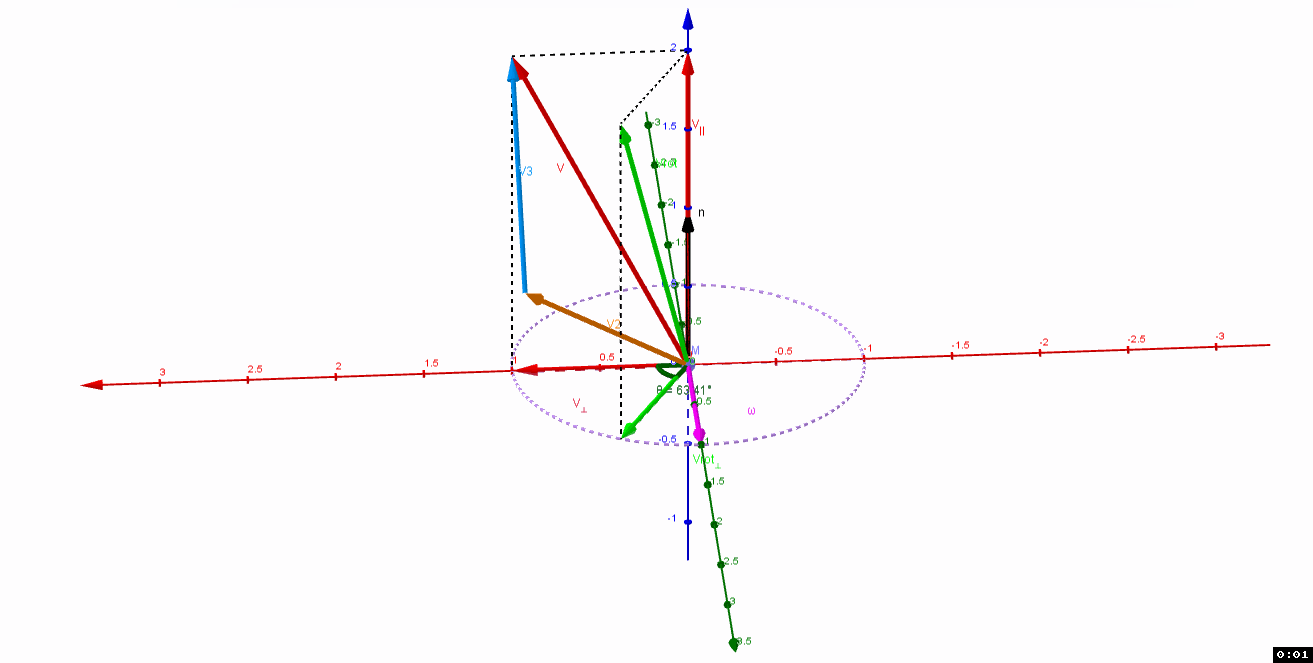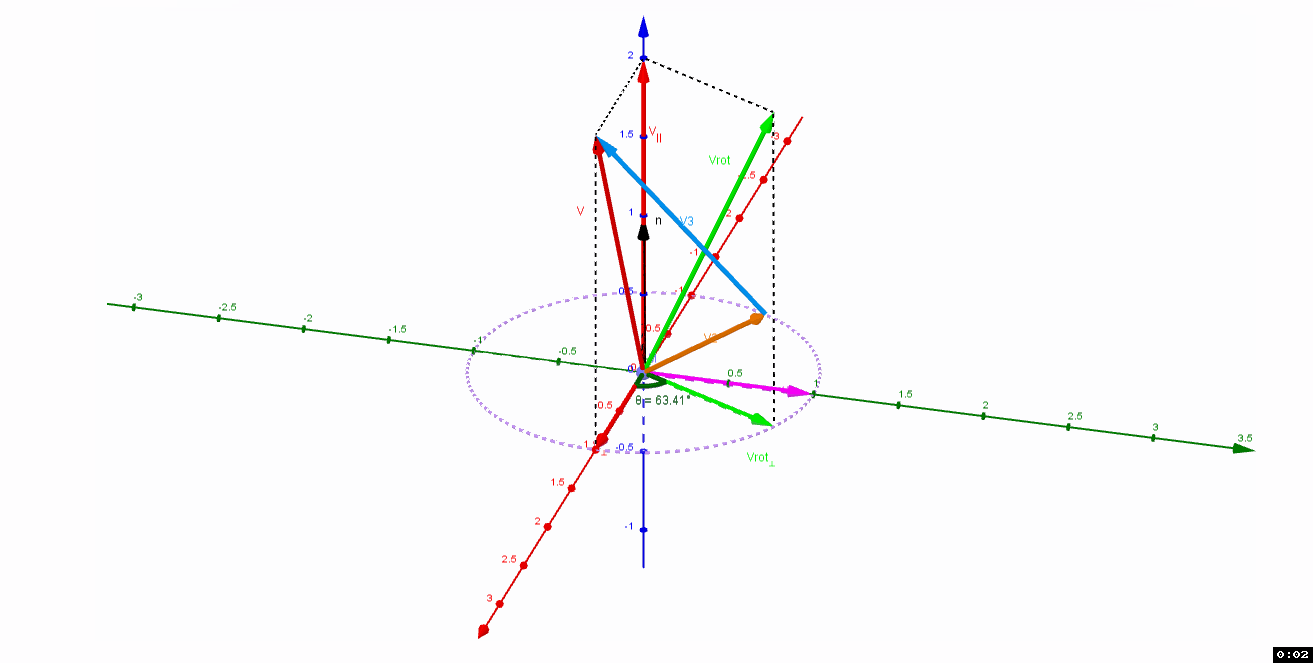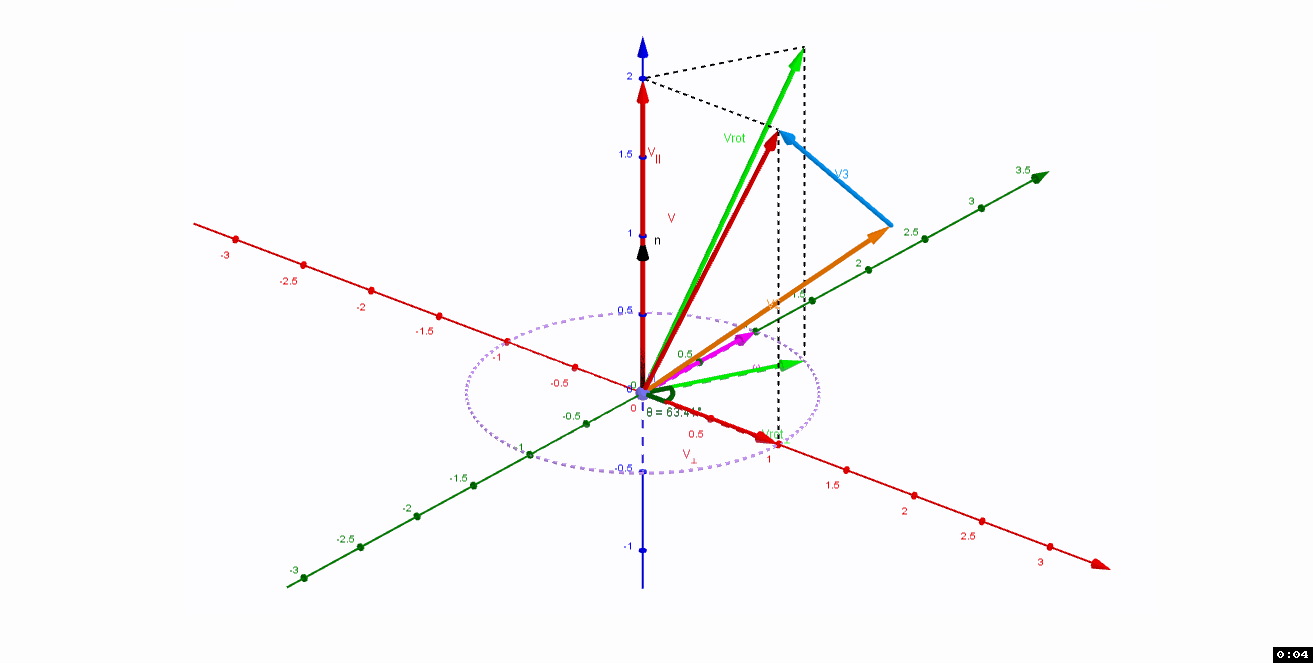
共面。如果二者不共面,如下图
v
3
v_3
v
3
,可以将
v
3
v_3
v
3
平移,使
v
3
v_3
v
3
和
n
n
n
共面再用上面公式.
或者使用
与
n
n
n
共面的
v
v
v
和
v
2
v_2
v
2
构造
v
3
v_3
v
3
,即
v
3
=
v
−
v
2
v_3=v-v_2
v
3
=
v
−
v
2
.
这里
v
v
v
和
v
2
v_2
v
2
满足
v
r
o
t
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
v
2
r
o
t
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
2
\begin{aligned} v_{rot}&=[I+(1-\cos \theta )N^{2}+N\sin \theta ]v \\ v_{2rot}&=[I+(1-\cos \theta )N^{2}+N\sin \theta ]v_{2} \end{aligned}
v
ro
t
v
2
ro
t
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
2
所以向量
v
3
v_3
v
3
绕
单位
方向矢量
n
=
(
n
x
,
n
y
,
n
z
)
T
n=(n_{x},n_{y},n_{z})^{T}
n
=
(
n
x
,
n
y
,
n
z
)
T
转过角度
θ
\theta
θ
得到向量
v
3
r
o
t
v_{3rot}
v
3
ro
t
的公式如下:
v
3
r
o
t
=
v
r
o
t
−
v
2
r
o
t
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
(
v
−
v
2
)
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
3
\begin{aligned} v_{3rot}&=v_{rot}-v_{2rot}\\ &=[I+(1-\cos \theta )N^{2}+N\sin \theta ](v-v_2)\\ &=[I+(1-\cos \theta )N^{2}+N\sin \theta ]v_3 \end{aligned}
v
3
ro
t
=
v
ro
t
−
v
2
ro
t
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
(
v
−
v
2
)
=
[
I
+
(
1
−
cos
θ
)
N
2
+
N
sin
θ
]
v
3
由上可知:即使
v
3
v_3
v
3
和
n
n
n
不共面,仍然满足罗德里格斯公式,因为这个空间是线性的.