最近写论文遇到了符号执行方法,想起来上学期上《形式化方法》课有专门关于符号执行的内容,在此先就课堂内容和课后作业对符号执行做一个简要的概述吧。
1 背景引言相关
1.1 程序验证方法的范围
程序安全性验证的技术如下:
横轴-Cost 程序验证的代价/要求(对程序员的要求、时间、经验等等)
纵轴-Confidence 可信度

(1)Ad-hoc Testing(随机测试)
随机测试是没有书面测试用例、记录期望结果、检查列表、脚本或指令的测试。主要是根据测试者的经验对软件进行功能和性能抽查。其需要花费的代价低,不过相应的其能提供的可信度也很低。
(2)Concolic Testing(混合测试)& Whitebox Fuzzing(白盒模糊测试)
混合测试是具体的符号执行测试,是具体执行和符号执行相结合,后面可能会单独写一篇文章进行介绍。【先立个flag在这hhhh】
模糊测试是一种通过向目标系统提供非预期的输入并监视异常结果来发现软件漏洞的方法,可分为黑盒模糊测试、白盒模糊测试和灰盒模糊测试,后面可能也有单独写文章介绍模糊测试。【第二个flag】
(3)Symbolic Execution(符号执行)
符号执行的代价高于前两种工具,但相应的可信度也提升了,可以实现全路径覆盖,也能发现一些其他工具发现不了的BUG。
工具举例:KLEE
(4)Extended Static Checking
(5)Static Analysis(静态分析/程序分析)
(6)Verification(验证)
1.2 使用符号执行的原因
1.2.1 黑盒测试的困难性
考虑下方代码什么时候会触发 “DivdieByZero” 异常?
int foo(int x, int y){
if(x==32467289)
return x/y;
else
return 0;
}
根据代码可知,当 x== 32467289 && y == 0 时,会触发 除零 异常。
当看不到源代码时,如何发现代码中的这一漏洞?
考虑黑盒模糊测试,即随机生成整型的输入值:
Foo(1, 1) √
Foo(1, 0) √
Foo(0, 0) √
……
直到 Foo(32467289, 0) 才会触发这个异常,所以采用模糊测试触发这个异常的概率为:1 / (2^64)
这一结果显示,黑盒测试发现异常非常艰难。
1.2.2 白盒测试的困难性
考虑下方代码,如果我们可以证明:无论怎么给 x、y 赋值,都不会触发 assert(x-y != 0),那么就可以对代码改写,将该句代码删除掉。
void foo(int a, int b){
int x = 1, y = 0;
if(a != 0){
y = 3+x;
if(b == 0)
x = 2*(a+b);
}
assert(x-y != 0);
}当采用下方测试用例进行测试时:
输入:a = 0, b =0;输出:x = 1, y = 0;
输入:a = 1, b = 0;输出:x = 2, y = 4;
输入:a = 1, b = 1;输出:x = 1, y = 4;
……
需要有较多测试用例,比较麻烦。
上述结果表明,在没有理论指导进行测试的情况下,白盒测试可能也很难发现代码中的错误。
1.2.3 自动生成测试用例
关键思想:对于给定的程序,是否有一个方法或者工具可以自动生成一组测试用例,要求效率要高,并且测试用例要满足一定的性质。
所以考虑 符号执行(Symbolic Execution)。
2 符号执行原理及理解
2.1 符号执行原理
符号执行是一种程序分析技术,它可以通过分析程序来得到让特定代码区域执行的输入。
当使用符号执行分析一个程序时,该程序会
使用符号值作为输入
,而非一般执行程序时使用的具体值。
在达到目标代码时,分析器可以得到相应的路径约束,然后通过约束求解器来得到可以触发目标代码的具体值。
2.2 符号执行理解
以下方代码为例:
int foo(int x, int y){
int z = x+y;
if(x==32467289)
return x/y;
else
return 0;
}
#1 构造符号值作为函数输入,符号值常用变量名称
此处为:
| 变量 | 值 |
| x | x |
| y | y |
#2 使用“符号输入”执行程序,保持符号程序状态
##2.1 对于普通语句,直接执行
执行完语句“int z = x + y”后,符号程序状态如下:
| 变量 | 值 |
| x | x |
| y | y |
| z | x + y |
##2.2 对于分支语句,向各个分支添加相应的“路径条件”
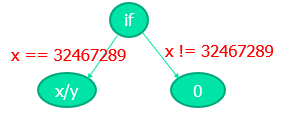
即:
if (x == 32467289)
路径条件:x == 32467289
return x/y;
else
路径条件:x != 32467289
return 0;
#3 根据路径条件和属性,我们可以生成约束
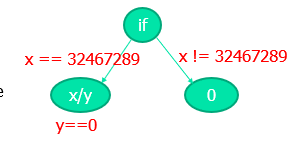
约束为可能触发异常的路径条件和属性。
如上图所示,右分支不可能触发异常;左分支在 y== 0 时会触发除零异常,所以约束为:
x == 32467289 /\ y == 0
即:
if (x == 32467289)
路径条件:x == 32467289
return x/y;
y == 0
else
路径条件:x != 32467289
return 0;
#4 将生成的约束馈送到某个求解器(例如Z3),以检查可满足性
The
model:
[x
=
32467289,
y==0]
#5 验证步骤
将求解器中的模型用作具体输入,看是否会触发异常。
2.3 符号执行架构
上述执行过程如下图所示:

symbolic executor:相当于Z3
path conditions:路径条件
solver:求解器,例如Z3
model:模型 如果是UNSAT,则表明程序中不存在bug;如果是SAT,则需要将其作为具体输入执行程序看是否会触发bug。
3 符号执行实例
符号执行下方程序:
void foo(int a, int b){
int x = 1, y = 0;
if(a != 0){
y = 3+x;
if(b == 0)
x = 2*(a+b);
}
assert(x-y != 0);
}
如果对于所有的 x、y,都不存在 x == y 的情况,则最后一句”assert( x – y != 0) 可以删除,那么我们需要判断的就是
x-y == 0
。
所以约束为:
路径条件 /\ x – y == 0
。
构造符号值:
| 变量 | 值 |
| a | a |
| b | b |
| x | 1 |
| y | 0 |
对于第一个分支:if( a != 0 )
(1)路径条件:a == 0
| 变量 | 值 |
| a | a |
| b | b |
| x | 1 |
| y | 0 |
约束为:a == 0 /\ 1 – 0 == 0,显然UNSAT。
(2)路径条件:a != 0
| 变量 | 值 | 语句 |
| a | a | / |
| b | b | / |
| x | 1 | / |
| y | 4 | y = x + 3 |
a. 路径条件:b ! = 0
| 变量 | 值 |
| a | a |
| b | b |
| x | 1 |
| y | 4 |
约束为:a != 0 /\ b != 0 /\ 1 – 4 == 0,显然也是UNSAT。
b. 路径条件:b == 0
| 变量 | 值 | 操作 |
| a | a | / |
| b | b | / |
| x | 2 * (a + b) | x = 2 * (a + b) |
| y | 4 | / |
约束为:a != 0 /\ b == 0 /\ 2 * (a + b) – 4 == 0
将约束馈入Z3,得到
model [ a = 2, b = 0 ]
。
将 [ a =2, b = 0 ] 代入源程序,发现确实 x – y == 0。