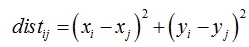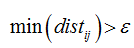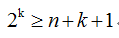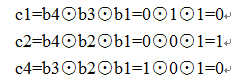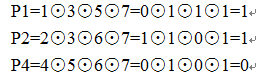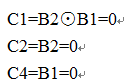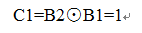最近学习AR,买了本Mastering OpenCV,这书上有两个AR的例子,这里先分析的是第二章基于标识的AR,书中是使用Xcode给iphone或者ipad写的,本文是在linux系统上vim实现的,终端模式。
先推荐两个前辈的博客,本文参考了二者和书进行理解源码。
http://blog.csdn.net/jinshengtao/article/details/48604435 taotao1233写的,大部分是基于他的博客,称转载也可以。
http://blog.csdn.net/acorld/article/details/8747813 missjuan写的,就是分析在xcode上进行实现的。
我的程序源码已经上传到
http://download.csdn.net/detail/chuhang_zhqr/9298975
,有需要的请下载。
以下开始进行分析:
程序大体框架:
1:对输入图像帧进行标记检测,这里包括,灰度化,找到图像中轮廓,搜索可能的标记;检测和解码标记,
2:估计标记的三维姿态,这里包括提前对摄像机进行相机标定,获取相机内参数和失真系数,根据这个计算出标记的旋转矩阵和平移矩阵。
3:由相机内参数和标记的旋转矩阵和平移矩阵,用OpenGL进行渲染三维物体;
以上是实现AR的必经之路,我认为OpenCV实现就已经很底层了,再底层那就太麻烦了,在科研的道路上,工程化实现未尝不可。
因为是刚把源码实现了,没来及完善工程,决定趁热打铁先记录一下心路历程。
现在开始分析源码,从第一步开始,输入图像:输入图像帧无非三种源,图片,视频,摄像头。和书上一样先使用图片吧。就是这个图片
书上的不是640×480的,我修了一下。
src = imread("1.jpg");
1):灰度化处理:
必须将输入图像转换为灰度图,因为标识仅包含黑白块,这使得更容易在灰度图像上操作这些块。
//彩色转换成灰色图像
cvtColor(src,grayscale,CV_BGRA2GRAY);
}
这个没什么好说的,
2):执行二值化阈值操作:
将图像的每个像素变成黑色或白色,为检测轮廓做准备,使用合理的自适应阈值法,减小光照条件和软强度变化影响。以需要二值化的像素为中心,将给定半径内的所有像素的平均强度作为该像素的强度,使轮廓检测更具有鲁棒性。
adaptiveThreshold(grayscale,//Input Image
thresholdImg,//Result binary image
255,
ADAPTIVE_THRESH_GAUSSIAN_C,
THRESH_BINARY_INV,
7,
7
);
/*输入图像
//输出图像
//使用 CV_THRESH_BINARY 和 CV_THRESH_BINARY_INV 的最大值
//自适应阈值算法使用:CV_ADAPTIVE_THRESH_MEAN_C 或 CV_ADAPTIVE_THRESH_GAUSSIAN_C
//取阈值类型:必须是下者之一
//CV_THRESH_BINARY,
//CV_THRESH_BINARY_INV
//用来计算阈值的象素邻域大小: 3, 5, 7, ...
*/
3):轮廓检测:
使用findContours检测输入图像的轮廓。
//检测所输入的二值图像的轮廓,返回一个多边形列表,其每个多边形标识一个轮廓,小轮廓不关注,不包括标记...
void MarkerDetector::findContour(cv::Mat& thresholdImg, ContoursVector& contours, int minContourPointsAllowed) const
{
ContoursVector allContours;
/*输入图像image必须为一个2值单通道图像
//检测的轮廓数组,每一个轮廓用一个point类型的vector表示
//轮廓的检索模式
CV_RETR_EXTERNAL表示只检测外轮廓
CV_RETR_LIST检测的轮廓不建立等级关系
CV_RETR_CCOMP建立两个等级的轮廓,上面的一层为外边界,里面的一层为内孔的边界信息。如果内孔内还有一个连通物体,这个物体的边界也在顶层。
CV_RETR_TREE建立一个等级树结构的轮廓。具体参考contours.c这个demo
//轮廓的近似办法
CV_CHAIN_APPROX_NONE存储所有的轮廓点,相邻的两个点的像素位置差不超过1,即max(abs(x1-x2),abs(y2-y1))==1
CV_CHAIN_APPROX_SIMPLE压缩水平方向,垂直方向,对角线方向的元素,只保留该方向的终点坐标,例如一个矩形轮廓只需4个点来保存轮廓信息
CV_CHAIN_APPROX_TC89_L1,CV_CHAIN_APPROX_TC89_KCOS使用teh-Chinl chain 近似算法
offset表示代表轮廓点的偏移量,可以设置为任意值。对ROI图像中找出的轮廓,并要在整个图像中进行分析时,这个参数还是很有用的。
*/
findContours(thresholdImg, allContours, CV_RETR_LIST, CV_CHAIN_APPROX_NONE);
contours.clear();
for(size_t i=0;i<allContours.size();i++)
{
int contourSize = allContours[i].size();
if(contourSize > minContourPointsAllowed)
{
contours.push_back(allContours[i]);
}
}
//Mat result(src.size(),CV_8U,Scalar(0));
//drawContours(result,detectedMarkers,-1,Scalar(255),2);
//imshow("AR based marker...",result);
}
其函数返回值为一个多边形列表,其每个多边形都表示一个轮廓。若轮廓包含的像素数比minContourPointsAllowed还小,则是一个小轮廓,这里不感兴趣,直接去除,这些小轮廓可能并没有包含标记。
4):搜索候选标记:
在找到轮廓后,将开始进行多边形逼近,这样做为了减少轮廓的像素。因为标记总是被四个顶点的多边形包含,如果不是四个,就不是我们想要的标记。筛选出非标记区域。
用Opencv内置API检测多边形,通过判断多边形定点数量是否为4,四边形各顶点之间相互距离是否满足要求(四边形是否足够大),过滤非候选区域。然后再根据候选区域之间距离进一步筛选,得到最终的候选区域,并使得候选区域的顶点坐标逆时针排列。
a. 四边形顶点之间距离
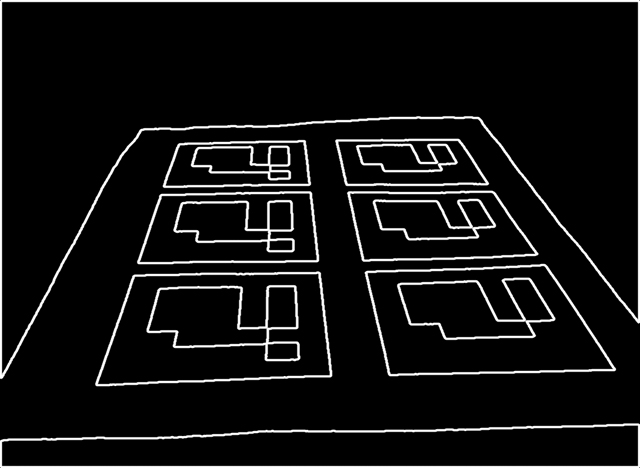
对每个四边形S,计算其相邻顶点之间的距离:
上式中i,j为相邻的两个顶点,若顶点之间的最小值仍大于阈值,则保留该四边形S进行下一步判断。
b. 四边形之间距离
求四边形S和S’之间的距离,即计算四个顶点之间的平均距离:
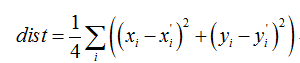
若dist小于阈值,则四边形S和S’距离较近,记录到tooNearCandidates向量里。接来下perimeter函数分别求四边形S和S’四个顶点之间的距离和,保留距离较大的,将距离较小的放入removalMask数组中,下式中i,j为四边形内相邻顶点
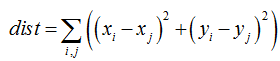
c. 行列式的几何意义—逆时针排序
行列式是由一些数据排列成的方阵经过规定的计算方法而得到的一个数。那它的几何意义是什么呢?有两种解释:
一个是行列式就是行列式中的行或列向量所构成的超平行多面体的有向面积或有向体积;
另一个是矩阵A的行列式detA就是线性变化A下的图形面积或体积的伸缩因子;
接下来的代码中,由于在approxPolyDP寻找多边形时,顶点摆放次序有逆时针和顺时针两种,我们希望这些顶点按照逆时针摆放。因此,对于四边形而言,我们只讨论2*2行列式对应的有向面积。
一个2×2矩阵A的行列式,是A的行向量(或列向量)决定的平行四边形的有向面积。用几何观点来看,二阶行列式D是XOY平面上以行向量a=(a1,a2),b=(b1,b2)为邻边的平行
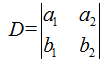
四边形的有向面积。若这个平行四边形是由向量a沿逆时针方向转到b而得到的,面积取正值;若这个平行四边形是由向量a沿顺时针方向转到而得到的,面积取负值。本例中,对于顺时针摆放的顶点0,1,2,3,咱可以通过计算有0-1,0-2构成的向量计算其有向面积。如果是顺时针摆放,那么该有向面积一定是负数,只要交换1,3位置即可。
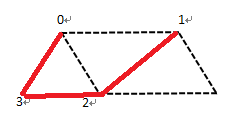
//由于我们的标记是四边形,当找到图像所有轮廓细节后,本文用Opencv内置API检测多边形,通过判断多边形定点数量是否为4,四边形各顶点之间相互距离是否满足要求(四边形是否足够大),过滤非候选区域。然后再根据候选区域之间距离进一步筛选,得到最终的候选区域,并使得候选区域的顶点坐标逆时针排列。
void MarkerDetector::findCandidates(const ContoursVector& contours,vector<Marker>& detectedMarkers)
{
vector<Point> approxCurve;//返回结果为多边形,用点集表示//相似形状
vector<Marker> possibleMarkers;//可能的标记
//For each contour,分析它是不是像标识,找到候选者//分析每个标记,如果是一个类似标记的平行六面体...
for(size_t i=0;i<contours.size();i++)
{
/*近似一个多边形逼近,为了减少轮廓的像素。这样比较好,可筛选出非标记区域,因为标记总能被四个顶点的多边形表示。如果多边形的顶点多于或少于四个,就绝对不是本项目想要的标记。通过点集近似多边形,第三个参数为epsilon代表近似程度,即原始轮廓及近似多边形之间的距离,第四个参数表示多边形是闭合的。*/
double eps = contours[i].size()*0.05;
//输入图像的2维点集,输出结果,估计精度,是否闭合。输出多边形的顶点组成的点集//使多边形边缘平滑,得到近似的多边形
approxPolyDP(contours[i],approxCurve,eps,true);
//我们感兴趣的多边形只有四个顶点
if(approxCurve.size() != 4)
continue;
//检查轮廓是否是凸边形
if(!isContourConvex(approxCurve))
continue;
//确保连续点之间的距离是足够大的。//确保相邻的两点间的距离“足够大”-大到是一条边而不是短线段就是了
//float minDist = numeric_limits<float>::max();//代表float可以表示的最大值,numeric_limits就是模板类,这里表示max(float);3.4e038
float minDist = 1e10;//这个值就很大了
//求当前四边形各顶点之间的最短距离
for(int i=0;i<4;i++)
{
Point side = approxCurve[i] - approxCurve[(i+1)%4];//这里应该是2维的相减
float squaredSideLength = side.dot(side);//求2维向量的点积,就是XxY
minDist = min(minDist,squaredSideLength);//找出最小的距离
}
//检查距离是不是特别小,小的话就退出本次循环,开始下一次循环
if(minDist<m_minContourLengthAllowed)
continue;
//所有的测试通过了,保存标识候选,当四边形大小合适,则将该四边形maker放入possibleMarkers容器内 //保存相似的标记
Marker m;
for(int i=0;i<4;i++)
m.points.push_back(Point2f(approxCurve[i].x,approxCurve[i].y));//vector头文件里面就有这个push_back函数,在vector类中作用为在vector尾部加入一个数据。
/*逆时针保存这些点
//从代码推测,marker中的点集本来就两种序列:顺时针和逆时针,这里要把顺时针的序列改成逆时针,在多边形逼近时,多边形是闭合的,则不是顺时针就是逆时针
//在第一个和第二个点之间跟踪出一条线,如果第三个点在右边,则点是逆时针保存的//逆时针排列这些点,第一个点和第二个点之间连一条线,如果第三个点在边,那么这些点就是逆时针*/
Point v1 = m.points[1] - m.points[0];
Point v2 = m.points[2] - m.points[0];
/*行列式的几何意义是什么呢?有两个解释:一个解释是行列式就是行列式中的行或列向量所构成的超平行多面体的有向面积或有向体积;另一个解释是矩阵A的行列式detA就是线性变换A下的图形面积或体积的伸缩因子。
//以行向量a=(a1,a2),b=(b1,b2)为邻边的平行四边形的有向面积:若这个平行四边形是由向量沿逆时针方向转到b而得到的,面积取正值;若这个平行四边形是由向量a沿顺时针方向转到而得到的,面积取负值; */
double o = (v1.x * v2.y) - (v1.y * v2.x);
if(o<0.0) //如果第三个点在左边,那么交换第一个点和第三个点,逆时针保存
swap(m.points[1],m.points[3]);
possibleMarkers.push_back(m);//把这个标识放入候选标识向量中
}
//移除那些角点互相离的太近的四边形//移除角点太接近的元素
vector< pair<int,int> > tooNearCandidates;
for(size_t i=0;i<possibleMarkers.size();i++)
{
const Marker& m1 = possibleMarkers[i];
//计算两个maker四边形之间的距离,四组点之间距离和的平均值,若平均值较小,则认为两个maker很相近,把这一对四边形放入移除队列。//计算每个边角到其他可能标记的最近边角的平均距离
for(size_t j=i+1;j<possibleMarkers.size();j++)
{
const Marker& m2 = possibleMarkers[j];
float distSquared = 0;
for(int c=0;c<4;c++)
{
Point v = m1.points[c] - m2.points[c];
//向量的点乘-》两点的距离
distSquared += v.dot(v);
}
distSquared /= 4;
if(distSquared < 100)
{
tooNearCandidates.push_back(pair<int,int>(i,j));
}
}
}
//移除了相邻的元素对的标识
//计算距离相近的两个marker内部,四个点的距离和,将距离和较小的,在removlaMask内做标记,即不作为最终的detectedMarkers
vector<bool> removalMask(possibleMarkers.size(),false);//创建Vector对象,并设置容量。第一个参数是容量,第二个是元素。
for(size_t i=0;i<tooNearCandidates.size();i++)
{
//求这一对相邻四边形的周长
float p1 = perimeter(possibleMarkers[tooNearCandidates[i].first].points);
float p2 = perimeter(possibleMarkers[tooNearCandidates[i].second].points);
//谁周长小,移除谁
size_t removalIndex;
if(p1 > p2)
removalIndex = tooNearCandidates[i].second;
else
removalIndex = tooNearCandidates[i].first;
removalMask[removalIndex] = true;
}
//返回候选,移除相邻四边形中周长较小的那个,放入待检测的四边形的队列中。//返回可能的对象
detectedMarkers.clear();
for(size_t i = 0;i<possibleMarkers.size();i++)
{
if(!removalMask[i])
detectedMarkers.push_back(possibleMarkers[i]);
}
}在这里有个周长的函数:
float perimeter(const vector<Point2f> &a)//求多边形周长。
{
float sum=0,dx,dy;
for(size_t i=0;i<a.size();i++)
{
size_t i2=(i+1) % a.size();
dx = a[i].x - a[i2].x;
dy = a[i].y - a[i2].y;
sum += sqrt(dx*dx + dy*dy);
}
return sum;
}现在我们得到了一系列四边形,并且四个点按逆时针排序,它们可能是标记。下面开始验证是否为标记。
5:首先为获得四边形区域的正面视图,应该删除透视投影。
为了得到四边形变换后的矩形标记图像,必须通过透视变换来变换图像,变换矩阵通过getPerspectiveTransform计算得到。该函数通过四边形顶点来得到透视变换矩阵。函数的第一个参数为标记在图像空间的坐标;第二个参数为方形标记图像四个顶点的坐标。
void MarkerDetector::recognizeMarkers(const Mat& grayscale,vector<Marker>& detectedMarkers)
{
Mat canonicalMarkerImage;
char name[20] = "";
vector<Marker> goodMarkers;
/*Identify the markers识别标识 //分析每一个捕获到的标记,去掉透视投影,得到平面/正面的矩形。
//为了得到这些矩形的标记图像,我们不得不使用透视变换去恢复(unwarp)输入的图像。这个矩阵应该使用cv::getPerspectiveTransform函数,它首先根据四个对应的点找到透视变换,第一个参数是标记的坐标,第二个是正方形标记图像的坐标。估算的变换将会把标记转换成方形,从而方便我们分析。 */
for(size_t i=0;i<detectedMarkers.size();i++)
{
Marker& marker = detectedMarkers[i];
//找到透视转换矩阵,获得矩形区域的正面视图// 找到透视投影,并把标记转换成矩形,输入图像四边形顶点坐标,输出图像的相应的四边形顶点坐标
// Find the perspective transformation that brings current marker to rectangular form
Mat markerTransform = getPerspectiveTransform(marker.points,m_markerCorners2d);//输入原始图像和变换之后的图像的对应4个点,便可以得到变换矩阵
/* Transform image to get a canonical marker image
// Transform image to get a canonical marker image
//输入的图像
//输出的图像
//3x3变换矩阵 */
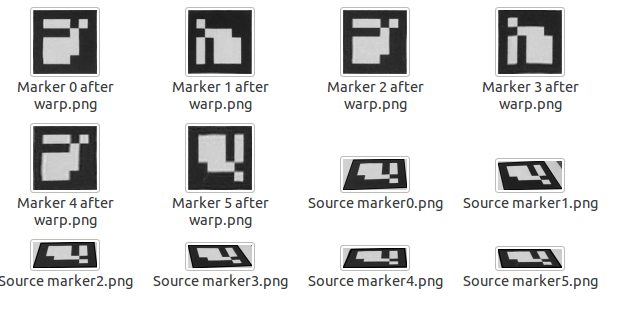
warpPerspective(grayscale,canonicalMarkerImage,markerTransform,markerSize);//对图像进行透视变换,这就得到和标识图像一致正面的图像,方向可能不同,看四个点如何排列的了。感觉这个变换后,就得到只有标识图的正面图
// sprintf(name,"warp_%d.jpg",i);
// imwrite(name,canonicalMarkerImage);
#ifdef SHOW_DEBUG_IMAGES
{
Mat markerImage = grayscale.clone();
marker.drawContour(markerImage);
Mat markerSubImage = markerImage(boundingRect(marker.points));
imshow("Source marker" + ToString(i),markerSubImage);
imwrite("Source marker" + ToString(i) + ".png",markerSubImage);
imshow("Marker " + ToString(i),canonicalMarkerImage);
imwrite("Marker " + ToString(i) + ".png",canonicalMarkerImage);
}
#endif
然后检查所得的方形图像是否为一个有效的标记图像。为了让标记只包含黑白两种颜色,对候选标记区域的灰度图使用大律OSTU算法,求取二值化图,去除灰色像素,只留下黑白像素。(之前不用OSTU是大范围图片,会影响性能)。Otsu算法假定图像直方图呈双峰分布,然后搜索一个阈值,该阈值使得类间(extra-calss)的方差尽可能大,而使类内(inter-class)的方差尽可能小。
int Marker::getMarkerId(Mat& markerImage,int &nRotations)
{
assert(markerImage.rows == markerImage.cols);//如果它的条件返回错误,则终止程序执行
assert(markerImage.type() == CV_8UC1);
Mat grey = markerImage;
//Threshold image使用Otsu算法移除灰色的像素,只留下黑色和白色像素。
//这是固定阀值方法
//输入图像image必须为一个2值单通道图像
//检测的轮廓数组,每一个轮廓用一个point类型的vector表示
//阀值
//max_value 使用 CV_THRESH_BINARY 和 CV_THRESH_BINARY_INV 的最大值
//type
threshold(grey,grey,125,255,THRESH_BINARY | THRESH_OTSU);//对候选标记区域的灰度图使用大律OSTU算法,求取二值化图,大范围图片用这个算法会影响性能。
#ifdef SHOW_DEBUG_IMAGES
imshow("Binary marker",grey);
imwrite("Binary marker" + ".png",grey);
#endif
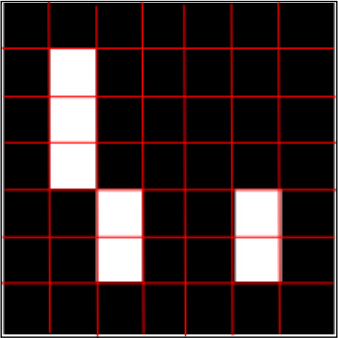
最后进行标记编码识别。每个标记都有一个内部编码。标记被分成7×7的网格,其中内部5×5的网格包含ID信息。其余部分是黑色边界。因此首先需要检查外部黑色边界是否存在,然后读取5×5的网格是否存在有效的标记编码(因为检测出来的标记可能是旋转的,要旋转标记编码来得到有效的标记编码)。
每个标记可以划分成7*7个方格,黑格子表示0,白格子表示1。这样标记内部将有5个数字,而每个数字由5个bit表示。具体编码方式类似于海明码,3个bit用于校验,2个bit用于存放数据,因此每5个bit可以表达4种数据,而5行这样的编码可以表达4^5=1024个数据。如下图所示:
接下来,咱有必要复习下《计算机组成原理》的海明码,在唐硕飞老师课本的P100页存储器的校验一节有提到。注意:海明码只有一位纠错能力!!
在计算机运行过程中,由于种种原因致使数据在存储过程中可能出现差错。为了能及时发现错误并纠正错误,通常可将原数据配成海明编码。设欲检测的二进制代码为n位,为使其具有纠错能力,需增添k位检测位,组成n+k位的代码。为了能准确对错误定位以及指出代码没错,新增添的检测位数k应满足:
稍稍解释一下,不等式左边代表该类编码允许的出错数量共2k种;不等式右边,若数据位中有一位出错,那就有n种可能,若校验位自身有一位错误,那就有k种可能,若完全没错,那也是一种可能,因此n+k+1。
设n+k位代码自左至右依次编码为第1,2,3,…,n+k位,而将第k位检测位记作Ci,分别安插在n+k位代码编号的第1,2,4,8,…,2k-1位上。这些检测位的位置设置是为了保证它们能分别承担n+k位信息中不同数据位所组成的“小组“的奇偶检测任务,使检测位和它所负责检测的小组中1的个数为奇数或偶数。以下是根据检测特性P101规定死的:
C1 检测的g1小组包含1,3,5,7,9,11,…位
C2 检测的g2小组包含2,3,6,7,10,11,14,15…位
C4 检测的g3小组包含4,5,6,7,12,13,14,15…位
海明校验就是在编码后,通过故障字的值确定码子中哪一位发生了错误,并将其取反纠正错误。
例1:想传递数据位0101,则要配备3位校验位c1c2b4c4b3b2b1,按照配偶原则:
故最终的海明码即为0100101
例2:已知接收到的海明码为0110101按照配偶原则,试问想要传送的信息是啥?
接收到的7位编码,包含了3位校验码分别在第1,2,4位,首先判断收到的信息是否出错,纠错过程如下:
所以,P4P2P1=011,第3位出错,可纠正为0100101,故欲传递的信息为0101.
本书中采用3位校验码2位数据码,则1,2,4位是校验位,3,5是数据位。同时为了防止将全黑色的四边形识别成合法的marker,增强算法鲁棒性,修改了3,5位数据校验的奇偶性。即对于传递数据为00的情形C1C2B2C4B1,要避免00000,本来是这样的:
现在是这样的,10000
在温故海明码后,我们可以识别候选四边形区域内的数据信息,确定该四边形是否为最初定义的Marker。
程序分析:
//在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的字符不同的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
int Marker::hammDistMarker(Mat bits)//对每个可能的标记方向找到海明距离,和参考标识一致的为0,其他旋转形式的标记不为0,因为经过透射变换后,只能得到四个方向的标记,则旋转四次,找到和参考标识一致的方向。
{
int ids[4][5]=
{
{1,0,0,0,0},
{1,0,1,1,1},
{0,1,0,0,1},
{0,1,1,1,0}
};
int dist = 0;
for(int y=0;y<5;y++)
{
int minSum = 1e5;//每个元素的海明距离
for(int p=0;p<4;p++)
{
int sum=0;
//now,count
for(int x=0;x<5;x++)
{
sum += bits.at<uchar>(y,x) == ids[p][x]?0:1;
}
if(minSum>sum)
minSum=sum;
}
dist += minSum;
}
return dist;
}
int Marker::mat2id(const Mat& bits)//移位,求或,再移位,得到最终的ID
{
int val=0;
for(int y=0;y<5;y++)
{
val<<=1;//移位操作
if(bits.at<uchar>(y,1)) val |= 1;
val<<=1;
if(bits.at<uchar>(y,3)) val |= 1;
}
return val;
}
首先检查四边形轮廓是否完整,即通过统计方块内非零像素值个数,若大于方块内像素个数的一半,则认为该方块是白色的。按行遍历所有轮廓方格,方格大小为100/7,只要有一个轮廓方格被判定为白色,那么整个轮廓就是不完整的,舍弃该Marker
然后,同理识别5*5编码区域,将0-1编码写入bitMatrix矩阵。由于IPAD拍摄照片存在旋转变化,因此每个矩形方格具有四种旋转状态,即直接从当前矩形区域解码可能是旋转过的图片,不能代表真正的数据。
本文为所有旋转状态下的Marker计算海明距离,选择海明距离最小的作为最终的编码矩阵。海明距离的计算:
hammDistMarker函数中,ids数组的由来。咱采用3位校验2位数据,因此每个stripe的2位数据将产生4种海明编码。也就是说ids数组列举了Marker中每行数据的所有可能取值。
Marker中的一行表示一个数据,我们把bitMatrix的每一行同ids中的一行数据依次比较,总能寻找到ids中最贴近bitMatrix第x行的一行ids。再把bitMatrix对应的ids值求和,即可得到海明距离。
最后,在确定了Marker的旋转状态后,mat2id函数对该Marker进行解码,即遍历各行,或运算、移位运算得到最终的ID。
//所使用的标记都有一个内部的5x5编码,采用的是简单修改的汉明码。简单的说,就是5bits中只有2bits被使用,其他三位都是错误的识别码,也就是说我们至多有1024种不同的标识。我们的汉明码最大的不同是,汉明码的第一位(奇偶校验位的3和5)是反向的。所有ID 0(在汉明码是00000),在这里是10000,目的是减少环境造成的影响.
//标识被划分为7x7的网格,内部的5x5表示标识内容,额外的是黑色边界,接下来是逐个检查四条边的像素是否都是黑色的,若有不是黑色,那么就不是标识。
int cellSize = markerImage.rows/7;
for(int y=0;y<7;y++)
{
int inc = 6;
if(y == 0 || y == 6) inc=1;//对第一行和最后一行,检查整个边界
for(int x=0;x<7;x+=inc)
{
int cellX = x*cellSize;
int cellY = y*cellSize;
Mat cell = grey(Rect(cellX,cellY,cellSize,cellSize));
int nZ = countNonZero(cell);//统计区域内非0的个数。
if(nZ > (cellSize*cellSize)/2)
{
return -1;//如果边界信息不是黑色的,就不是一个标识。
}
}
}
Mat bitMatrix = Mat::zeros(5,5,CV_8UC1);
//得到信息(对于内部的网格,决定是否是黑色或白色的)就是判断内部5x5的网格都是什么颜色的,得到一个包含信息的矩阵bitMatrix。
for(int y=0;y<5;y++)
{
for(int x=0;x<5;x++)
{
int cellX = (x+1)*cellSize;
int cellY = (y+1)*cellSize;
Mat cell = grey(Rect(cellX,cellY,cellSize,cellSize));
int nZ = countNonZero(cell);
if(nZ > (cellSize*cellSize)/2)
bitMatrix.at<uchar>(y,x) = 1;
}
}
//检查所有的旋转
Mat rotations[4];
int distances[4];
rotations[0] = bitMatrix;
distances[0] = hammDistMarker(rotations[0]);//求没有旋转的矩阵的海明距离。
pair<int,int> minDist(distances[0],0);//把求得的海明距离和旋转角度作为最小初始值对,每个pair都有两个属性值first和second
for(int i=1;i<4;i++)//就是判断这个矩阵与参考矩阵旋转多少度。
{
//计算最近的可能元素的海明距离
rotations[i] = rotate(rotations[i-1]);//每次旋转90度
distances[i] = hammDistMarker(rotations[i]);
if(distances[i] < minDist.first)
{
minDist.first = distances[i];
minDist.second = i;//这个pair的第二个值是代表旋转几次,每次90度。
}
}
nRotations = minDist.second;//这个是将返回的旋转角度值
if(minDist.first == 0)//若海明距离为0,则根据这个旋转后的矩阵计算标识ID
{
return mat2id(rotations[minDist.second]);
}
return -1;
}确定了Marker的旋转状态后,对四边形顶点按照旋转状态排序,无论相机如何拍摄都使四边形中间的顶点排在第一个。 而后,通过亚像素技术cornerSubPix函数对顶点位置进一步细。所谓亚像素,两个像素之间,还存在像素,它完全由计算得到。
int nRotations;
int id = Marker::getMarkerId(canonicalMarkerImage,nRotations);
cout << "ID: " << id << endl;
if(id!=-1)
{
marker.id = id;
//sort the points so that they are always in the same order no matter the camera orientation
//Rotates the order of the elements in the range [first,last), in such a way that the element pointed by middle becomes the new first element.
//根据相机的旋转,调整标记的姿态
rotate(marker.points.begin(),marker.points.begin() + 4 - nRotations,marker.points.end());//就是一个循环移位
goodMarkers.push_back(marker);
}
}
//refine using subpixel accuracy the corners 是把所有标识的四个顶点都放在一个大的向量中。
if(goodMarkers.size() > 0)
{
//找到所有标记的角点
vector<Point2f> preciseCorners(4*goodMarkers.size());//每个marker四个点
for(size_t i=0;i<goodMarkers.size();i++)
{
Marker& marker = goodMarkers[i];
for(int c=0;c<4;c++)
{
preciseCorners[i*4+c] = marker.points[c];//i表示第几个marker,c表示某个marker的第几个点
}
}
//Refines the corner locations.The function iterates to find the sub-pixel accurate location of corners or radial saddle points
//类型
/*
CV_TERMCRIT_ITER 用最大迭代次数作为终止条件
CV_TERMCRIT_EPS 用精度作为迭代条件
CV_TERMCRIT_ITER+CV_TERMCRIT_EPS 用最大迭代次数或者精度作为迭代条件,决定于哪个条件先满足
//迭代的最大次数
//特定的阀值 */
TermCriteria termCriteria = TermCriteria(TermCriteria::MAX_ITER | TermCriteria::EPS,30,0.01);//这个是迭代终止条件,这里是达到30次迭代或者达到0.01精度终止。角点精准化迭代过程的终止条件
/*输入图像
//输入的角点,也作为输出更精确的角点
//接近的大小(Neighborhood size)
//Aperture parameter for the Sobel() operator
//像素迭代(扩张)的方法 */
cornerSubPix(grayscale,preciseCorners,cvSize(5,5),cvSize(-1,-1),termCriteria);//发现亚像素精度的角点位置,第二个参数代表输入的角点的初始位置并输出精准化的坐标。在标记检测的早期的阶段没有使用cornerSubPix函数是因为它的复杂性-调用这个函数处理大量顶点时会耗费大量的处理时间,因此我们只在处理有效标记时使用。
//copy back,再把精准化的坐标传给每一个标识。// 保存最新的顶点
for(size_t i=0;i<goodMarkers.size();i++)
{
Marker& marker = goodMarkers[i];
for(int c=0;c<4;c++)
{
marker.points[c] = preciseCorners[i*4+c];
//cout<<"X:"<<marker.points[c].x<<"Y:"<<marker.points[c].y<<endl;
}
}
}
//画出细化后的矩形图片
Mat markerCornersMat(grayscale.size(),grayscale.type());
markerCornersMat = Scalar(0);
for(size_t i=0;i<goodMarkers.size();i++)
{
goodMarkers[i].drawContour(markerCornersMat,Scalar(255));
}
//imshow("Markers refined edges",grayscale*0.5 + markerCornersMat);
//imwrite("Markers refined edges" + ".png",grayscale*0.5 + markerCornersMat);
imwrite("refine.jpg",grayscale*0.5 + markerCornersMat);
detectedMarkers = goodMarkers;
}
在检测到标记并对标记ID解码后,需要细化它的角点,此操作最下一步在三维空间估计标记位置很有用。

下一节将分析标记姿态估计。