结构光标定
原理
原理综述
结构光标定主要是获得光平面的方程,利用光平面方程和特征点投影直线可计算特征点的空间三维坐标,其仿真模型如图所示:

激光器向标定板发射线激光,标定板两侧的端点通过相机光心最终在相机感光面上成像。通过两个端点的像素坐标,利用相机的内外参数可将像素坐标转换为相机坐标系下的坐标,以相机光心为相机坐标系的原点坐标,利用这三个点的坐标可计算投影平面的方程。以标定板左上角为原点建立标定板坐标系,利用标定板坐标系转到相机坐标系的旋转矩阵和平移矩阵进行转换。将相机坐标系下标定板平面方程与投影平面方程联立可计算出相机坐标系下激光器射在标定板上的激光光条方程,取激光光条上任意一点,该点通过相机光心最终在相机感光面上成像,可获得其像素坐标,通过坐标系转换可获得相机坐标系下的坐标,结合相机光心可获得标定板投影直线的方向向量。将投影直线与激光光条进行联立可得到该点在相机坐标系下的空间坐标,即为光平面上的一点坐标。将标定板放置于不同位置并改变标定板的姿态,利用上述方法分别获得光平面上三个点坐标,通过三点计算平面方程算法可获得光平面的方程。
算法
已知以相机光心为相机坐标系原点
O
c
(
0
,
0
,
0
)
O_c(0,0,0)
O
c
(
0
,
0
,
0
)
,激光线射在标定板上得到两端点的投影三维坐标为
P
1
(
x
1
,
y
1
,
z
1
)
P_1(x_1,y_1,z_1)
P
1
(
x
1
,
y
1
,
z
1
)
,
P
2
(
x
2
,
y
2
,
z
2
)
P_2(x_2,y_2,z_2)
P
2
(
x
2
,
y
2
,
z
2
)
。利用三点可计算出两个方向向量,分别为:
O
c
P
1
⃗
\vec{O_cP_1}
O
c
P
1
和
O
c
P
2
⃗
\vec{O_cP_2}
O
c
P
2
。为得到面
O
c
P
1
P
2
O_cP_1P_2
O
c
P
1
P
2
的方程,需将两方向向量做叉乘运算得到平面的法向量
n
⃗
\vec{n}
n
:
n
1
⃗
=
O
c
P
1
⃗
×
O
c
P
2
⃗
=
∣
i
j
k
x
1
y
1
z
1
x
2
y
2
z
2
∣
=
(
a
1
,
b
1
,
c
1
)
\vec{n_1}=\vec{O_cP_1}\times\vec{O_cP_2}=\left| \begin{array}{cccc} i & j & k \\ x_1 & y_1 & z_1\\ x_2 & y_2 & z_2 \end{array} \right|=(a_1,b_1,c_1)
n
1
=
O
c
P
1
×
O
c
P
2
=
∣
∣
∣
∣
∣
∣
i
x
1
x
2
j
y
1
y
2
k
z
1
z
2
∣
∣
∣
∣
∣
∣
=
(
a
1
,
b
1
,
c
1
)
将上式展开为:
a
1
=
y
2
z
2
−
z
1
y
2
b
1
=
x
2
z
1
−
x
1
z
2
c
1
=
x
1
y
2
−
x
2
y
1
a_1=y_2z_2-z_1y_2\\ b_1=x_2z_1-x_1z_2\\ c_1=x_1y_2-x_2y_1
a
1
=
y
2
z
2
−
z
1
y
2
b
1
=
x
2
z
1
−
x
1
z
2
c
1
=
x
1
y
2
−
x
2
y
1
根据丘维声所著《解析几何(第三版)》第48-51页可知:该平面法向量所对应的元素
a
1
a_1
a
1
,
b
1
b_1
b
1
,
c
1
c_1
c
1
分别为平面方程一般式所对应的
a
1
a_1
a
1
,
b
1
b_1
b
1
,
c
1
c_1
c
1
。平面方程的
d
1
d_1
d
1
为:
d
1
=
−
(
a
1
x
1
+
b
1
y
1
+
c
z
1
)
d_1=-(a_1x_1+b_1y_1+cz_1)
d
1
=
−
(
a
1
x
1
+
b
1
y
1
+
c
z
1
)
至此,投影平面方程计算完毕,方程为:
a
1
x
+
b
1
y
+
c
1
z
+
d
1
=
0
a_1x+b_1y+c_1z+d_1=0
a
1
x
+
b
1
y
+
c
1
z
+
d
1
=
0
。
利用标定板上三点可计算出标定板平面方程的一般式为:
a
2
x
+
b
2
y
+
c
2
z
+
d
2
=
0
a_2x+b_2y+c_2z+d_2=0
a
2
x
+
b
2
y
+
c
2
z
+
d
2
=
0
。
通过两个平面的方程,对两平面的法向量进行叉乘运算可得到两平面交线的方向向量:
KaTeX parse error: Can’t use function ‘$’ in math mode at position 3: {$̲a_1x+b_1y+c_1z+…
两平面交线的方向向量
s
1
⃗
(
m
1
,
n
1
,
p
1
)
\vec{s_1}(m_1,n_1,p_1)
s
1
(
m
1
,
n
1
,
p
1
)
可表示为:
m
1
=
b
1
c
2
−
b
2
c
1
n
1
=
c
1
a
2
−
a
1
c
2
p
1
=
a
1
b
2
−
a
2
b
1
m_1=b_1c_2-b_2c_1\\ n_1=c_1a_2-a_1c_2\\ p_1=a_1b_2-a_2b_1
m
1
=
b
1
c
2
−
b
2
c
1
n
1
=
c
1
a
2
−
a
1
c
2
p
1
=
a
1
b
2
−
a
2
b
1
将像素坐标系下投影点坐标转换为相机坐标系下的坐标,利用该坐标
P
3
(
x
3
,
y
3
,
z
3
)
P_3(x_3,y_3,z_3)
P
3
(
x
3
,
y
3
,
z
3
)
和相机光心坐标计算出投影直线的方向向量
s
2
(
m
2
,
n
2
,
p
2
)
s_2(m_2,n_2,p_2)
s
2
(
m
2
,
n
2
,
p
2
)
。将激光光条方程与投影直线方程分别整理为“点向式”方程:
l
1
:
x
−
x
1
m
1
=
y
−
y
1
n
1
=
z
−
z
1
p
1
l
2
:
x
m
2
=
y
n
2
=
z
p
2
l_1:\frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1}\\ l_2:\frac{x}{m_2}=\frac{y}{n_2}=\frac{z}{p_2}
l
1
:
m
1
x
−
x
1
=
n
1
y
−
y
1
=
p
1
z
−
z
1
l
2
:
m
2
x
=
n
2
y
=
p
2
z
利用中间参数
t
t
t
可将直线上某点坐标表示为:
x
=
x
1
+
m
1
t
y
=
y
1
+
n
1
t
z
=
z
1
+
p
1
t
x=x_1+m_1t\\ y=y_1+n_1t\\ z=z_1+p_1t
x
=
x
1
+
m
1
t
y
=
y
1
+
n
1
t
z
=
z
1
+
p
1
t
将上式代入
l
2
l_2
l
2
中,得到
t
t
t
的值为:
t
=
m
2
y
1
−
n
2
x
1
m
1
n
2
−
m
2
n
1
t=\frac{m_2y_1-n_2x_1}{m_1n_2-m_2n_1}
t
=
m
1
n
2
−
m
2
n
1
m
2
y
1
−
n
2
x
1
将
t
t
t
代入
l
1
l_1
l
1
可得到空间两直线的交点
M
(
x
,
y
,
z
)
M(x,y,z)
M
(
x
,
y
,
z
)
。
移动标定板至不同距离,改变标定板姿态,利用上述算法获得光平面内一点,在得到三个点之后可计算出光平面的方程:
a
x
+
b
y
+
c
z
+
d
=
0
ax+by+cz+d=0
a
x
+
b
y
+
c
z
+
d
=
0
。
以上为结构光标定的全部算法。
调用步骤
步骤1:通过激光光条两端点坐标和光心坐标,利用calPlaneFrom3Points函数计算投影面方程,获得投影面方程参数
(
a
1
,
b
1
,
c
1
,
d
1
)
(a_1,b_1,c_1,d_1)
(
a
1
,
b
1
,
c
1
,
d
1
)
;
步骤2:通过标定板上三点坐标,利用calPlaneFrom3Points函数计算标定板平面方程,获得标定板平面方程参数
(
a
2
,
b
2
,
c
2
,
d
2
)
(a_2,b_2,c_2,d_2)
(
a
2
,
b
2
,
c
2
,
d
2
)
;
步骤3:通过投影平面方程和标定板平面方程,利用calVectorFrom2Planes函数计算两平面交线,即激光光条的方向向量
s
1
⃗
(
x
1
,
y
1
,
z
1
)
\vec{s_1}(x_1,y_1,z_1)
s
1
(
x
1
,
y
1
,
z
1
)
;
步骤4:利用calVectorFrom2Points函数计算激光光条某点的投影直线方向向量
s
2
(
x
2
,
y
2
,
z
2
)
s_2(x_2,y_2,z_2)
s
2
(
x
2
,
y
2
,
z
2
)
;
步骤5:通过激光光条端点、相机光心、激光光条方向向量和投影直线方向向量,利用calCoordinateFrom2Lines函数计算空间两直线交点;
步骤6:利用上述步骤获得光平面上另外两个点;
步骤7:通过光平面上的三个点,利用calPlaneFrom3Points函数计算光平面方程。
仿真结果
-
激光光条与投影直线交点,即光平面上某点仿真:
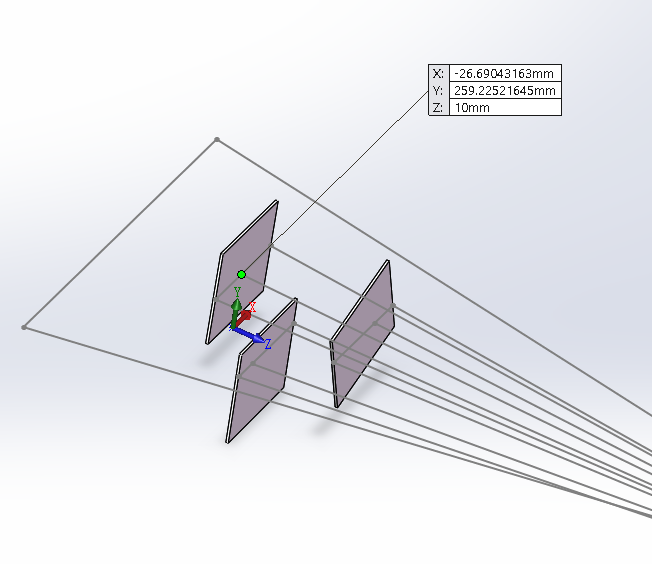
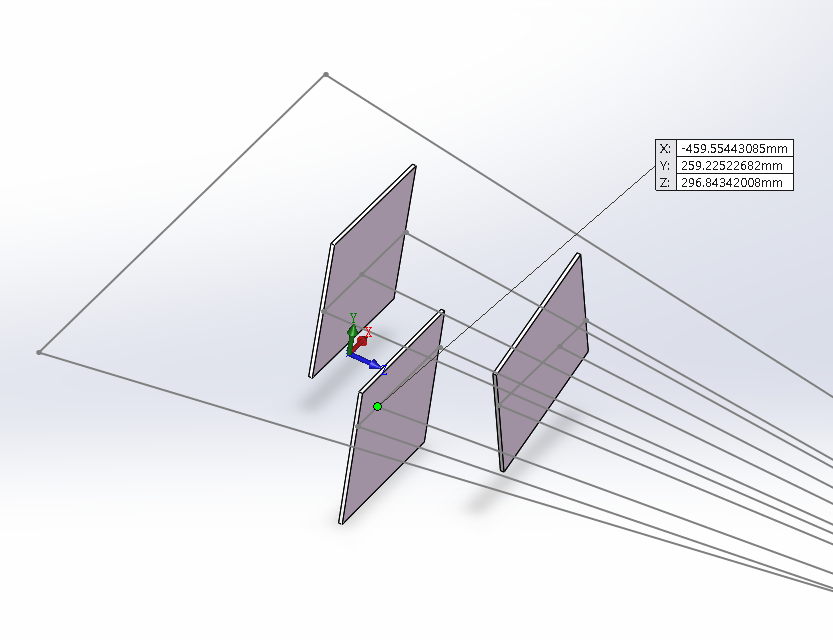
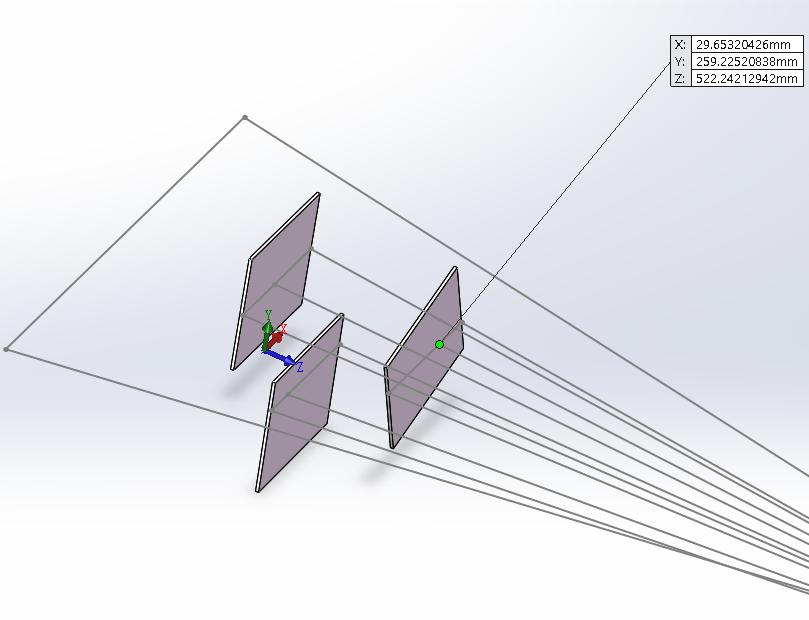
利用上述算法计算得到这三点的坐标为:
(
−
26.69043169
,
259.22521645
,
10
)
(-26.69043169,259.22521645,10)
(
−
2
6
.
6
9
0
4
3
1
6
9
,
2
5
9
.
2
2
5
2
1
6
4
5
,
1
0
)
(
−
459.55443126
,
259.22522682
,
296.84342008
)
(-459.55443126,259.22522682,296.84342008)
(
−
4
5
9
.
5
5
4
4
3
1
2
6
,
2
5
9
.
2
2
5
2
2
6
8
2
,
2
9
6
.
8
4
3
4
2
0
0
8
)
(
29.65320412
,
259.22520838
,
522.24212942
)
(29.65320412,259.22520838,522.24212942)
(
2
9
.
6
5
3
2
0
4
1
2
,
2
5
9
.
2
2
5
2
0
8
3
8
,
5
2
2
.
2
4
2
1
2
9
4
2
)
。
-
利用仿真图中光平面三个端点计算光平面方程参数为:
[0.00000000
e
+
00
,
4.63585112
e
+
06
,
−
0.00000000
e
+
00
,
−
1.20172951
e
+
09
]
[ 0.00000000e+00, 4.63585112e+06, -0.00000000e+00, -1.20172951e+09]
[
0
.
0
0
0
0
0
0
0
0
e
+
0
0
,
4
.
6
3
5
8
5
1
1
2
e
+
0
6
,
−
0
.
0
0
0
0
0
0
0
0
e
+
0
0
,
−
1
.
2
0
1
7
2
9
5
1
e
+
0
9
]
利用上述光平面标定算法计算光平面方程的参数为:
[7.62677727
e
−
03
,
2.37892978
e
+
05
,
2.90892896
e
−
03
,
−
6.16678586
e
+
07
]
[ 7.62677727e-03, 2.37892978e+05, 2.90892896e-03, -6.16678586e+07]
[
7
.
6
2
6
7
7
7
2
7
e
−
0
3
,
2
.
3
7
8
9
2
9
7
8
e
+
0
5
,
2
.
9
0
8
9
2
8
9
6
e
−
0
3
,
−
6
.
1
6
6
7
8
5
8
6
e
+
0
7
]
述光平面标定算法计算光平面方程的参数为:
[
7.62677727
e
−
03
,
2.37892978
e
+
05
,
2.90892896
e
−
03
,
−
6.16678586
e
+
07
]
[ 7.62677727e-03, 2.37892978e+05, 2.90892896e-03, -6.16678586e+07]
[
7
.
6
2
6
7
7
7
2
7
e
−
0
3
,
2
.
3
7
8
9
2
9
7
8
e
+
0
5
,
2
.
9
0
8
9
2
8
9
6
e
−
0
3
,
−
6
.
1
6
6
7
8
5
8
6
e
+
0
7
]