博客

问题背景

汉诺塔问题，是心理学实验研究常用的任务之一。该问题的主要材料包括三根高度相同的柱子和一些大小及颜色不同的圆盘，三根柱子分别为起始柱A、辅助柱B及目标柱C。

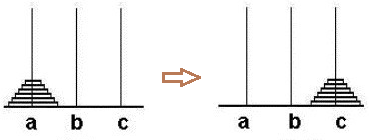
问题求解思路

解决方法：递归

使用的语言：C语言

编译环境：VS2022

解决思路：假设A柱中有n个圆盘，先借助C将n-1个圆盘从A移动到B中，将A中剩余的一个圆盘移动至C，再将B中n-1个圆盘借助A柱移动至C；

那么我们目前的问题就是：如何将n-1个圆盘从A移动到B，再由B移动到C中呢？

此时我们可以将n-1个圆盘看作一个整体：先将n-2个圆盘从A移动到B，将第n-1个圆盘从A移动到C，最后再将B中的n-2个圆盘移动到C中；

此刻问题就化为n-2个圆盘如何从A移动到B再移动到C中？以此类推，最后问题化解为只剩两个圆盘的时候如何移动，此时，结果就变得显而易见了。

代码实现

​
#include<stdio.h>

void mov(int a,int b)
{
	printf("% c--> % c\n", a, b);
}

void hanoi(int n, char a, char b, char c)
{
	if(n<=1)
	mov(a, c);
	else {
		hanoi(n - 1, a, c, b);
		mov(a, c);
		hanoi(n - 1, b, a, c);
	}

}
int main()
{
	int n = 0;
	scanf_s("%d", &n);
	hanoi(n, 'A','B','C');
	return 0;
}

​

运行结果

4
A--> B
A--> C
B--> C
A--> B
C--> A
C--> B
A--> B
A--> C
B--> C
B--> A
C--> A
B--> C
A--> B
A--> C
B--> C