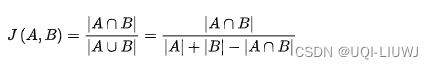1 传统机器学习

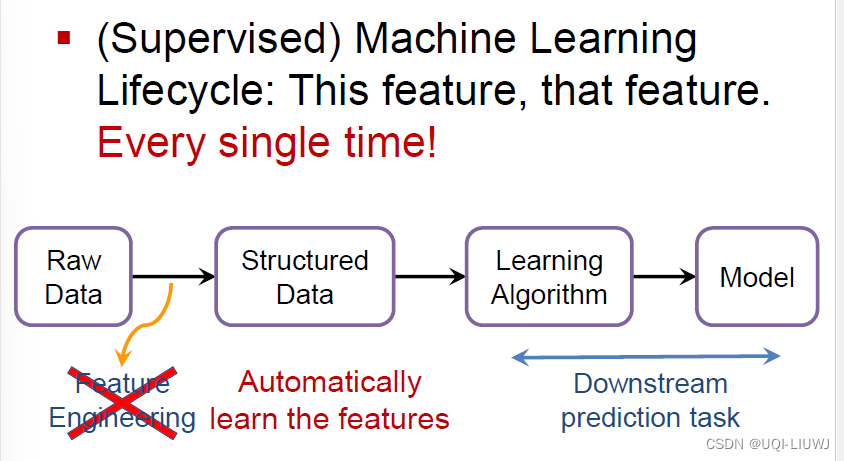
传统机器学习需要进行很多的特征工程
- 我们希望模型自动学习特征，而不是用人为特征工程的方式

1.1 目标

1.2 难点

graph更复杂，CNN和RNN很难直接应用
- ——>复杂的拓扑结构（不像CNN有网格的概念）
- ——>没有固定的节点的顺序，一般情况下也没有参照点（这会导致同构图问题）
- ——>图经常是动态的
- ——>图经常有多模态的特征

2 Node embedding

2.1 目标

将graph上的点嵌入至d维向量，使得相似的点有相近的embedding

2.2 问题配置

图G
节点集合V
邻接矩阵A（在这里假定是0-1矩阵）
不使用其他的信息（比如点特征）

2.3 定义encoder

将点map到embedding上去

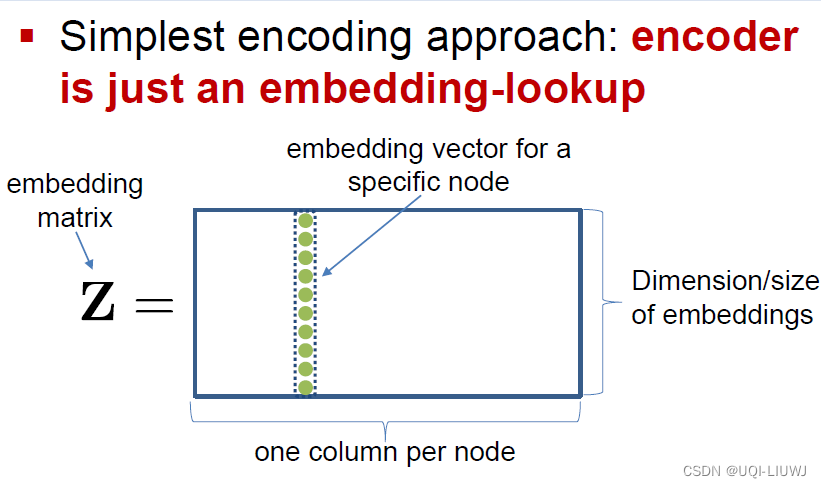
2.3.1 look-up table

一种简单的encoding方式：一张embedding查询表（V是一个one-hot向量）

2.4 定义相似函数

2.4.1 基于邻接的相似度

Ahmed et al. 2013. Distributed Natural Large Scale Graph Factorization .WWW.

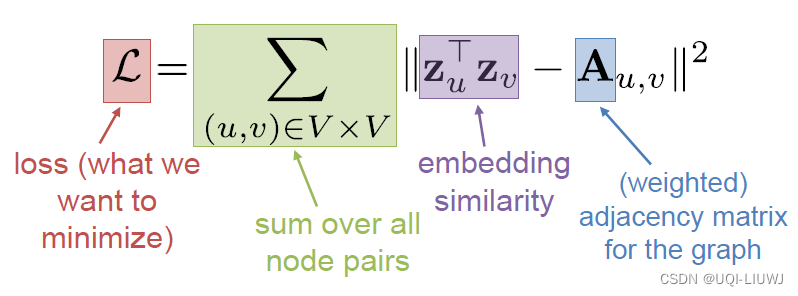
所有点对的相似度和邻接性之间的差异

不足之处

的时间复杂度
- 每一对点都需要考虑一次
- 有些算法可以只考虑有连边的点对，此时复杂度可以降至O(|E|)
O(|V|d)个参数
- 每一个学习的向量（每一个点的向量），都是一个d维向量
只考虑直连边

2.4.2 多跳相似度

•Cao et al. 2015. GraRep : Learning Graph Representations with Global Structural Information . CIKM.

•Ou et al. 2016. Asymmetric Transitivity Preserving Graph Embedding .KDD.

k跳邻居，就是邻接矩阵的k次幂

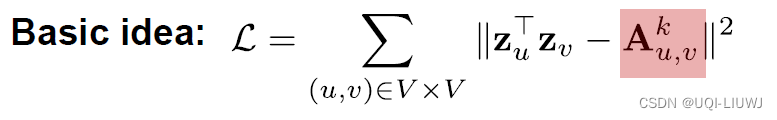
2.4.4 另一种多跳相似度：邻居之间的重合程度

This technique is known as HOPE (Yan et al., 2016).

Asymmetric Transitivity Preserving Graph Embedding

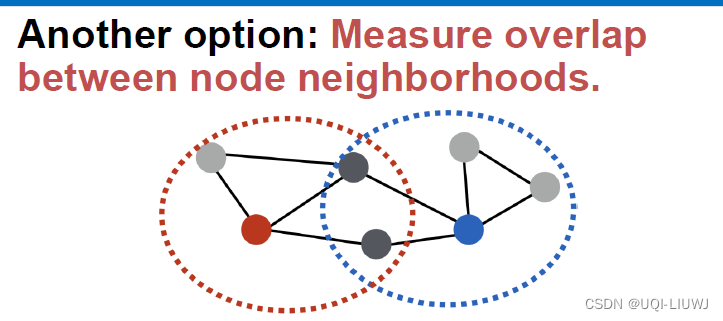
Jaccard similarity
Adamic-Adar score
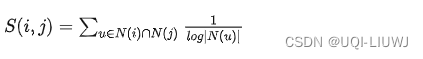
- 这里N(x)表示x的邻居
- 公式表示i，j的共有邻居，每个的邻居数量取log+倒数的和

2.4.5 Random Walk

• Perozzi et al. 2014. DeepWalk : Online Learning of Social Representations . KDD.

• Grover et al. 2016. node2vec: Scalable Feature Learning for Networks . KDD

2.4.5.1随机游走的好处

expressivity：灵活的随机节点相似度定义，这种方法结合了局部和高阶邻域的信息
efficiency：training的时候，不需要考虑所有的点对，只需要考虑在随机游走上同时出现的点对即可

2.4.5.2 随机游走算法

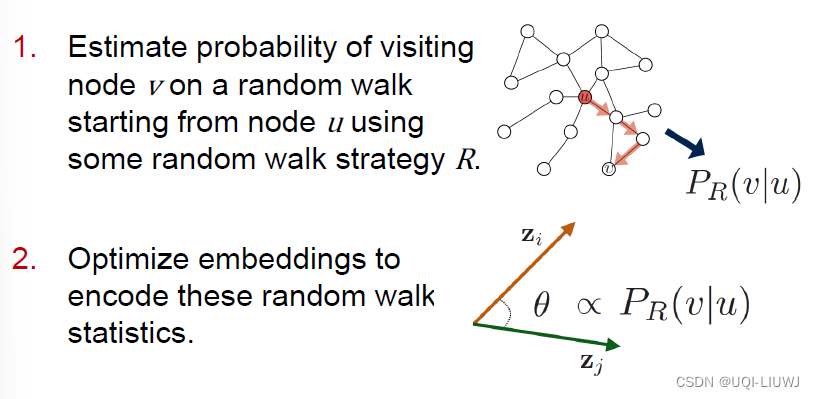
根据某种策略R，从图上的每个点，执行一些随机游走
对图上的每个点u，收集相对应的点集
- $N_R(u)$
  是从u点出来的各条随机游走路径上的点集
- $N_R(u)$
  中可能会有重复的元素
根据对数概率，优化embedding
- 目标：最小化损失函数L
  - ——>最大化在
    $N_R(u)$
    中的v与u之间的
    $log(P(v|Z_u))$
  - ——>最大化在u随机游走路径上的v与u之间的
    $P(v|Z_u)$
  - ——>
    
    在u随机游走路径上的v，尽量地和u相似（
    $Z_u^TZ_v$
    )

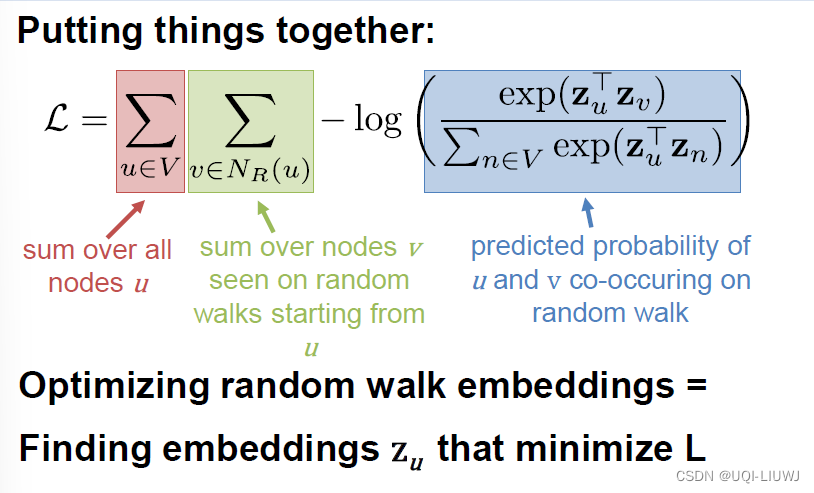
2.4.5.3 随机游走算法优化

上述算法有一个问题，就是我计算
$P(v|Z_u)$
时，分母还是需要每一对node 都计算一边，那么还是
$O(|V|^2)$
的时间复杂度

解决方法：负采样

分母改为随机采样k个点
- 每个点负采样概率正比于这个点的度数

2.4.5.4 随机游走策略

最简单的策略：从每个点跑固定长度，没有bias的随机游走（DeepWalk: Online Learning of Social Representations）

node2Vec：使用灵活的、有bias的随机游走，在网络的局部和整体视图之间进行权衡。

在有bias的随机游走中，需要两个参数

return parameter p

walk away parameter q

他们的作用如下：

从w到s1——>相对于起始点u来说，距离变小了——>离u更近，所以是return

从w到s2——> 相对于起始点u来说，距离不变

从w到s3——>相对于其实点u来说，距离变大了——>离u更远，所以是walk away

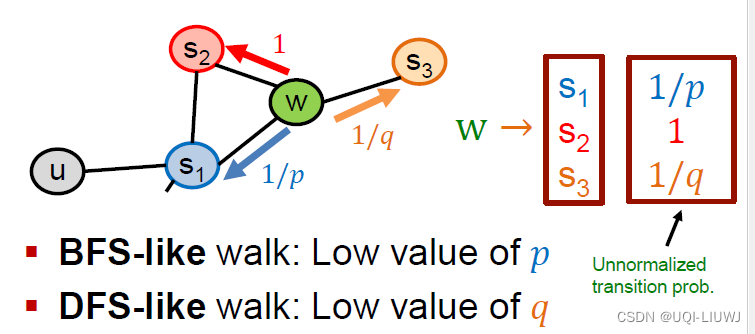
所以如果需要BFS类型的随机游走（围绕在起始点u周围一圈的），那么p值就要小，1/p相应地大，从w到s1的概率就大

如果需要DFS类型的随机游走（从u向远处拓展），那么q值就要小，1/q相应地大，从w到s3的概率就大

其他的一些随机游走

2.5 总结

没有一种方法在所有情况下都是最优的
- Graph Embedding Techniques, Applications, and Performance: A Survey中提到：
  - node2vec在点分类任务中效果更好；
  - multi-hop在边预测任务中效果更好
- 随机游走效率上相对好一些（O(|E|) VS
  $O(|V|^2)$

3 GNN

3.1 配置

图G
节点集V
邻接矩阵A（0-1矩阵）
点特征矩阵
$X \in R^{m \times |V|}$

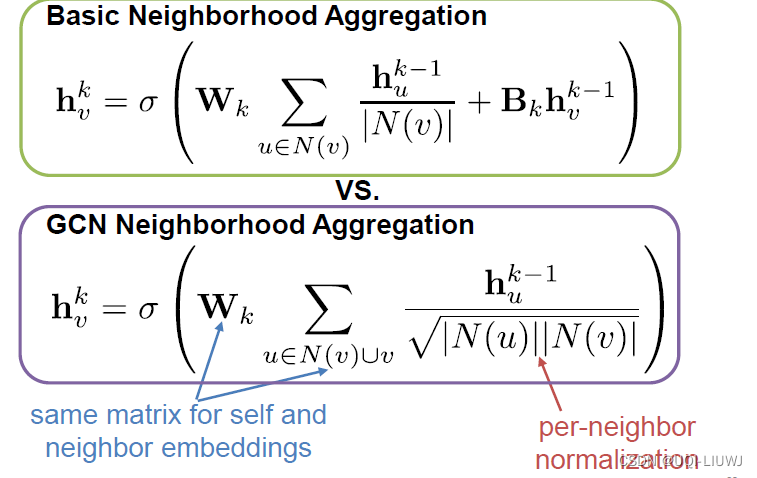
3.2 Neighborhood Aggregation

核心思想是使用类似于神经网络之类的模型将邻居的embedding信息加总到目标点上

不同neighborhood aggregation的区别在于，如何对邻居信息进行整合？

3.2.1 最基本方法：邻居的均值

最基本的方法是：对邻居的信息求平均，然后使用一个神经网络

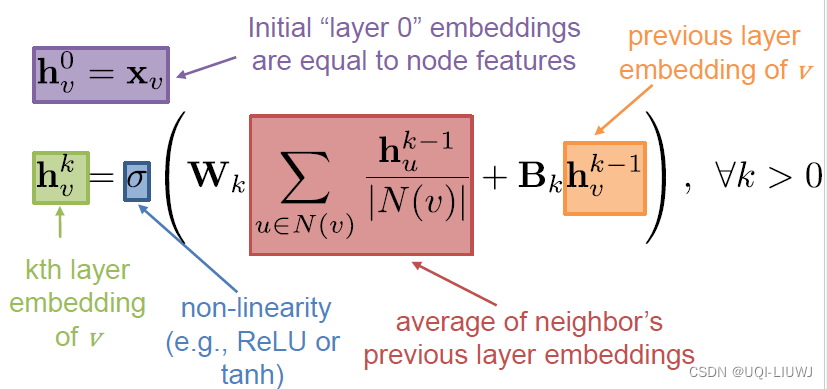
这里Wk和Bk都是可训练的参数

3.2.1.1 好处

这样设计模型的一个好处是，模型的参数Wk和Bk对所有的点都是共享的

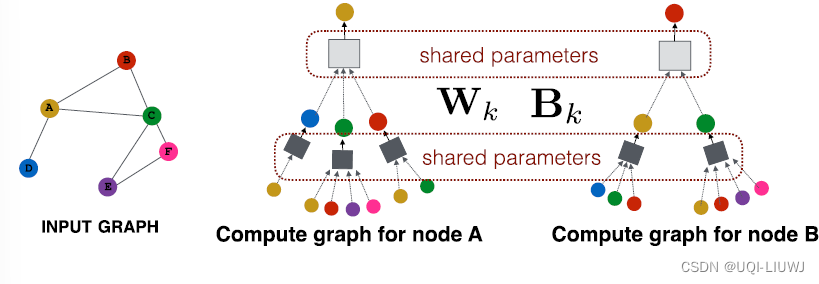
另一个好处是，训练好的模型可以延申到新的graph中去

3.3 GCN

Semi-Supervised Classification with Graph Convolutional Networks

3.3.1 neighborhood aggregation

不是简简单单的平均，这里通过点的度数进行normalization

原文链接：https://blog.csdn.net/qq_40206371/article/details/128257267