海森矩阵(Hessian Matrix)
Key Words: Hessian Matrix, second order derivatives, convexity, and saddle points
原文链接:Hessian, second order derivatives, convexity, and saddle points
翻译:
Hessian Matrix:二阶导和函数曲率
回忆一下
f
f
f的梯度
f
:
R
n
→
R
f:\mathbb{R}^n \rightarrow \mathbb{R}
f:Rn→R:
f
′
(
x
)
=
[
δ
f
δ
x
1
,
δ
f
δ
x
2
,
⋯
,
δ
f
δ
x
n
]
(1)
f'(x) = [\frac{\delta f}{\delta x_1}, \frac{\delta f}{\delta x_2}, \cdots, \frac{\delta f}{\delta x_n} ]\tag{1}
f′(x)=[δx1δf,δx2δf,⋯,δxnδf](1)
求
f
f
f的二阶导意味着,我们可以看到第
i
i
i个一阶导
δ
f
δ
x
i
\frac{\delta f}{\delta x_i}
δxiδf是如何影响其他所有偏导数的。求二阶导相当于求
f
′
(
x
)
f'(x)
f′(x)的Jacobian矩阵,结果如公式(2)所示。
H
=
[
∂
2
f
∂
x
1
2
∂
2
f
∂
x
1
∂
x
2
⋯
∂
2
f
∂
x
1
∂
x
n
∂
2
f
∂
x
2
∂
x
1
∂
2
f
∂
x
2
2
⋯
∂
2
f
∂
x
2
∂
x
n
⋮
⋮
⋱
⋮
∂
2
f
∂
x
n
∂
x
1
∂
2
f
∂
x
n
∂
x
2
⋯
∂
2
f
∂
x
n
2
]
(2)
H=\left[\begin{array}{cccc}{\frac{\partial^{2} f}{\partial x_{1}^{2}}} & {\frac{\partial^{2} f}{\partial x_{1} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f}{\partial x_{1} \partial x_{n}}} \\ {\frac{\partial^{2} f}{\partial x_{2} \partial x_{1}}} & {\frac{\partial^{2} f}{\partial x_{2}^{2}}} & {\cdots} & {\frac{\partial^{2} f}{\partial x_{2} \partial x_{n}}} \\ {\vdots} & {\vdots} & {\ddots} & {\vdots} \\ {\frac{\partial^{2} f}{\partial x_{n} \partial x_{1}}} & {\frac{\partial^{2} f}{\partial x_{n} \partial x_{2}}} & {\cdots} & {\frac{\partial^{2} f}{\partial x_{n}^{2}}}\end{array}\right]\tag{2}
H=⎣⎢⎢⎢⎢⎢⎡∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋱⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f⎦⎥⎥⎥⎥⎥⎤(2)
海森矩阵体现了不同输入维之间相互加速的速率。e.g.:如果
H
1
,
1
H_{1,1}
H1,1 is high,这表明维度1的加速度较高。如果
H
1
,
2
H_{1,2}
H1,2 is high,那么我们在两个维度上均同时加速。如果
H
1
,
2
H_{1,2}
H1,2 是负的,那么当第一个维度加速时,第二个维度在减速。
海森 & 机器学习
在机器学习中的梯度下降法中,二阶导数测量的是损失函数的曲率,而不是单坐标处的斜率(梯度)。因此,有关海森的信息可以帮助我们采取合适的步长,以达到最小。
假定我们有一个代价函数
f
f
f,它的梯度
f
′
(
x
)
<
0
f'(x)<0
f′(x)<0。我们知道
f
f
f在负梯度方向会下降,但不知道的是1)下降速率越来越快? 2)以不变的速率下降?还是 3)下降得很少,且可能上升?这些信息可以通过求二阶导——Hessian Matrix来了解。
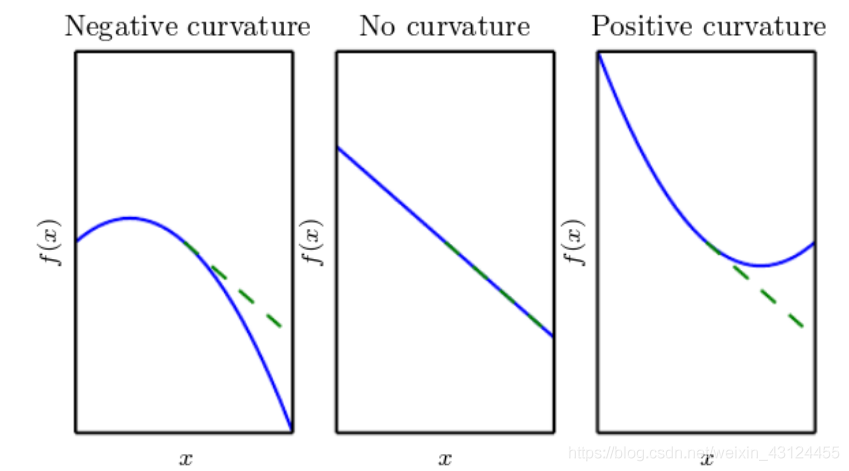
- 图1:
f
′
′
(
x
)
<
0
f”(x)<0
f′′(x)<0,则f
f
f加速下降,最终代价函数的下降幅度将大于梯度乘以步长 - 图2:
f
′
′
(
x
)
=
0
f”(x)=0
f′′(x)=0,函数是一条直线,没有曲率,那么以步长α
\alpha
α沿着负梯度前进,f
f
f就减少c
.
α
.
c. \alpha .
c.α. - 图3:
f
′
′
(
x
)
>
0
f”(x)>0
f′′(x)>0,函数会减速下降,最后会加速上升。因此如果α
\alpha
α太大,梯度下降可能不会使得代价函数达到一个最低点,反而会以一个较高的代价结束这一次计算。
如果我们能够计算二阶导,那么我们就可以选择合适的
α
\alpha
α,从而弱化在局部最小值处的振荡。
特征值、凸性和鞍点
- Hessian的特征向量/特征值描述了主曲率的方向和每个方向的曲率量。
- 如果偏导数是连续的,那么微分的顺序可以换(
∂
2
f
∂
x
1
∂
x
2
=
∂
2
f
∂
x
2
∂
x
1
\frac{\partial^{2} f}{\partial x_{1} \partial x_{2}}=\frac{\partial^{2} f}{\partial x_{2} \partial x_{1}}
∂x1∂x2∂2f=∂x2∂x1∂2f)(Clairaut’s theorem)。因此Hessian矩阵是对称的。在深度学习的环境中,一般都是这种情况,因为我们强迫使我们的函数是连续且可微的。Hessian就可以被分解成一组实特征值和一组正交特征向量。 - 在机器学习优化中,当我们使用梯度下降法收敛到一个临界点后,我们需要检查海森特征值来确定它是最小、最大还是鞍点。研究特征值的性质可以告诉我们函数的凸性。对于所有
x
∈
R
n
\bm x∈R^n
x∈Rn :- 如果H是正定的,
H
≻
0
H \succ 0
H≻0(所有特征值> 0),那么二次型问题在高维空间中呈“碗”形,且严格凸(只有一个全局最小值)。如果f
′
(
x
)
=
0
f'(\bm x)=0
f′(x)=0,那么x
\bm x
x是全局最小值点。 - 如果半正定,
H
⪰
0
H\succeq 0
H⪰0(所有特征值>=0),则函数是凸的,如果f
′
(
x
)
=
0
f'(\bm x)=0
f′(x)=0,则x
\bm x
x是局部最小值点。 - 负正定
H
≺
0
H\prec 0
H≺0(所有特征值<0),二次型问题在高维情况下呈倒碗状,并且是严格凹的(只有一个全局最大值)。如果f
′
(
x
)
=
0
f'(\bm x)=0
f′(x)=0,那么x
\bm x
x就是全局最大值。 - 半负定⪯0(所有特征值< = 0),那么函数是凹的。如果
f
′
(
x
)
=
0
f'(\bm x)=0
f′(x)=0,则x
\bm x
x是局部最大值。 - 如果H是不定的,(在
x
\bm x
x处的特征值有正有负),这意味着x
\bm x
x是局部最小&局部最大,因此x
\bm x
x是f
f
f的一个鞍点。
- 如果H是正定的,
这里n维向量
x
=
(
x
1
,
x
2
,
.
.
.
.
,
x
n
)
\bm x=(x_1,x_2,….,x_n)
x=(x1,x2,....,xn),所以
f
′
(
x
)
=
0
f'(\bm x)=0
f′(x)=0表示对所有自变量
x
i
x_i
xi的偏导数
δ
f
δ
x
i
=
0
\frac{\delta f}{\delta x_i}=0
δxiδf=0。

注意,1~4反推下并不成立。e.g. :严格凸并不意味着正定。
(原文还有个泰勒展开,来证明这个的,不翻译了,看原文即可)