博客

背景

卷积是信号处理中的重要操作，在深度学习中更是重中之重，所以有必要对一些经典的快速卷积方法做一些了解。

在查阅了若干资料后，对于Cook-Toom算法，以下简称CT算法，有了一定的了解，记录一下，便于以后查阅。

卷积介绍

由于这个算法比较经典，所以默认处理的是信号系统中的一维卷积，此文也是基于一维卷积对CT算法做一个介绍。

一维卷积过程如下：

给定信号f[n]以及滤波器g[m]，则卷积过后的信号s[n]长度为N=n+m-1，具体计算为：

s[n]=(f*g)[n] = \sum_{m=-M}^{m=M}f[m]g[n-m]

以3个元素的信号为例：

f(n) = [1 2 3]; g(n) = [2 3 1];

s(0) = f(0)g(0-0) + f(1)g(0-1)+f(2)g(0-2) = 1

2 + 2

0 + 3*0 =2

s(1) = f(0)g(1-0) + f(1)g(1-1) + f(2)g(1-2) = 1

3 + 2

2 + 3*0 = 7

s(2) = f(0)g(2-0) + f(1)g(2-1) + f(2)g(2-2) =1

1 + 2

3 + 3*2=13

s(3) = f(0)g(3-0) + f(1)g(3-1) + f(2)g(3-2) =1

0 + 2

1 + 3*3=11

s(4) = f(0)g(4-0) + f(1)g(4-1) + f(2)g(4-2) =1

0 + 2

0 + 3*1=3

最终结果为:

 s(n) = [2 7 13 11 3]

拉格朗日插值定理

直接从wiki抄过来的，证明过程可以参考

拉格朗日插值法

简单来说就是，对于n+1组二维点，可以找到一个不超过n阶多项式函数，拟合这n+1组点。CT算法就是这个定理在卷积上的应用。

Cook-Toom 算法

一个事实

下面所有和加速有关的解释，都依赖于一个前提：计算平台的乘法比加法慢，且慢的多。根据一般规律，CPU处理乘法的时间，大致上是处理加(减)法的10倍。

也就是说，如果我们去掉一个乘法操作的代价是增加不超过10个加法，理论上是可以提升效率的，但是这个不一定时时刻刻都正确，因为还要考虑到cache，如果是乱序还要考虑流水线等等。总体来说，如果能减少乘法运算，且增加少量的加法运算，被认为是速度上的提升。

CT算法

具体步骤

以2×2的卷积过程为例说明，2×2的卷积会产生2+2-1=3个数，所以需要3个对应点：

• 计算
  
  
  
  s

  (

  β

  i

  )

  s(\beta_i)
  
  
  
  
  
  
  s
  
  
  (
  
  
  
  β
  
  
  
  
  
  
  
  
  
  
  i
  
  
  
  
  
  ​
  
  
  
  
  
  
  
  
  
  
  
  
  )
  
  
  
  
  
  
  

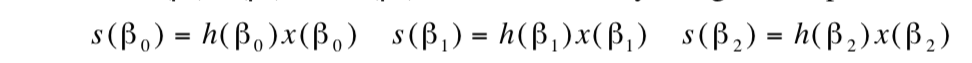
• 计算
  
  
  
  s

  (

  p

  )

  s(p)
  
  
  
  
  
  
  s
  
  
  (
  
  
  p
  
  
  )
  
  
  
  
  
  ：
  
  

• 改写成矩阵形式
  
  

• 实际计算过程：
  
  
  
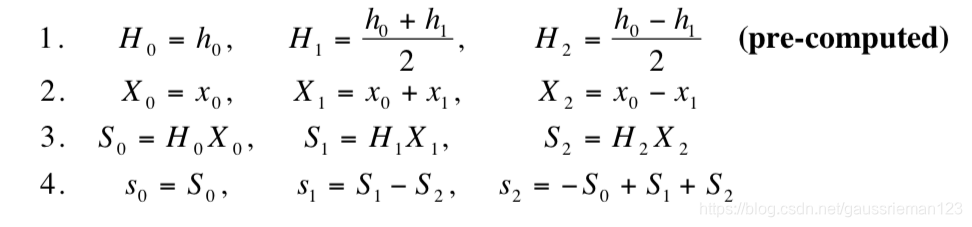
  因为h为滤波器，所以可以提前计算H相关的值，其他值都是需要实时计算，一共包括5次加法和3次乘法，乘法数量就是上面中间矩阵主对角线不为0的值的数量。

评价

Cook-Toom算法能够利用加法来换乘法运算，在某些情况下，可以减少整体的计算时间，而且将卷积计算和多项式乘法有效的结合起来，思路非常值得学习，缺点是当卷积核较大时，增加的加法数量以远超核大小的速度增长，最终会导致增加的加法所耗费的时间甚至超过节省下来的乘法所耗费的时间。

因为CT算法本身是建立在Lagrange之上的，如果要改进这种算法，也可以从Lagrange定理入手，比如使用重心Lagrange插值法等。

参考

https://antkillerfarm.github.io/dl%20acceleration/2019/07/19/DL_acceleration.html

http://people.ece.umn.edu/users/parhi/SLIDES/chap8.pdf

https://zh.wikipedia.org/wiki/拉格朗日插值法