博客

1、算法介绍

ICP（Iterative Closest Point迭代最近点）算法是一种点集对点集配准方法。用数学语言描述如下，即ICP算法的实质是基于最小二乘法的最优匹配，它重复进行“确定对应关系的点集→计算最优刚体变换”的过程，直到某个表示正确匹配的收敛准则得到满足。



ICP算法基本思想：

如果知道正确的点对应，那么两个点集之间的相对变换（旋转、平移）就可以求得封闭解。



首先计算两个点集X和P的质心，分别为μx和μp



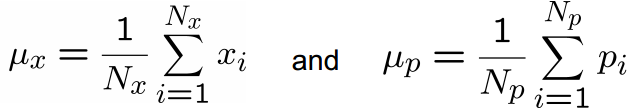
然后在两个点集中分别减去对应的质心（Subtract the corresponding center of mass from every point in the two point sets before calculating the transformation）



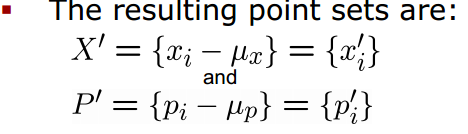
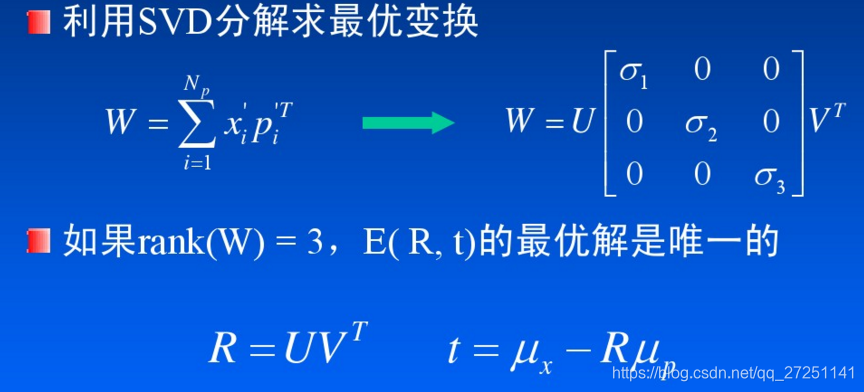
目标函数E(R,t)的优化是ICP算法的最后一个阶段。在求得目标函数后，采用什么样的方法来使其收敛到最小，也是一个比较重要的问题。求解方法有基于奇异值分解的方法、四元数方法等。



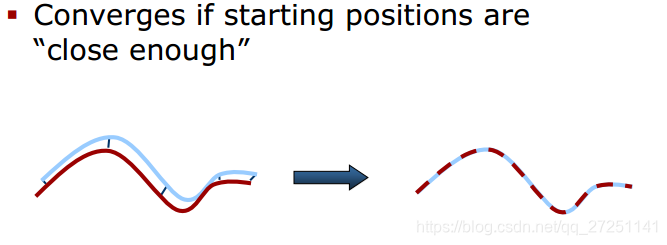
如果初始点“足够近”，可以保证收敛性

2、算法优缺点

ICP算法优点：

可以获得非常精确的配准效果

不必对处理的点集进行分割和特征提取

在较好的初值情况下，可以得到很好的算法收敛性

ICP算法的不足之处：

在搜索对应点的过程中，计算量非常大，这是传统ICP算法的瓶颈

标准ICP算法中寻找对应点时，认为欧氏距离最近的点就是对应点。这种假设有不合理之处，会产生一定数量的错误对应点

3、算法实现

实现代码C++:

#include <iostream>

#include <eigen3/Eigen/Dense>

using namespace std;
using namespace Eigen;
 
#define PI (double)3.141592653589793
void ICP(const vector<Vector3f>& pts1, const vector<Vector3f>& pts2);

// ICP仿真

int main(int argc, char* argv[]) 

{

	Eigen::Vector3f p1_c1(0, 0, 20);

	Eigen::Vector3f p2_c1(2, 4, 30);

	Eigen::Vector3f p3_c1(5, 9, 40);

	Eigen::Vector3f p4_c1(6, 8, 25);

	

	Eigen::AngleAxisf rotation_vector(30 * PI / 180, Eigen::Vector3f(0, 1, 0));//绕y轴逆时针旋转30度(转yaw)

	Eigen::Matrix<float, 3, 3> R21 = rotation_vector.toRotationMatrix();

	cout << "R21: " << endl << R21 << endl;

	Eigen::Vector3f t21(5, 3, 1);

 

	Eigen::Vector3f p1_c2 = R21*p1_c1 + t21;

	Eigen::Vector3f p2_c2 = R21*p2_c1 + t21;

	Eigen::Vector3f p3_c2 = R21*p3_c1 + t21;

	Eigen::Vector3f p4_c2 = R21*p4_c1 + t21;

 

	vector<Vector3f> p_c1, p_c2;

	p_c1.push_back(Vector3f(p1_c1[0], p1_c1[1], p1_c1[2]));

	p_c1.push_back(Vector3f(p2_c1[0], p2_c1[1], p2_c1[2]));

	p_c1.push_back(Vector3f(p3_c1[0], p3_c1[1], p3_c1[2]));

	p_c1.push_back(Vector3f(p4_c1[0], p4_c1[1], p4_c1[2]));

 

	p_c2.push_back(Vector3f(p1_c2[0], p1_c2[1], p1_c2[2]));

	p_c2.push_back(Vector3f(p2_c2[0], p2_c2[1], p2_c2[2]));

	p_c2.push_back(Vector3f(p3_c2[0], p3_c2[1], p3_c2[2]));

	p_c2.push_back(Vector3f(p4_c2[0], p4_c2[1], p4_c2[2]));

 

	ICP(p_c1, p_c2);

 

	getchar();
    return 0;

}

 

void ICP(const vector<Vector3f>& pts1,const vector<Vector3f>& pts2)

{

	Vector3f p1, p2;     // center of mass

	int N = pts1.size();

	for (int i = 0; i<N; i++)

	{

		p1 += pts1[i];

		p2 += pts2[i];

	}

	p1 = Vector3f((p1) / N);

	p2 = Vector3f((p2) / N);

	vector<Vector3f> q1(N), q2(N); // remove the center

	for (int i = 0; i<N; i++)

	{

		q1[i] = pts1[i] - p1;

		q2[i] = pts2[i] - p2;

	}

 

	// compute q1*q2^T

	Eigen::Matrix3f W = Eigen::Matrix3f::Zero();

	for (int i = 0; i<N; i++)

	{

		W += Eigen::Vector3f(q1[i](0), q1[i](1), q1[i](2)) * Eigen::Vector3f(q2[i](0), q2[i](1), q2[i](2)).transpose();

	}

 

	// SVD on W

	Eigen::JacobiSVD<Eigen::Matrix3f> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);

	Eigen::Matrix3f U = svd.matrixU();

	Eigen::Matrix3f V = svd.matrixV();

 

	Eigen::Matrix3f R_12 = U* (V.transpose());

	Eigen::Vector3f t_12 = Eigen::Vector3f(p1(0), p1(1), p1(2)) - R_12 * Eigen::Vector3f(p2(0), p2(1), p2(2));

 

	// 验证

	Eigen::AngleAxisf R_21;

	R_21.fromRotationMatrix(R_12.transpose());

	cout << "aix: " << R_21.axis().transpose() << endl;

	cout << "angle: " << R_21.angle() * 180 / PI << endl;

	cout << "t: " << (-R_12.transpose()*t_12).transpose() << endl;


}