微分变换构造雅可比逆解
注意:雅可比矩阵的构造和逆解的解算,此处只是理论,还需联系实际学习实验。
机器人微分运动原理:
1)机器人运动链中某一连杆对于固定系的位姿为T(T当前),经过微运动后该杆对固定系的位姿变为T+dT(T目标),若这个微运动是相对于固定系进行的,总可以用微小的平移和旋转来表示,即
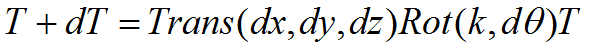
T目*T-1=Trans(dx,dy,dz)*Rot(k,dθ)*T*T-1
Trans(dx,dy,dz)*Rot(k,dθ)=T目*T-1
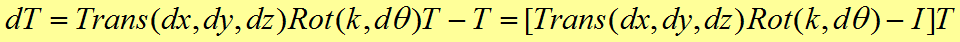
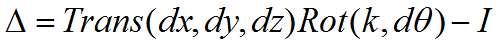
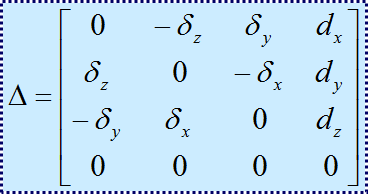
注意:矩阵中各个不同符号代表是相对固定坐标系的的微分运动值(角度或位移量)
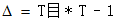
2)若微分运动是相对于某个杆系{i}进行的,则T+dT可以表示为
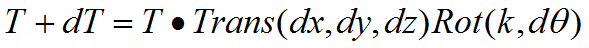
T-1*T目=T-1*T*Trans(dx,dy,dz)*Rot(k,dθ)
Trans(dx,dy,dz)*Rot(k,dθ)=T-1*T目
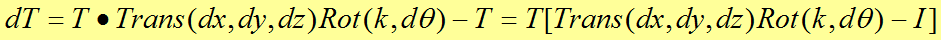
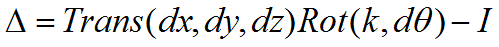
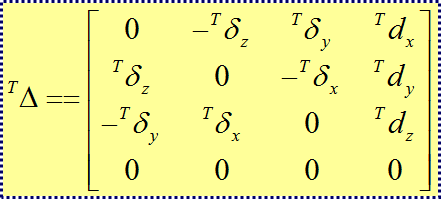
注意:矩阵中左上角的T代表是相对坐标系T的微分运动值(角度或位移量)
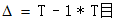
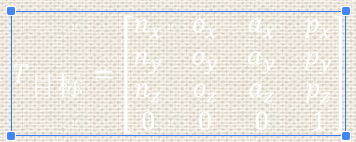
1.目标矩阵:
2.根据当前各个关节角度,计算当前位姿矩阵T
3.由当前位姿和目标位姿计算微分运动矩阵:
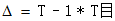
对于任一给定的坐标系T的微分运动矩阵:(矩阵中左上角的T代表是相对坐标系T的微分运动值)
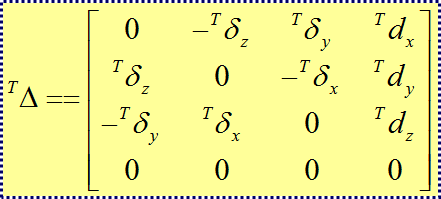


4.根据微分运动矩阵,可以得到关节的微分运动D:
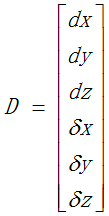
5.构建雅可比矩阵:
a.计算各连杆变换
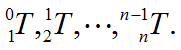
b.计算各连杆至末端连杆的变换
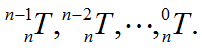
c.计算J(q)的各列元素,第i列
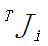
由
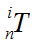
所决定。
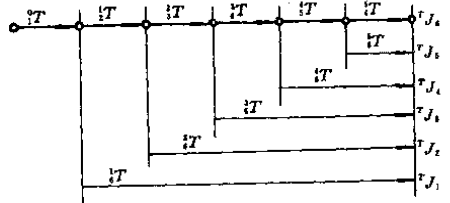
若该关节为移动关节:
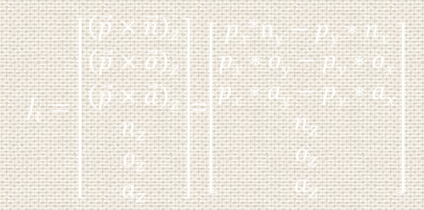
6.根据雅可比矩阵,将一个坐标系内位置和姿态的微小变化变换为机器人手坐标系的位置和姿态的微小变化。
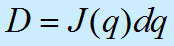
即:
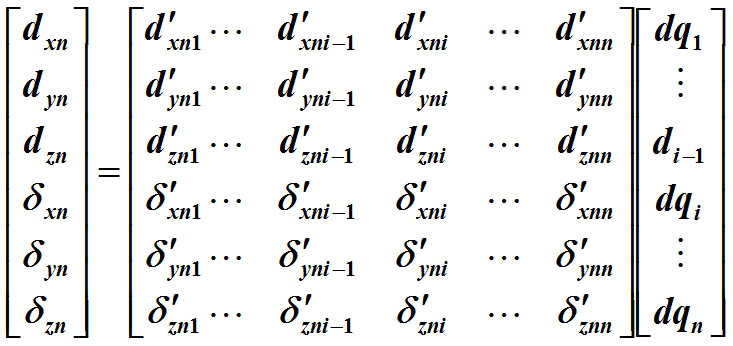
7.关节变量=J(q)-1*D
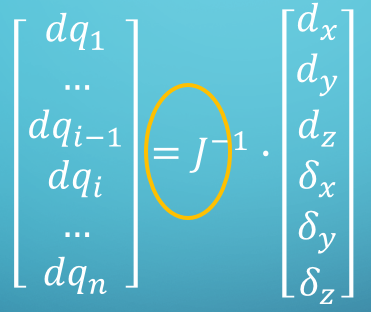
注意:雅克比矩阵非满秩则无逆矩阵,故用svd分解求伪逆代替
8.设置阈值η和迭代次数N,进行迭代
1)当关节变量每个值的绝对值都小于η(η是满足精度需要的自定义小数)时,迭代结束,并输出当前各个关节值。
2)当迭代次数>N(N为满足预计迭代次数要求的自定义充分大数)时,迭代结束,并输出迭代失败信息
3)当关节变量>η且迭代次数小于N时,令θcur=θcur+dθ,并计算Tcur=Tθcur
9.重复2到8步骤,直至迭代退出条件满足