一、题目

给定一个 没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]

输出:

[

[1,2,3],

[1,3,2],

[2,1,3],

[2,3,1],

[3,1,2],

[3,2,1]

]

二、思路

深度优先搜索(DFS) + 回溯

：

“回溯”可以理解为“状态重置”，就是回到上一步的状态。通常，我们要解决的问题是在一棵树上完成的，在这棵树上搜索需要的答案，一般使用深度优先搜索。

以数组 [1, 2, 3] 为例进行分析。

我们自己手写的话，只需要按顺序枚举每一位可能出现的情况，已经选择过的数字不能再使用，即

• 在枚举第一位的时候，有三种情况；
• 在枚举第二位的时候，前面已经用过的数字不能再用，此时只有两种情况；
• 在枚举第三位的时候，前面两个已经用过的数字不能再用，此时只有一种情况。

这样就能做到不重不漏，把可能的全排列都枚举出来，结果如下图所示：



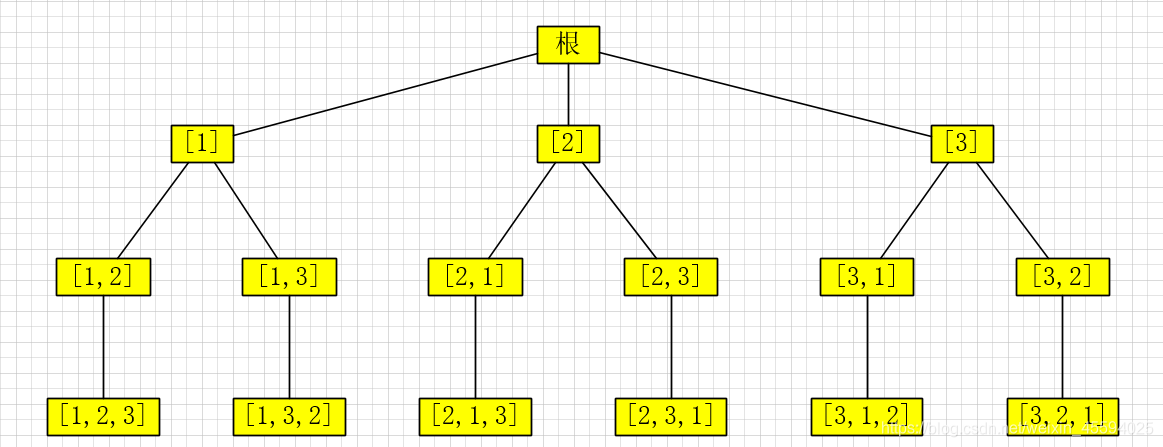
如上图，将所有的结果写出来，用一个树形结构表示，就是这个问题的

解空间树

。每执行一次深度优先搜索，从树的根节点到叶节点的路径就是一个全排列。使用回溯法搜索全排列的解的过程如下图：




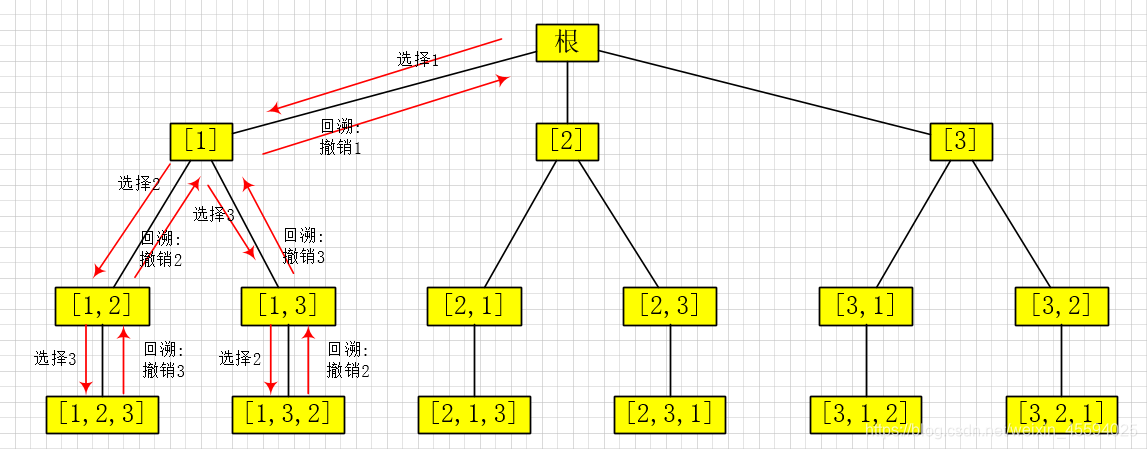
说明：

• 每一个节点表示全排列问题求解的不同阶段，也叫状态；
• 深度优先搜索的过程中，在搜索至叶节点时需要回溯，即返回上一步继续求解，这时的状态变量需要设置成为和先前一样；
• 因此，在回溯到上一层节点时，需要撤销上一次选择，即“状态重置”；
• 上图中，在 [1, 2] 处撤销 2 回到了 [1]，又选择了 3 到达了状态 [1, 3]，因为上一步撤销了 2，所以在这里才可以选择 2 从而达到状态 [1, 3, 2]，这就是状态重置的意义。

三、代码

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> list = new ArrayList<>();
        backTrack(list, new ArrayList<Integer>(), nums);
        return list;
    }

    public void backTrack(List<List<Integer>> list, List<Integer> tempList, int[] nums){
        if(tempList.size() == nums.length){
            list.add(new ArrayList<>(tempList));
        }else{
            for(int i = 0; i < nums.length; i++){
            	// 已经使用过的数字就不能再用了，continue跳出本次循环，进行下一次循环
                if(tempList.contains(nums[i]))
                    continue;
                tempList.add(nums[i]);
                backTrack(list, tempList, nums);
                tempList.remove(tempList.size() - 1);// 回溯到上一步
            }
        }
    }
}