Paper :
GRAPH ISOMORPHISM NETWORK
Code :
摘要
作者使用Weisfeiler-Lehman(WL) test 和同构图判定问题来评估GNN网络的表达能力,并提出了GIN网络结构,理论分析GIN的表达能力优于GraphSAGE GCN等结构,在多任务上准确率达到了SOTA。WL测试与GNN具有相似的信息传递方式,在WL test算法运行的过程中,算法构造了从 multiset 到 representation 的单射函数,因此WL test在图同构问题上具有强表达能力。作者尝试使用GNN构造与WL test 在图同构问题上相同强度的表达能力的网络结构。
本文的贡献主要有以下四点
- 证明GNN在图同构问题上至多与WL test 表达能力相同
- 提出了GNN与WL test 表达能力相同时,需要满足的聚合表达式和图读出函数的条件
- 给出了GCN GraphSAGE 等网络区分不了的网络结构特例
- 提出了GIN网络结构
准备
通用GNN网络的数学表示可以使用如下形式
a
v
(
k
)
=
Aggregate
(
k
)
(
{
h
u
(
k
−
1
)
∣
u
∈
N
(
v
)
}
)
h
v
(
k
)
=
Combine
(
k
)
(
h
v
(
k
−
1
)
,
a
v
(
k
)
)
\\a_{v}^{(k)} = \text{Aggregate}^{(k)}(\{h_{u}^{(k-1)}|u\in N(v)\}) \\h_{v}^{(k)} = \text{Combine}^{(k)}(h_v^{(k-1)},a_v^{(k)})
a
v
(
k
)
=
Aggregate
(
k
)
(
{
h
u
(
k
−
1
)
∣
u
∈
N
(
v
)
}
)
h
v
(
k
)
=
Combine
(
k
)
(
h
v
(
k
−
1
)
,
a
v
(
k
)
)
其中
h
v
(
k
)
h_{v}^{(k)}
h
v
(
k
)
是第k个迭代层中节点v的特征向量。我们初始化
h
v
(
0
)
=
X
v
h_v^{(0)} = X_v
h
v
(
0
)
=
X
v
对于GraphSAGE网络,上式表示为
a
v
(
k
)
=
max
(
{
ReLU
(
W
(
k
)
h
u
(
k
−
1
)
)
∣
u
∈
N
(
v
)
}
)
h
v
(
k
)
=
W
′
(
k
)
(
h
v
(
k
−
1
)
∣
∣
a
v
(
k
)
)
\\a_{v}^{(k)} = \max(\{\text{ReLU}(W^{(k)}h_{u}^{(k-1)})|u\in N(v)\}) \\h_{v}^{(k)} = W’^{(k)}(h_{v}^{(k-1)}||a_v^{(k)})
a
v
(
k
)
=
max
(
{
ReLU
(
W
(
k
)
h
u
(
k
−
1
)
)
∣
u
∈
N
(
v
)
}
)
h
v
(
k
)
=
W
′
(
k
)
(
h
v
(
k
−
1
)
∣
∣
a
v
(
k
)
)
对于GCN,上式表示为
h
v
(
k
)
=
ReLU
(
W
(
k
)
Mean
{
h
u
(
k
−
1
)
∣
u
∈
N
(
v
)
∪
{
v
}
}
)
\\h_{v}^{(k)} = \text{ReLU}(W^{(k)}\text{Mean}\{h_{u}^{(k-1)}|u\in N(v)\cup\{v\}\})
h
v
(
k
)
=
ReLU
(
W
(
k
)
Mean
{
h
u
(
k
−
1
)
∣
u
∈
N
(
v
)
∪
{
v
}
}
)
当进行图分类任务时,需要将点特征转化为全局特征
h
G
=
Readout
(
{
h
v
(
K
)
∣
v
∈
V
}
)
h_G = \text{Readout}(\{h_v^{(K)}|v\in V\})
h
G
=
Readout
(
{
h
v
(
K
)
∣
v
∈
V
}
)
WL test:迭代式,用于解决图同构问题的算法,包含以下两步
- 聚合节点及其邻域的标签
- 将聚合后的标签散列为唯一的新标签
如果在某些迭代中两个图之间的节点的标签不同,则该算法确定两个图是非同构的。一个WL test 的例子如下所示
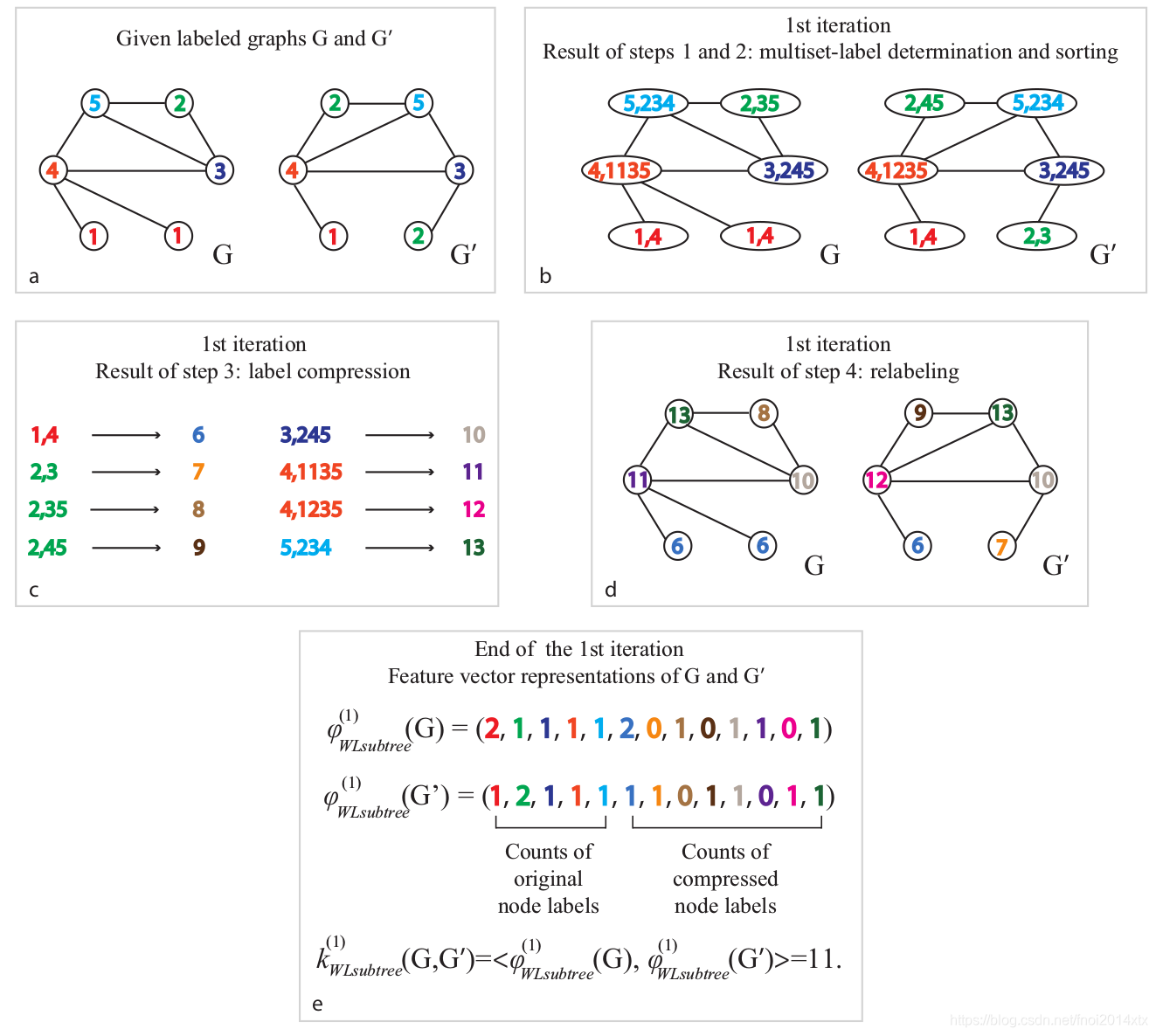
如果将散列后的节点按照在图中出现的次数排成一个一维向量,该向量(WL subtree kernel)可以用来衡量两张图之间的相似度。
理论分析
在以下的理论分析中,假定节点上的特征是来源于可数空间的,假定GNN每层的输出特征也是来自可数空间的。这样,可以将每种特征表示映射到一个整数标签
{
a
,
b
,
c
.
.
.
}
\{a,b,c…\}
{
a
,
b
,
c
.
.
.
}
上。
可重复集合(MultiSet):
X
=
(
S
,
m
)
X = (S,m)
X
=
(
S
,
m
)
其中,
S
S
S
表示集合中每种元素,
m
m
m
给出不同种对应的出现次数。
通过研究GNN何时将两个节点映射到相同的特征表示来研究GNN的表示能力,表示能力的理论上限为当两个节点对应的子树相同时,才映射到相同的特征表示。子树的定义如下

而GNN的聚合操作可以抽象为将节点对应的multiset映射到特征表示上,显然,当且仅当该映射是单射时GNN具有最强的特征表示能力。
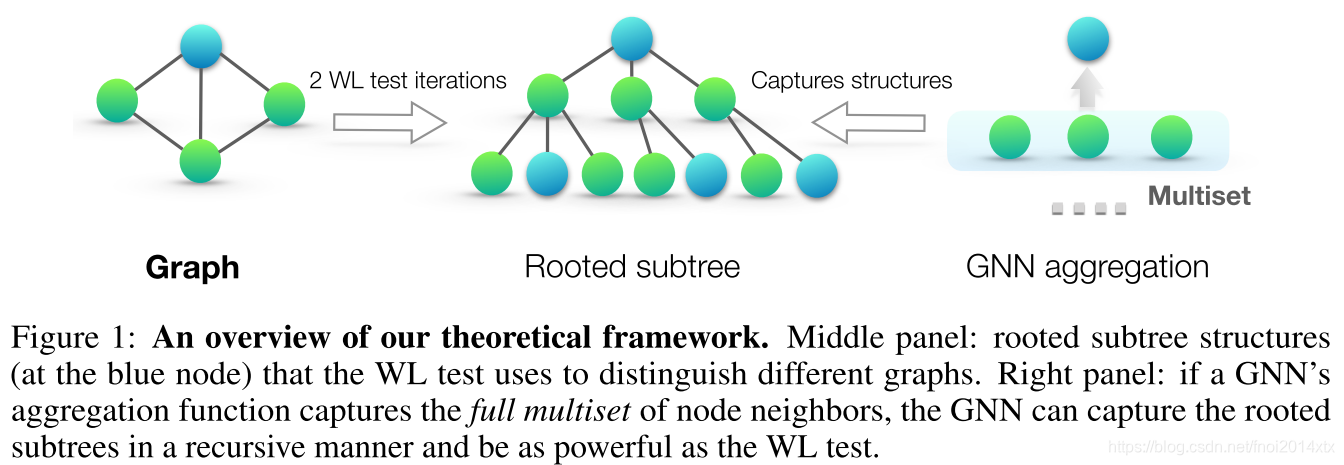
结论1:令两个图
G
1
,
G
2
G_1,G_2
G
1
,
G
2
是任意两个非同构的图。如果存在一个图神经网络
A
:
G
→
R
d
\mathcal{A}: \mathcal{G} \rightarrow \mathbb{R}^{d}
A
:
G
→
R
d
将图
G
1
,
G
2
G_1,G_2
G
1
,
G
2
映射到不同的graph embedding。那么通过Weisfeiler-Lehman同构测试也可以确定非同构性。
结论1说明,在图同构问题上,GNN的理论上限就是WL test。
结论2:令
A
:
G
→
R
d
\mathcal{A}: \mathcal{G} \rightarrow \mathbb{R}^{d}
A
:
G
→
R
d
是一个GNN,对于两个通过Weisfeiler-Lehman同构测试测定为不同构的两个图
G
1
,
G
2
G_1,G_2
G
1
,
G
2
,在GNN层足够多的情况下,如果下面的情况成立,则通过GNN可以将这两个图映射到不同的graph embedding
-
A\mathcal A
A
用下面的公式迭代的聚合和更新节点特征:
hv
(
k
)
=
ϕ
(
h
v
(
k
−
1
)
,
f
(
{
h
u
(
k
−
1
)
:
u
∈
N
(
v
)
}
)
)
h_{v}^{(k)}=\phi\left(h_{v}^{(k-1)}, f\left(\left\{h_{u}^{(k-1)}: u \in \mathcal{N}(v)\right\}\right)\right)
h
v
(
k
)
=
ϕ
(
h
v
(
k
−
1
)
,
f
(
{
h
u
(
k
−
1
)
:
u
∈
N
(
v
)
}
)
)
其中函数
ff
f
作用在multiset上,满足
ϕ\phi
ϕ
函数是单射的 -
读出层作用在multiset
{h
v
(
k
)
}
\{h_{v}^{(k)}\}
{
h
v
(
k
)
}
上,也是单射的
结论3给出了对于图同构问题,如何构造理论表达能力最强的GNN。
结论4:输入的特征空间
X
X
X
是可数的,那么GNN网络中的第
k
k
k
层的输出,
h
v
(
k
)
h_v^{(k)}
h
v
(
k
)
也是可数的
这一结论保证了我们可以将GNN等价到WL test 进行考虑。
GIN
结论5:假定点特征
X
\mathcal X
X
是可数的,存在函数
f
:
X
→
R
n
f :\mathcal{X}\rightarrow \mathbb R^{n}
f
:
X
→
R
n
使得
h
(
X
)
=
∑
x
∈
X
f
(
x
)
h(X) = \sum_{x\in X}f(x)
h
(
X
)
=
∑
x
∈
X
f
(
x
)
是个单射,而且任何定义在multiset上的函数
g
g
g
可以表示成
g
(
X
)
=
ϕ
(
∑
x
∈
X
f
(
x
)
)
g(X) = \phi(\sum_{x\in X}f(x))
g
(
X
)
=
ϕ
(
∑
x
∈
X
f
(
x
)
)
结论6:假定点特征
X
\mathcal X
X
是可数的,存在函数
f
:
X
→
R
n
f :\mathcal{X}\rightarrow \mathbb R^{n}
f
:
X
→
R
n
使得对于无穷多个
ϵ
\epsilon
ϵ
,包含所有无理数
h
(
c
,
X
)
=
(
1
+
ε
)
f
(
c
)
+
∑
x
∈
X
f
(
x
)
h(c,X) = (1+\varepsilon)f(c)+\sum_{x\in X} f(x)
h
(
c
,
X
)
=
(
1
+
ε
)
f
(
c
)
+
x
∈
X
∑
f
(
x
)
是单射函数,其中
c
∈
X
c\in\mathcal X
c
∈
X
而
X
⊂
X
X\subset \mathcal X
X
⊂
X
表示multiset对应的特征集合,而且任何函数
g
g
g
都可以表示为
g
(
c
,
X
)
=
ϕ
(
(
1
+
ε
)
f
(
c
)
+
∑
x
∈
X
f
(
x
)
)
g(c,X) = \phi((1+\varepsilon)f(c)+\sum_{x\in X} f(x))
g
(
c
,
X
)
=
ϕ
(
(
1
+
ε
)
f
(
c
)
+
x
∈
X
∑
f
(
x
)
)
使用MLP来拟合
f
,
g
f,g
f
,
g
,因此,GIN的点特征更新函数表示为
h
v
(
k
)
=
MLP
(
k
)
(
(
1
+
ε
(
k
)
)
h
v
(
k
−
1
)
+
∑
u
∈
N
(
v
)
h
u
(
k
−
1
)
)
h_v^{(k)} = \text{MLP}^{(k)}((1+\varepsilon^{(k)})h_v^{(k-1)}+\sum_{u\in N(v)}h_u^{(k-1)})
h
v
(
k
)
=
MLP
(
k
)
(
(
1
+
ε
(
k
)
)
h
v
(
k
−
1
)
+
u
∈
N
(
v
)
∑
h
u
(
k
−
1
)
)
其中
ε
(
k
)
\varepsilon^{(k)}
ε
(
k
)
是定值或是可学习的。
Graph Embedding构造方法为
h
G
=
∣
∣
k
=
1
K
ReadOut
(
{
h
v
(
k
)
∣
v
∈
G
}
)
h_G = ||_{k=1}^K \text{ReadOut}(\{h_v^{(k)}|v\in G\})
h
G
=
∣
∣
k
=
1
K
ReadOut
(
{
h
v
(
k
)
∣
v
∈
G
}
)
如果
R
e
a
d
O
u
t
ReadOut
R
e
a
d
O
u
t
使用Sum,那么可以转化为 WL test 算法。
GraphSAGE 与 GCN
作者给出了使用Mean和Max进行信息聚合表现不好的例子
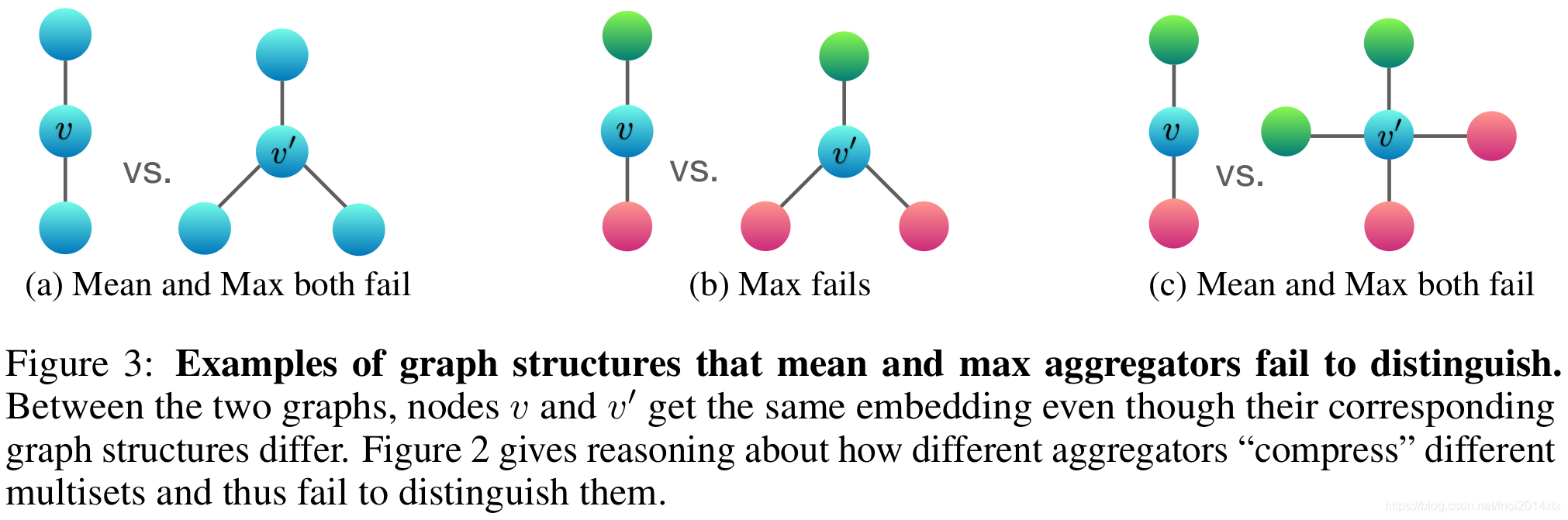
结论:由于mean和max函数 不满足单射性,无法区分某些结构的图,故性能会比sum差。
sum, mean, max 分别可以捕获的信息特点
- sum:学习全部的标签以及数量,可以学习精确的结构信息
- mean:学习标签的比例(比如两个图标签比例相同,但是节点有倍数关系),偏向学习分布信息
- max:学习最大标签,忽略多样,偏向学习有代表性的元素信息

实验结果
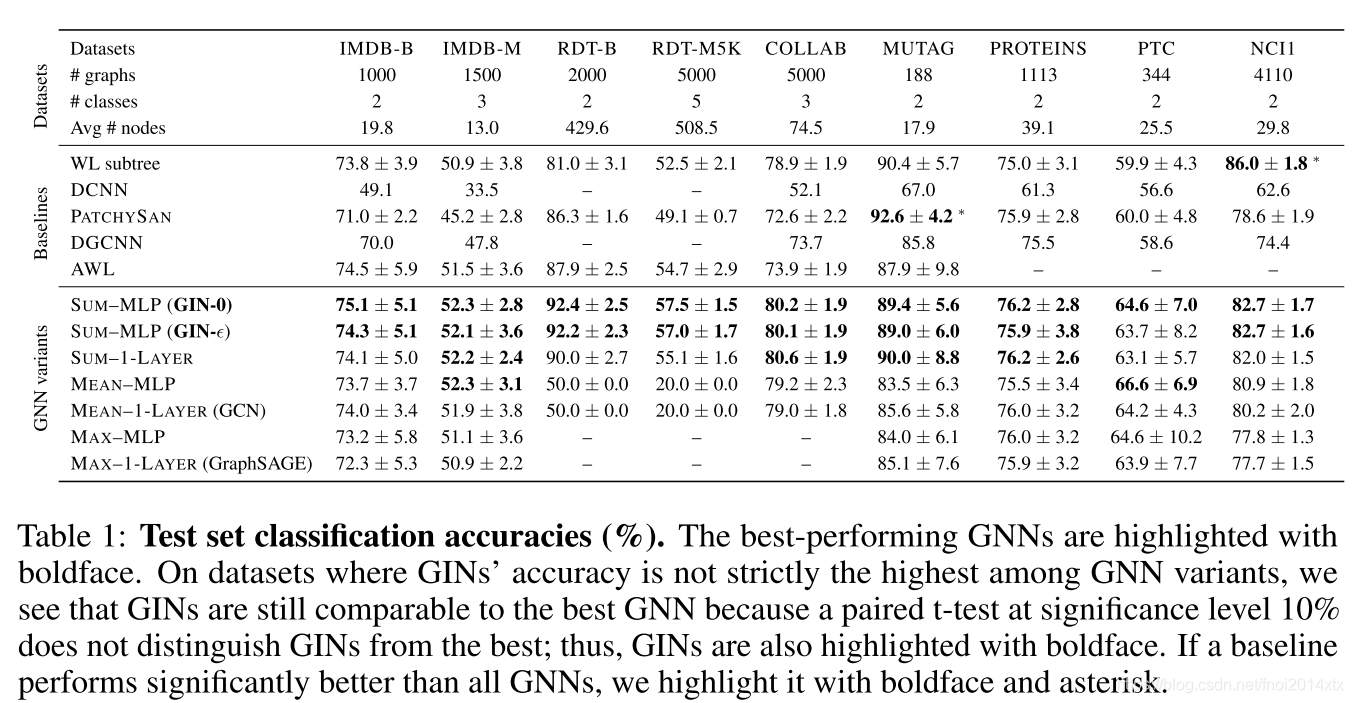
首先,GIN,尤其是GIN-0(固定
ϵ
=
0
\epsilon = 0
ϵ
=
0
),在所有9个数据集上达到了SOTA。 GIN在包含相对大量训练图的社交网络数据集上表现亮眼。对于Reddit数据集,所有节点都与节点要素共享相同的标量。在这里,GIN和求和聚合GNN准确捕获图结构并明显优于其他模型。但是,均值聚合GNN无法捕获未标记图的任何结构,并且其性能也不比随机猜测好。即使提供节点度作为输入特征,基于均值的GNN的效果也要比基于求和的GNN差得多。比较GIN(GIN-0和GIN-
ϵ
\epsilon
ϵ
),我们观察到GIN-0略微但始终优于GIN-
ϵ
\epsilon
ϵ
。由于两个模型均能很好地拟合训练数据,因此与GIN-
ϵ
\epsilon
ϵ
相比,其简单性可以解释GIN-0具有更好的泛化能力。
总结
本文的理论分析建立在两个前提下,第一个是图同构,第二个是图分类任务。不一定可以简单的将其泛化到点分类或其他任务上,需要进行更多的分析和实验。