现有一些用于加速GNN的算法,基本思路是使用mini-batch来计算,用min-batch的梯度估计full-batch的梯度,通过多次迭代达到基本一致的效果。
根据使用的方法不同,
大致分为以下三类
:
-
Neighbor sampling
-
Layer-wise sampling
-
Subgraph sampling
1. Neighbor sampling
1.1 GraphSage
论文标题:Inductive Representation Learning on Large Graphs
论文来源:NIPS2017
论文方向:图表示学习
论文链接:https://arxiv.org/abs/1706.02216

GraphSAGE 是 2017 年提出的一种图神经网络算法,解决了 GCN 网络的局限性: GCN 训练时需要用到整个图的邻接矩阵,依赖于具体的图结构,一般只能用在直推式学习 Transductive Learning。GraphSAGE 使用多层聚合函数,每一层聚合函数会将节点及其邻居的信息聚合在一起得到下一层的特征向量,GraphSAGE 采用了节点的邻域信息,不依赖于全局的图结构。
GraphSAGE 的运行流程如上图所示,可以分为三个步骤:
1、对图中每个顶点邻居顶点进行采样;
2、根据聚合函数聚合邻居顶点蕴含的信息;
3、得到图中各顶点的向量表示供下游任务使用;

出于对计算效率的考虑,对每个顶点采样一定数量的邻居顶点作为待聚合信息的顶点。设采样数量为k,若顶点邻居数少于k,则采用有放回的抽样方法,直到采样出k个顶点。若顶点邻居数大于k,则采用无放回的抽样。
即为每个结点均匀地抽样固定数量的邻居结点,使用Batch去训练。
复杂度正比于卷积层数L
的指数。
1.2
ScalableGCN
阿里的Euler中使用的加速算法,主要思想是用空间换时间。对于N阶GCN模型,开辟存储空间:
![]()
,将mini-batch SGD中各顶点最新的前阶embedding存储起来,前向Aggregate的时候直接查询缓存。
同时也开辟存储空间
![]()
,来存储
![]()
,根据链式法则来获得参数梯度从而更新W。


我们在两个开源的数据集Reddit和PPI上验证了我们的工作。由于GraphSAGE的简单和通用性,我们选择其为baseline。并且为了对齐与其论文中的实验结果,我们在共享了GraphSAGE和ScalableGCN代码中的大多数模块,并利用Tensorflow中的Variable存储
![]()
和
![]()
,使用累加作为算子。
我们使用均匀分布来初始化
![]()
,并将
![]()
初始化为0。对于每阶的卷积操作,我们采样10个邻接顶点。所有的实验均使用512的batch size训练20个epoch。在评估阶段,我们统一维持GraphSAGE的方法进行Inference。以下是选择Mean作为AGG函数的micro-F1 score:
PPI:
| 层数 | 算法 | Micro-F1 |
|---|---|---|
| 1层 | GraphSAGE | 0.47196 |
| 2层 | GraphSAGE | 0.58476 |
| 2层 | ScalableGCN | 0.57746 |
| 3层 | GraphSAGE | 0.63796 |
| 3层 | ScalableGCN | 0.63402 |
Reddit:
| 层数 | 算法 | Micro-F1 |
|---|---|---|
| 1层 | GraphSAGE | 0.91722 |
| 2层 | GraphSAGE | 0.94150 |
| 2层 | ScalableGCN | 0.93843 |
| 3层 | GraphSAGE | 0.94816 |
| 3层 | ScalableGCN | 0.94331 |
可以看到ScalableGCN训练出来模型与GraphSAGE的训练结果相差很小,同时可以取得多层卷积模型的收益。
在时间上,以下是8 core的机器上Reddit数据集(23万顶点)每个mini-batch所需的训练时间:
| 1层 | GraphSAGE | 0.013 |
| 2层 | GraphSAGE | 0.120 |
| 2层 | ScalableGCN | 0.026 |
| 3层 | GraphSAGE | 1.119 |
| 3层 | ScalableGCN | 0.035 |
注意到ScalableGCN的训练时间相对于卷积模型层数来说是线性的。
总结:
GCN是目前业界标准的网络图中特征抽取以及表示学习的方法,未来在搜索、广告、推荐等场景中有着广泛的应用。多阶的GCN的支持提供了在图中挖掘多阶关系的能力。ScalableGCN提出了一种快速训练多阶GCN的方法,可以有效的缩短多阶GCN的训练时间,并且适用于大规模的稀疏图。本方法与对采样进行裁剪和共享的方法也并不冲突,可以同时在训练中使用
1.3 VR-GCN
论文标题:Stochastic Training of Graph Convolutional Networks with Variance Reduction
论文来源:ICML2018
论文方向:图卷积网络
论文链接:
https://arxiv.org/abs/1710.10568
主要思路:
利用结点历史表示
![]()
来作为控制变量(control variate)来减小方差,从而减小batch training中的采样邻居的数量。
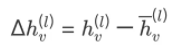
使用蒙特卡方法来洛近似
![]()
,而
![]()
上的平均计算是可接受的(不用递归)。
因此其矩阵表示为:
![]()
该算法具有理论保障,可以获得0偏差和0方差的结果,且无论每层邻居结点的抽样个数 是多少,都不影响 GCN收敛到局部最优。(理论细节请看原文,较为复杂,不展开)
因此每个结点仅仅采样两个邻居,极大提升模型训练效率的同时,也能保证获得良好的模型效果。
2. Layer-wise sampling
2.1 FastGCN
论文标题:FastGCN: fast learning with graph convolutional networks via importance sampling
论文来源:ICLR2018
论文方向:图卷积网络
论文链接:https://arxiv.org/abs/1801.10247
我们已知,GCN的形式为:

从积分的角度看待图卷积,假设图是无限大图的子集,所有结点为独立同分布的结点,满足
![]()

则可以应用蒙特卡洛法,对每一层进行采样 个结点, 来近似积分,以前层的结点作为共享邻居集合:

此外为了减少估计方差(Variance Reduction),采用重要性采样(Importance samling),结点根据以下概率分布采样:


2.2 ASGCN
论文标题:Adaptive Sampling Towards Fast Graph Representation Learning
论文来源:NIPS2018
论文方向:图卷积网络
论文链接:https://arxiv.org/abs/1809.05343

对FastGCN的最后一个公式,其最优的解(最小化从q抽样出的结点的方差,
![]()
)为:

其中
![]()
,而
![]()
则是上一层结点从邻居聚集而来的隐层表示。在FastGCN中,则有
![]()
为了防止递归困境,为importance sampling学习一个独立的决定其重要性的函数(Adaptive sampling),基于结点的特征x(u)来计算:
![]()
因此最终的抽样结点的分布为:

3.Subgraph sampling
3.1 cluster-GCN论文标题:Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks
论文来源:KDD2019
论文方向:图卷积网络
论文链接:https://arxiv.org/abs/1905.07953

主要思路:
为了限制邻居数量的扩张和提高表示的效用,将图分割成多个cluster(限制子图的规模),在cluster上进行结点的batch training。
使用METIS进行图分割,使得cluster内的边多,cluster之间的边少。

具体来说,对于图G分割成c个部分,
![]()
,Vc由第t个分割中的结点构成,Ec仅由Vc中结点之间的边构成,故有 c个子图:
![]()
因此,邻居矩阵可以分为 的子矩阵:
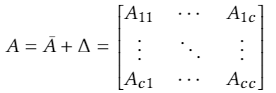

同理也可以对结点特征矩阵X和 Y进行分割,
![]()
。

Loss可以分解为:

两种训练方式:
1.随机挑选一个cluster进行训练(coarse clustering)
2.随机挑选 k 个cluster,然后连接他们再进行训练(stochastic multiple clustering)
3.2 GraphSAINT
论文标题:GraphSAINT: Graph Sampling Based Inductive Learning Method
论文来源:ICLR2020
论文方向:图卷积网络
论文链接:https://arxiv.org/abs/1907.04931
主要思路
:先采样子图,之后在子图上做完全连接的GCN。

通过在子图的GCN上添加归一化系数(通过预处理计算)来使得估计量无偏,Aggregation 的normalization为:

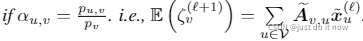
Loss的normalization为:
![]()
从而:

一个好的Samper应该使得:
1、相互具有较大影响的结点应该被sample到同一个子图;
2、每条边多有不可忽略的抽样概率。
设计Sampler减少评估的方差:
Random node sampler:
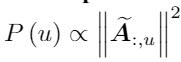
Random edge sampler:
![]()
Random walk based sampler:
![]()
4.部分实验


